
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes | Coding time: 9 minutes
A B-tree is a tree data structure that keeps data sorted and allows searches, insertions, and deletions in logarithmic amortized time. Unlike self-balancing binary search trees, it is optimized for systems that read and write large blocks of data. It is most commonly used in database and file systems.
B-Tree is a self-balanced search tree with multiple keys in every node and more than two children for every node. Basic properties associated with B-Tree:
- All the leaf nodes must be at same level.
- All nodes except root must have at least [m/2]-1 keys and maximum of m-1 keys.
- All non leaf nodes except root (i.e. all internal nodes) must have at least m/2 children.
- If the root node is a non leaf node, then it must have at least 2 children.
- A non leaf node with n-1 keys must have n number of children.
- All the key values within a node must be in Ascending Order.
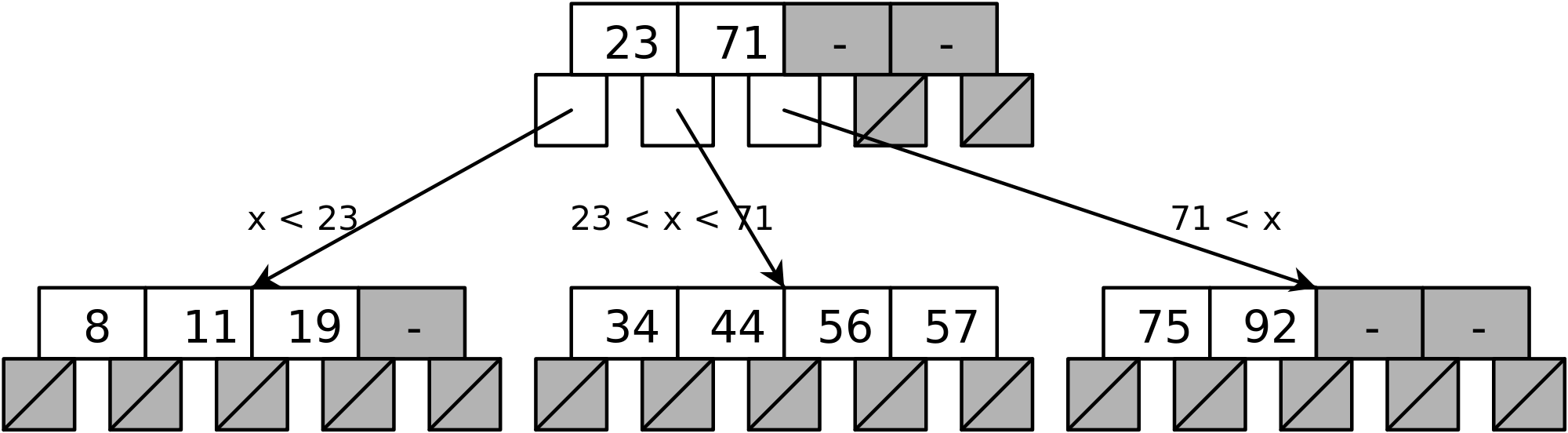
The figure depicts the basic construction of B-Tree.
Algorithm
- Basic operations associated with B-Tree:
-
Searching a node in a B-Tree
- Perform a binary search on the records in the current node.
- If a record with the search key is found, then return that record.
- If the current node is a leaf node and the key is not found, then report an unsuccessful search.
- Otherwise, follow the proper branch and repeat the process.
-
Insertion Operation of a node in a B-Tree depending on two cases:
- x is a leaf node. Then we find where k belongs in the array of keys, shift everything over to the left, and stick k in there.
-
x is not a leaf node:
- We can't just stick k in because it doesn't have any children; children are really only created when we split a node, so we don't get an unbalanced tree.
- We find a child of x where we can (recursively) insert k.
- We read that child in from disk. If that child is full, we split it and figure out which one k belongs in.
- Then we recursively insert k into this child (which we know is non-full, because if it were, we would have split it).
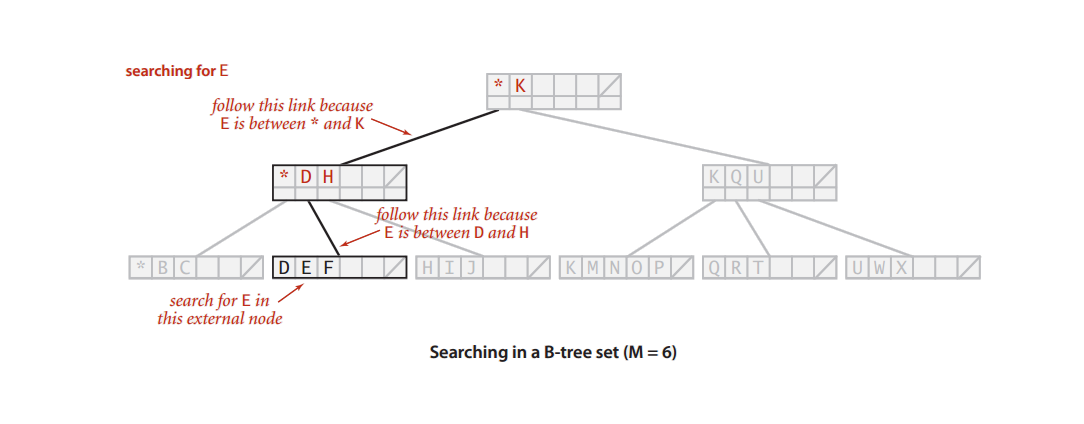
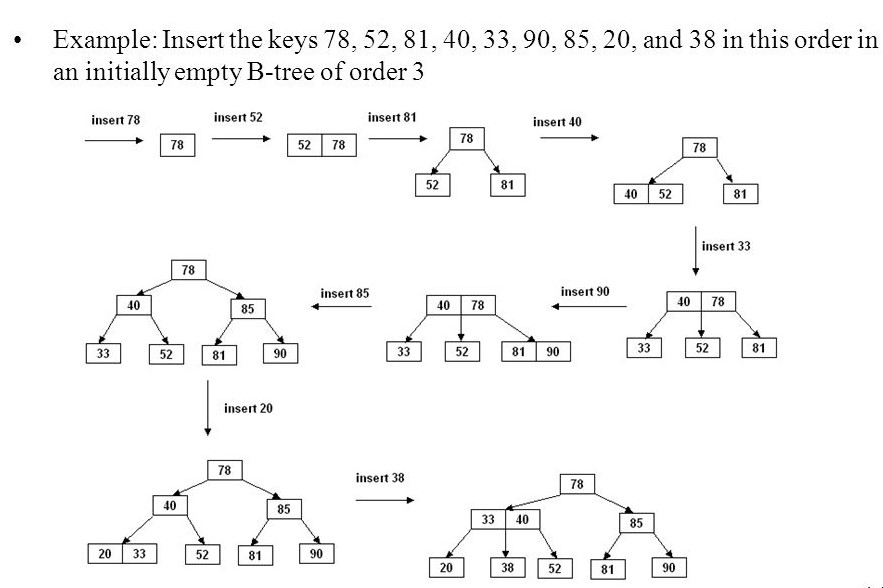
The figure illustrates the steps of insertion of an element in a B-Tree.
Complexity
-
Worst case search time complexity:
Θ(logn) -
Average case search time complexity:
Θ(logn) -
Best case search time complexity:
Θ(logn) -
Average case Space complexity:
Θ(n) -
Worst case Space complexity:
Θ(n)
Implementations
#include<stdio.h>
#include<conio.h>
#include<iostream>
using namespace std;
struct BTreeNode
{
int *data;
BTreeNode **child_ptr;
bool leaf;
int n;
}*root = NULL, *np = NULL, *x = NULL;
BTreeNode * init()
{
int i;
np = new BTreeNode;
np->data = new int[5];
np->child_ptr = new BTreeNode *[6];
np->leaf = true;
np->n = 0;
for (i = 0; i < 6; i++)
{
np->child_ptr[i] = NULL;
}
return np;
}
void searchOrTraverse(BTreeNode *p)
{
cout<<endl;
int i;
for (i = 0; i < p->n; i++)
{
if (p->leaf == false)
{
searchOrTraverse(p->child_ptr[i]);
}
cout << " " << p->data[i];
}
if (p->leaf == false)
{
searchOrTraverse(p->child_ptr[i]);
}
cout<<endl;
}
void sort(int *p, int n)
{
int i, j, temp;
for (i = 0; i < n; i++)
{
for (j = i; j <= n; j++)
{
if (p[i] > p[j])
{
temp = p[i];
p[i] = p[j];
p[j] = temp;
}
}
}
}
int childSplitOp(BTreeNode *x, int i)
{
int j, mid;
BTreeNode *np1, *np3, *y;
np3 = init();
np3->leaf = true;
if (i == -1)
{
mid = x->data[2];
x->data[2] = 0;
x->n--;
np1 = init();
np1->leaf = false;
x->leaf = true;
for (j = 3; j < 5; j++)
{
np3->data[j - 3] = x->data[j];
np3->child_ptr[j - 3] = x->child_ptr[j];
np3->n++;
x->data[j] = 0;
x->n--;
}
for (j = 0; j < 6; j++)
{
x->child_ptr[j] = NULL;
}
np1->data[0] = mid;
np1->child_ptr[np1->n] = x;
np1->child_ptr[np1->n + 1] = np3;
np1->n++;
root = np1;
}
else
{
y = x->child_ptr[i];
mid = y->data[2];
y->data[2] = 0;
y->n--;
for (j = 3; j < 5; j++)
{
np3->data[j - 3] = y->data[j];
np3->n++;
y->data[j] = 0;
y->n--;
}
x->child_ptr[i + 1] = y;
x->child_ptr[i + 1] = np3;
}
return mid;
}
void insertionOp(int a)
{
int i, temp;
x = root;
if (x == NULL)
{
root = init();
x = root;
}
else
{
if (x->leaf == true && x->n == 5)
{
temp = childSplitOp(x, -1);
x = root;
for (i = 0; i < (x->n); i++)
{
if ((a > x->data[i]) && (a < x->data[i + 1]))
{
i++;
break;
}
else if (a < x->data[0])
{
break;
}
else
{
continue;
}
}
x = x->child_ptr[i];
}
else
{
while (x->leaf == false)
{
for (i = 0; i < (x->n); i++)
{
if ((a > x->data[i]) && (a < x->data[i + 1]))
{
i++;
break;
}
else if (a < x->data[0])
{
break;
}
else
{
continue;
}
}
if ((x->child_ptr[i])->n == 5)
{
temp = childSplitOp(x, i);
x->data[x->n] = temp;
x->n++;
continue;
}
else
{
x = x->child_ptr[i];
}
}
}
}
x->data[x->n] = a;
sort(x->data, x->n);
x->n++;
}
int main()
{
int i, n, t;
cout<<"Please enter the number elements for insertion operation\n";
cin>>n;
for(i = 0; i < n; i++)
{
cout<<"Please enter the value\n";
cin>>t;
insertionOp(t);
}
cout<<"Traversing the constructed tree\n";
searchOrTraverse(root);
getch();
}
Applications
B-Tree has many important applications in computer science.
-
B-trees are preferred when decision points, called nodes, are on hard disk rather than in random-access memory (RAM)
-
B-trees save time by using nodes with many branches (called children), compared with binary trees, in which each node has only two children, thereby speeding up the process.
