
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 5 minutes
A binary tree is a tree (Data Structure) in which every node has at most 2 children i.e. the left child(left sub-tree) and the right child(right sub-tree). Node of a binary tree will look as follows:

From the figure you can see that a node consists of three parts.
- Pointer to left child
- Data
- Pointer to right child
Suppose there is a binary tree of height "h". Here height of root is considered as 0.
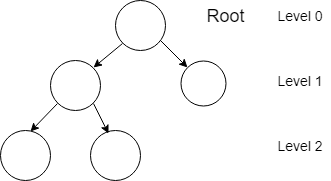
There are few properties of binary tree :
-
Parent of node i will be floor function of i/2, except the root node. Because root node has no parent. Taking an example, parent of node 2 will be 2/2 i.e. node 1, and also paremt of node 3 will be 1, floor function of 3/2.
-
The left child of node i will be 2i. For example, left child of node 3 will be 6. The right child of node i will be 2i+1. For example, right child of node 3 will be 7.
-
Maximum Number of nodes at any level "l".
In a binary tree every node has at most 2 childrens, maximum number of nodes at level "l" can be 2^(l-1).
For level = 1, maximum number of nodes will be 1. For level = 2, maximum number of nodes will be 2. For level = 3, maximum number of nodes will be 4 and so on... -
Maximum Number of nodes in a binary tree.
For maximum number of nodes in a tree, all levels will also have maximum number of nodes.
Let's take an example, let h = 2. So, for maximum number of nodes in a tree, there will be 1 node at height = 1. And there will be 2 nodes at hight = 2. So maximum number of nodes in a binary tree of height h would be 1+2+4+8+...+2^(h-1). Now sum of this series is 2^(h+1) - 1.
There are four types of binary trees.
- Complete Binary Tree : A Binary Tree is complete Binary Tree if all levels are completely filled except the last level. And last level should have all keys(data) as left as possible.
- Perfect Binary Tree : A Perfect Binary Tree is a binary tree in which all interior nodes have two children and all leaves have the same depth i.e same level.
- Full Binary Tree : A Full Binary Tree is a tree in which every node other than the leaves has two children.
- Balanced Binary Tree : A Balanced Binary Tree is a binary tree in which height of the tree is O(Log n) where n is the number of nodes.
Few Operations
- Insertion
Suppose a binary tree is given with few allocated values. As given tree is binary tree so we can insert element wherever we want. Only property of binary tree should be maintained. And property is that every node can have maximum two children.
So we need to insert the new element wherever we find the node whose left or right child is null.
Given :
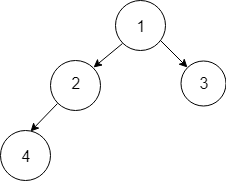
Inserting new element in given tree
Output :
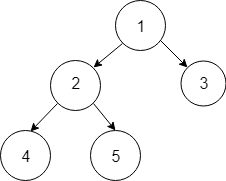
Code for inserting element is given in Pseudocode section.
- Deletion
For deletion, first we need to find the element which we want to delete. And as deletion is done in Binary Tree so replace that element with the right most node's data. And then delete the right most node.
Given Tree :
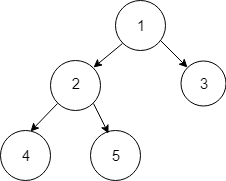
Delete data 3.
Deletion steps :
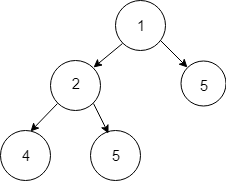
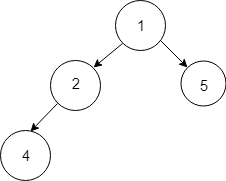
By thiss way deletion is done in binary trees. Code for deletion is given in Pseudocode section.
Pseudocode
- Example of code for generating a node in a tree.
struct node {
int data;
struct node *left;
struct node *right;
};
- Example of code for Insertion in a Binary Tree.
struct node * insertInBinaryTree(struct binaryTreeNode * root, int num)
{
struct node * temp = NULL;
struct queue * Q = NULL;
struct node * newNode = (struct binaryTreeNode *)malloc(sizeof(struct binaryTreeNode));
newNode -> data = num;
newNode -> left = NULL;
newNode -> right = NULL;
if(root == NULL) {
root = newNode;
return root;
}
Q = enQueue(Q, root);
while(!isQueueEmpty(Q)) {
temp = Q -> front -> data;
Q = deQueue(Q);
if(temp -> left != NULL)
Q = enQueue(Q, temp -> left);
else {
temp -> left = newNode;
free(Q);
return root;
}
if(temp -> right != NULL)
Q = enQueue(Q, temp -> right);
else {
temp -> right = newNode;
free(Q);
return root;
}
}
free(Q);
return root;
}
- Example of code for deleting a node from Tree.
void deletDeepest(struct Node *root,
struct Node *d_node) {
queue<struct Node*> q;
q.push(root);
struct Node* temp;
while(!q.empty()) {
temp = q.front();
q.pop();
if(temp == d_node) {
temp = NULL;
delete(d_node);
return;
}
if (temp->right) {
if (temp->right == d_node) {
temp->right = NULL;
delete(d_node);
return;
}
else
q.push(temp->right);
}
if (temp->left) {
if (temp->left == d_node) {
temp->left=NULL;
delete(d_node);
return;
}
else
q.push(temp->left);
}
}
}
void delete(struct Node* root, int key) {
queue<struct Node*> q;
q.push(root);
struct Node *temp;
struct Node *key_node = NULL;
while (!q.empty()) {
temp = q.front();
q.pop();
if (temp->key == key)
key_node = temp;
if (temp->left)
q.push(temp->left);
if (temp->right)
q.push(temp->right);
}
int x = temp->key;
deletDeepest(root, temp);
key_node->key = x;
}
Implementation
Example of code for generating a tree with 5 nodes.
struct node {
int data;
struct node *left;
struct node *right;
};
struct node * insertInBinaryTree(struct binaryTreeNode * root, int num)
{
struct node * temp = NULL;
struct queue * Q = NULL;
struct node * newNode = (struct binaryTreeNode *)malloc(sizeof(struct binaryTreeNode));
newNode -> data = num;
newNode -> left = NULL;
newNode -> right = NULL;
if(root == NULL) {
root = newNode;
return root;
}
Q = enQueue(Q, root);
while(!isQueueEmpty(Q)) {
temp = Q -> front -> data;
Q = deQueue(Q);
if(temp -> left != NULL)
Q = enQueue(Q, temp -> left);
else {
temp -> left = newNode;
free(Q);
return root;
}
if(temp -> right != NULL)
Q = enQueue(Q, temp -> right);
else {
temp -> right = newNode;
free(Q);
return root;
}
}
free(Q);
return root;
}
void deletDeepest(struct Node *root,
struct Node *d_node) {
queue<struct Node*> q;
q.push(root);
struct Node* temp;
while(!q.empty()) {
temp = q.front();
q.pop();
if(temp == d_node) {
temp = NULL;
delete(d_node);
return;
}
if (temp->right) {
if (temp->right == d_node) {
temp->right = NULL;
delete(d_node);
return;
}
else
q.push(temp->right);
}
if (temp->left) {
if (temp->left == d_node) {
temp->left=NULL;
delete(d_node);
return;
}
else
q.push(temp->left);
}
}
}
void delete(struct Node* root, int key) {
queue<struct Node*> q;
q.push(root);
struct Node *temp;
struct Node *key_node = NULL;
while (!q.empty()) {
temp = q.front();
q.pop();
if (temp->key == key)
key_node = temp;
if (temp->left)
q.push(temp->left);
if (temp->right)
q.push(temp->right);
}
int x = temp->key;
deletDeepest(root, temp);
key_node->key = x;
}
struct node* newNode(int data) {
struct node* node = (struct node*)malloc(sizeof(structnode));
node->data = data;
node->left = NULL;
node->right = NULL;
return(node);
}
int main()
{
struct node *tree = null;
struct node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
tree = insertInBinaryTree(root,6); // This will add new element (6) to existing tree
delete(tree,3) // This will delete element data 3 from existing tree
return 0;
}
Complexity
- Searching : For searching we need to traverse all elements so worst case complexity will be O(n).
- Insertion : Worst case complexity will be O(n).
- Deletion : Worst case complexity will be O(n).
Applications
- Manipulate hierarchical data
- Router algorithms
- Storing Router Tables
- Manipulate sorted lists of data
- As a workflow for compositing digital images for visual effects
- Form of a multi-stage decision-making
References
- Binary Tree
- Introduction to Algorithms, 3rd Edition by Thomas H. Cormen , Charles E. Leiserson, Ronald L. Rivest, Clifford Stein
