Wigderson Graph Colouring Algorithm in O(N+M) time

Reading time: 20 minutes | Coding time: 9 minutes

Wigderson Algorithm is a graph colouring algorithm to color any n-vertex 3-colorable graph with O(√n) colors, and more generally to color any k-colorable graph with $O(n^{1− (1/k−1)})$ colors.

The previous best upper bound on the number of colors needed for coloring 3-colorable n-vertex graphs in polynomial time was O(√n/√log n) colors by Berger and Rompel, improving a bound of O(√n) colors by Wigderson.

A k-coloring of a graph is an assignment of one of k distinct colors to each vertex in the graph so that no two adjacent vertices are given the same color. The chromatic number of a graph is the smallest k such that the graph can be k-colored. Graph coloring problems model a collection of scheduling problems such as examination scheduling and register allocation. Graph coloring is also closely related to other combinatorial problems such as finding the maximum independent set in a graph (the largest set of vertices such that no two have an edge between them). Unfortunately from the algorithmic point of view, as is well known, the problem of coloring a graph with the minimum number of colors is NP-hard, even restricted to graphs of constant chromatic number at least 3. Thus, researchers attempting to find good fast algorithms must consider issues of approximation .

Pseudocode

• Based on the following facts:
  • The subgraph induced by the neighborhood of any vertex is 2-colorable.
  • 2-coloring is polynomial time solvable.
  • ∆ + 1 colors suffice to color any graph having maximum degree ∆ .
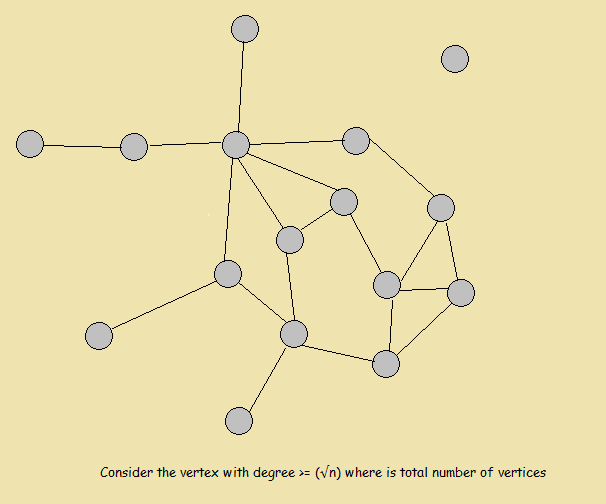
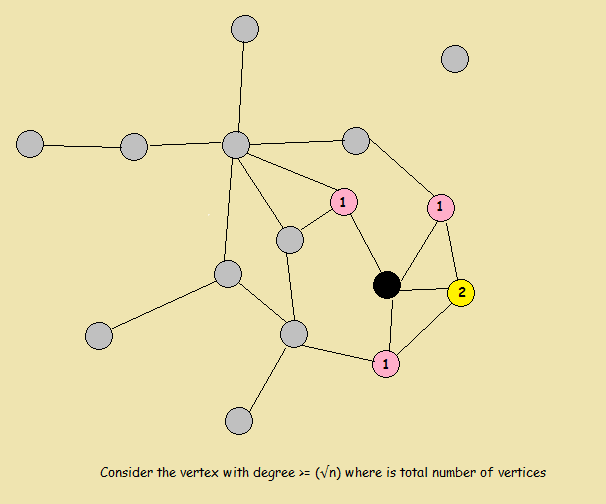
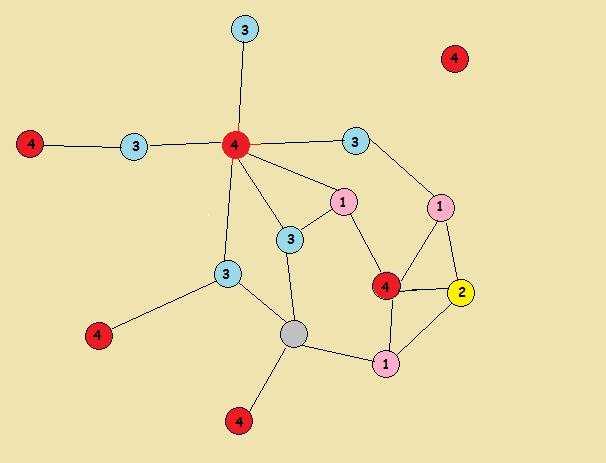
• Using facts 1 and 2, 2-color N(v) for a vertex v having deg(v) ≥ |√n| ; remove colored vertices and iterate.
• The remaining graph has ∆ < |√n|; color it using fact 3.
• Total number of colors used: O(√n)

Complexity

• The time complexity of algorithm is O(m + n) .

Applications

1. Making Schedule or Time Table: Suppose we want to make am exam schedule for a university. We have list different subjects and students enrolled in every subject. Many subjects would have common students (of same batch, some backlog students, etc). How do we schedule the exam so that no two exams with a common student are scheduled at same time? How many minimum time slots are needed to schedule all exams? This problem can be represented as a graph where every vertex is a subject and an edge between two vertices mean there is a common student. So this is a graph coloring problem where minimum number of time slots is equal to the chromatic number of the graph.

2. Mobile Radio Frequency Assignment: When frequencies are assigned to towers, frequencies assigned to all towers at the same location must be different. How to assign frequencies with this constraint? What is the minimum number of frequencies needed? This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other.

3. Sudoku: Sudoku is also a variation of Graph coloring problem where every cell represents a vertex. There is an edge between two vertices if they are in same row or same column or same block.

4. Register Allocation: In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers. This problem is also a graph coloring problem.

5. Bipartite Graphs: We can check if a graph is Bipartite or not by coloring the graph using two colors. If a given graph is 2-colorable, then it is Bipartite, otherwise not. See this for more details.

6. Map Coloring: Geographical maps of countries or states where no two adjacent cities cannot be assigned same color. Four colors are sufficient to color any map.

Further reading

First, get an overview of different approaches of the Graph Coloring problem: