Welsh Powell Algorithm for graph coloring in O(N^2) time

Reading time: 20 minutes | Coding time: 9 minutes

In graph theory, Welsh Powell is used to implement graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints.

In 1967 Welsh and Powell Algorithm introduced in an upper bound to the chromatic number of a graph . It provides a greedy algorithm that runs on a static graph.
The vertices are ordered according to their degrees, the resulting greedy coloring uses at most $max_i min{ d(x_i) + 1, i}$ colors, at most one more than the graph’s maximum degree. This heuristic is called the Welsh–Powell algorithm.

Pseudocode

Welsh Powell Algorithm:

• Find the degree of each vertex .
• List the vertices in order of descending valence i.e.valence degree(v(i)) >= degree(v(i+1)) .
• Colour the first vertex in the list.
• Go down the sorted list and color every vertex not connected to the colored vertices above the same color then cross out all colored vertices in the list.
• Repeat the process on the uncolored vertices with a new color-always working in descending order of degree until all in descending order of degree until all vertices are colored.

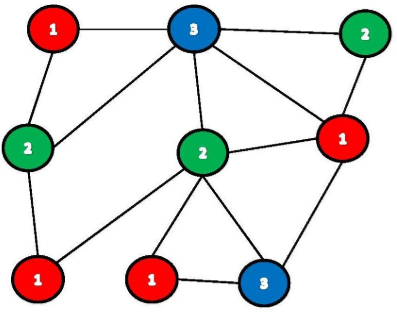
Example walk-through

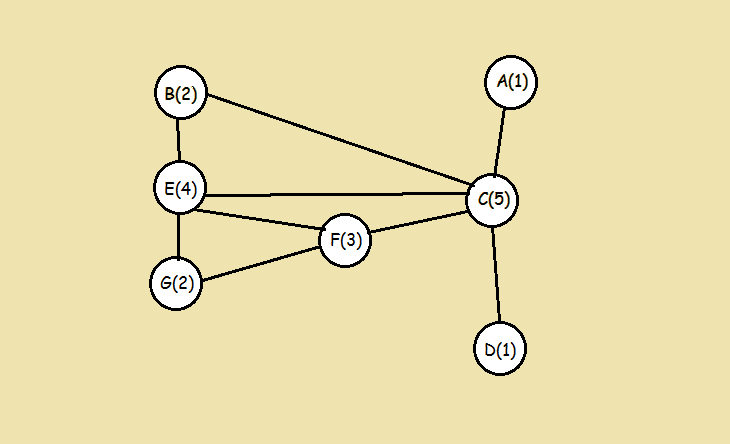
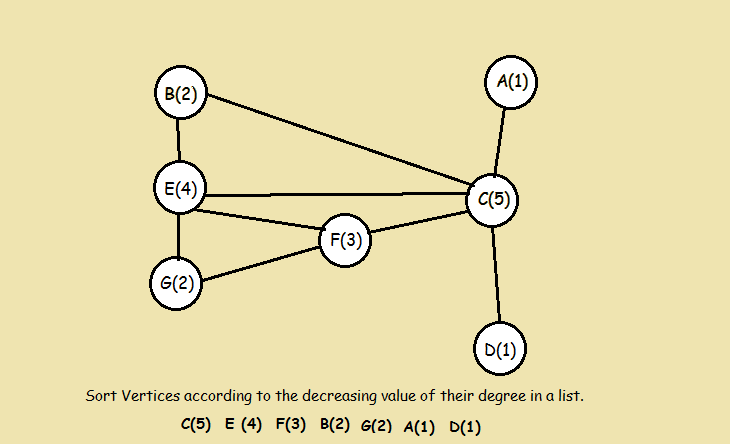
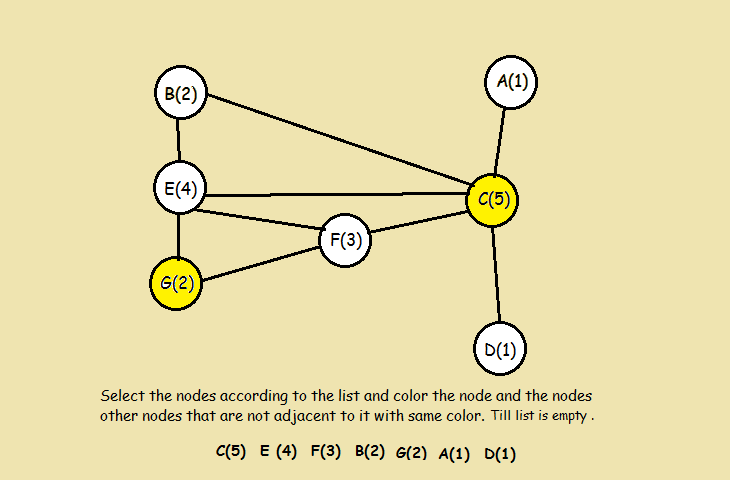
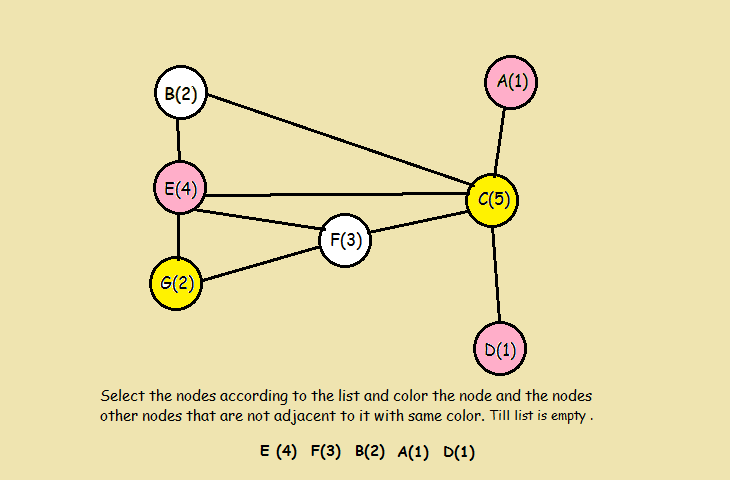
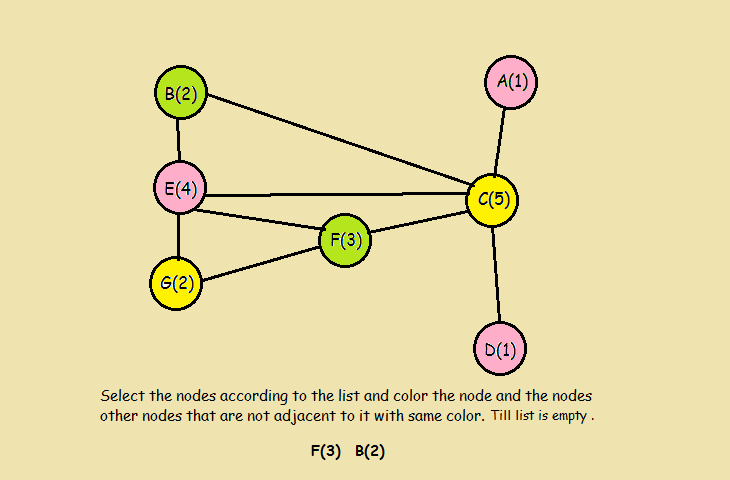
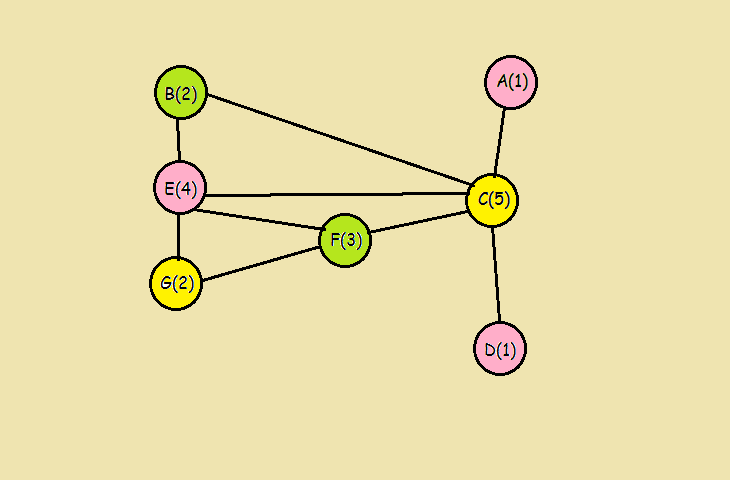
Implementations

Following is the C++ implementation of the Welsh Powell algorithm:

#include <iostream>
#include <algorithm>
#include <cstring>
const int x = 10;   //vertex no.
const int colors[x] = { 0,1,2,3,4,5,6,7,8,9 };
int counter = 0;
bool problem = false;
/*  Example graph
	 B      G---------J
	/ \      \        |
       /   \      \       |
      /     \      \      |
     A------C-------E-----K
     \     /       /      |
      \   /       /       |
       \ /       /        |
        D-------F---------L
*/
bool graf[x][x] = { //adj. matrix
	0,1,1,1,0,0,0,0,0,0,
	1,0,1,0,0,0,0,0,0,0,
	1,1,0,1,1,0,0,0,0,0,
	1,0,1,0,0,1,0,0,0,0,
	0,0,1,0,0,1,1,0,1,0,
	0,0,0,1,1,0,0,0,1,1,
	0,0,0,0,1,0,0,1,0,0,
	0,0,0,0,0,0,1,0,1,0,
	0,0,0,0,1,0,0,1,0,1,
	0,0,0,0,0,1,0,0,1,0
};
char vertex_names[x] = {'A','B','C','D','E','F','G','J','K','L'};
int rate_list[x]; //{ 0,0,0,0,0,0,0,0,0,0};
struct Graf 
{
	char vertex_id[x];
	int vertex_rates[x];
	bool adj[x][x];
	int colors[x];
	bool colored[x];
};
//welsh powell
void colorIt(Graf g) {
	counter++;
	int biggest=0;
	int temp_rate = 0;
	//rate listing from adj matrix (counting edges)
	if (counter == 1)
		for (int i = 0; i &lt; x; i++)
			for (int j = 0; j &lt; x; j++)
				if (g.adj[i][j])
					rate_list[i]++;
	for (int w = 0; w &lt; x; w++)
		if (!g.colored[w]) 
        {
			g.vertex_rates[w] = rate_list[w];
			if (temp_rate &lt; g.vertex_rates[w]) 
            {
				temp_rate = g.vertex_rates[w];
				biggest = w;
			}
		}
	//coloring biggest one first
	g.colors[biggest] = colors[counter];
	std::cout &lt;&lt; g.vertex_id[biggest] &lt;&lt;":color "&lt;&lt; g.colors[biggest]&lt;&lt;std::endl;
	//coloring which doesn't have path with biggest one
	for (int e=0;e &lt; x;e++)
		if (!g.adj[biggest][e] && biggest!=e && !g.colored[e]) 
        {
			for (int t = 0; t &lt; x;t++) 
            {
				if(g.adj[e][t] &&g.colors[t]==g.colors[biggest]) problem = true;
					if (t == x - 1 && !problem) 
                    {
						g.colors[e] = colors[counter];
						std::cout &lt;&lt; g.vertex_id[e] &lt;&lt;":color "&lt;&lt; g.colors[e] &lt;&lt; std::endl;
						g.colored[e] = true;
						problem = false;
					}
					else if (t == x - 1) problem = false;
			}
		}
		g.colored[biggest] = true;
	if (std::all_of(std::begin(g.colored), std::end(g.colored), [](bool i) { return i; })) {
		std::cout &lt;&lt; "Graph full colored" &lt;&lt; std::endl;
		system("pause");
		exit(EXIT_SUCCESS);
	}
	else colorIt(g); //recusive because too lazy to sort :)
}
int main()
{
	Graf graf1;
	//init color
	for (int y = 0; y &lt; x; y++) 
    {
		graf1.colors[y] = 99;
		graf1.colored[y] = false;
	}
	//init graph
	memcpy(&graf1.adj, &graf, sizeof(graf1.adj));
	memcpy(&graf1.vertex_id, &vertex_names, sizeof(graf1.vertex_id));
	colorIt(graf1);
	return 0;
}

Complexity

• The complexity of algorithm is $ O(N^2) $

Applications

1. Making Schedule or Time Table: Suppose we want to make am exam schedule for a university. We have list different subjects and students enrolled in every subject. Many subjects would have common students (of same batch, some backlog students, etc). How do we schedule the exam so that no two exams with a common student are scheduled at same time? How many minimum time slots are needed to schedule all exams? This problem can be represented as a graph where every vertex is a subject and an edge between two vertices mean there is a common student. So this is a graph coloring problem where minimum number of time slots is equal to the chromatic number of the graph.

2. Mobile Radio Frequency Assignment: When frequencies are assigned to towers, frequencies assigned to all towers at the same location must be different. How to assign frequencies with this constraint? What is the minimum number of frequencies needed? This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other.

3. Sudoku: Sudoku is also a variation of Graph coloring problem where every cell represents a vertex. There is an edge between two vertices if they are in same row or same column or same block.

4. Register Allocation: In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers. This problem is also a graph coloring problem.

5. Bipartite Graphs: We can check if a graph is Bipartite or not by coloring the graph using two colors. If a given graph is 2-colorable, then it is Bipartite, otherwise not. See this for more details.

6. Map Coloring: Geographical maps of countries or states where no two adjacent cities cannot be assigned same color. Four colors are sufficient to color any map.

Further reading

First, get an overview of different approaches of the Graph Coloring problem: