
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 15 minutes
A Bipartite Graph is one whose vertices can be divided into disjoint and independent sets, say U and V, such that every edge has one vertex in U and the other in V. The algorithm to determine whether a graph is bipartite or not uses the concept of graph colouring and BFS and finds it in O(V+E) time complexity on using an adjacency list and O(V^2) on using adjacency matrix.
Algorithm:
A bipartite graph is possible if it is possible to assign a colour to each vertex such that no two neighbour vertices are assigned the same colour. Only two colours can be used in this process.
Steps:
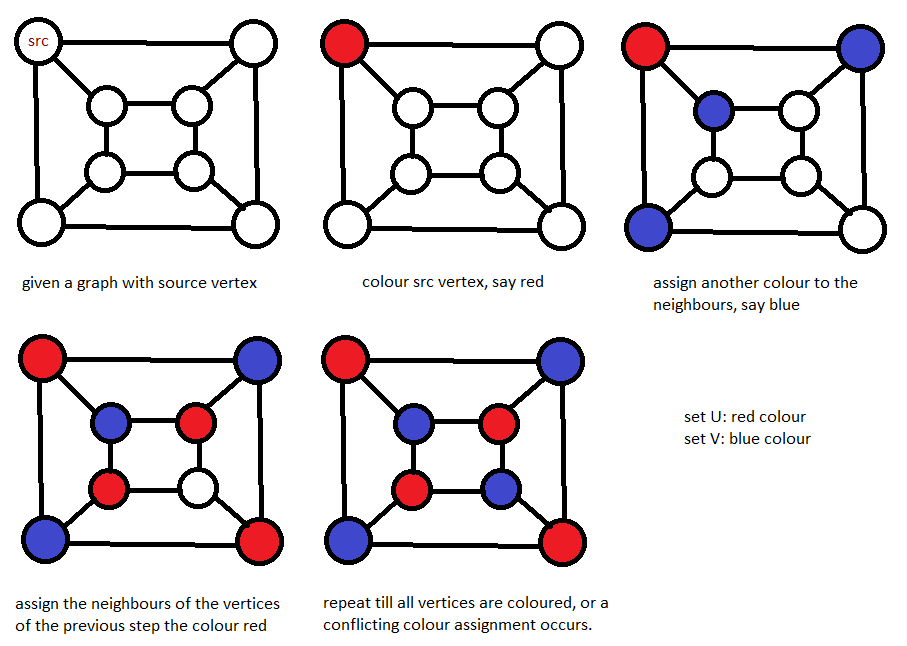
- Assign a colour(say red) to the source vertex.
- Assign all the neighbours of the above vertex another colour(say blue).
- Taking one neighbour at a time, assign all the neighbour's neighbours the colour red.
- Continue in this manner till all the vertices have been assigned a colour.
- If at any stage, we find a neighbour which has been assigned the same colour as that of the current vertex, stop the process. The graph cannot be coloured using two colours. Thus the graph is not bipartite.
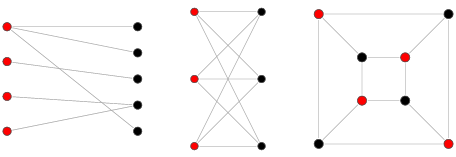
Example:
Psuedocode:
isBipartite(G,src){
Let q be an empty queue
s = src
colour v Red
q.enqueue(s)
while !q.empty()
u = q.dequeue()
for each v in u.adjList:
if v.color is nil:
v.color = (u.color == Red) ? Black : Red
q.enqueue(v)
elif v.color == u.color:
return "Not Bipartite"
return "Bipartite"
}
Complexity:
If Adjacency matrix is used, then:
Worst time complexity case: O(V^2)
Average time complexity case: O(V^2)
Best time complexity case: O(V^2)
Space complexity: O(V^2)
where V is the number of vertices.
In this algorithm, each vertex of the graph needs to be traversed once, and each neighbour of a vertex is traversed once. Since we are using an adjacency matrix, this results in a complexity of O(V^2).
If Adjacency list is used, then:
Worst time complexity case: O(V+E)
Average time complexity case: O(V+E)
Best time complexity case: O(V+E)
Space complexity: O(V+E)
where V is the number of vertices.
If we use adjacency list representation, this would result in a complexity of O(V+E) which is the cost of traversing the graph in this representation.
Implementation:
JAVA:
import java.util.Arrays;
import java.util.LinkedList;
public class GraphClient {
public static void main(String[] args) {
//adjacency matrix representation
int G[][] = { { 0, 1, 1, 1 }, { 1, 0, 1, 0 }, { 1, 1, 0, 1 }, { 1, 0, 1, 0 } };
System.out.println(isBipartite(G, 0));
}
public static boolean isBipartite(int[][] G, int src) {
//array to keep track of colours assigned to vertices
int[] colour = new int[G.length];
//0 = no colour; 1 = red; -1= blue
Arrays.fill(colour, 0);
LinkedList<Integer> queue = new LinkedList<>();
//keeps track of colour assigned
int curr = 1;
colour[src] = curr;
queue.addLast(src);
while (!queue.isEmpty()) {
int u = queue.removeFirst();
//if self-loop, return false
if (G[u][u] != 0)
return false;
//to give opposite colour to neighbour, update variable
curr = curr * -1;
//loop on neighbours
for (int v = 0; v < G.length; v++) {
//edge from u to v exists
if (G[u][v] != 0) {
//if neigbhour ahas same colour as vertex, not bipartite
if (colour[u] == colour[v])
return false;
else {
//assign other collour to neighbour
colour[v] = curr;
queue.addLast(v);
}
}
}
}
return true;
}
}
Applications:
-
Extensively used in coding theory. Bipartite graphs are used to decode codewords. Examples are Tanner graphs and Factor graphs
-
Bipartite graphs are also used to mathematically model common situations as well as serious problems like including cloud computing, big data, cognitive radio networks etc.
Question:
Can DFS be used to implement Bipartite Checking?
Further reading
First, get an overview of different approaches of the Graph Coloring problem:
Get an overview of Graph Coloring algorithmsLearn about a greedy approach for Graph Coloring
Understand Welsh Powell algorithm for Graph Coloring
Checking if a graph is bipartite using Graph Coloring and Breadth First Search
Learn about a Widgerson Algorithm for Graph Coloring
