Graph Coloring Greedy Algorithm [O(V^2 + E) time complexity]

Reading time: 15 minutes | Coding time: 9 minutes

In graph theory, graph coloring is a special case of graph labeling ; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form , it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color; this is called a vertex coloring. Similarly, an edge coloring assigns a color to each edge so that no two adjacent edges share the same color, and a face coloring of a planar graph assigns a color to each face or region so that no two faces that share a boundary have the same color.

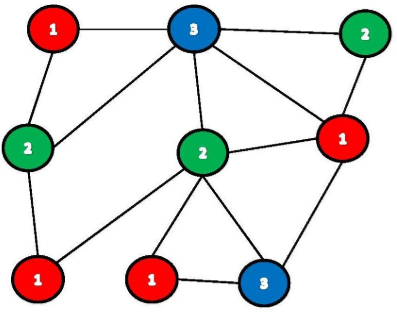
Chromatic Number: The smallest number of colors needed to color a graph G is called its chromatic number. For example, the following can be colored minimum 3 colors.

Vertex coloring is the starting point of the subject, and other coloring problems can be transformed into a vertex version. For example, an edge coloring of a graph is just a vertex coloring of its line graph, and a face coloring of a plane graph is just a vertex coloring of its dual. However, non-vertex coloring problems are often stated and studied as is. That is partly for perspective, and partly because some problems are best studied in non-vertex form, as for instance is edge coloring .

Origin

The convention of using colors originates from coloring the countries of a map, where each face is literally colored. This was generalized to coloring the faces of a graph embedded in the plane. By planar duality it became coloring the vertices, and in this form it generalizes to all graphs. In mathematical and computer representations, it is typical to use the first few positive or non negative integers as the "colors". In general, one can use any finite set as the "color set". The nature of the coloring problem depends on the number of colors but not on what they are.

Pseudocode

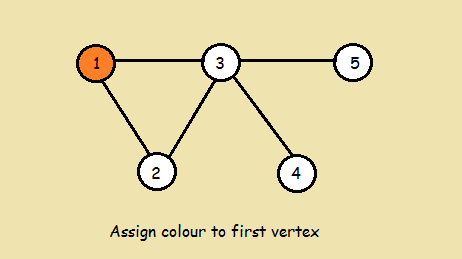
• Color first vertex with first colour.

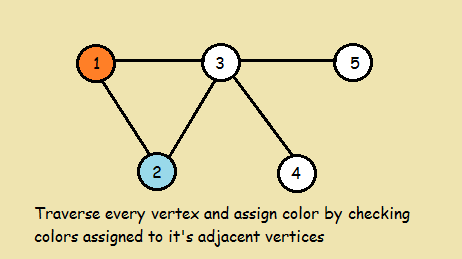
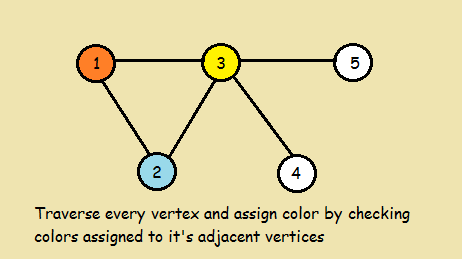
• Do following for remaining V-1 vertices

  Consider the currently picked vertex
  Colour it with the lowest numbered colour
  that has not been used on any previously colored vertices
  adjacent to it

  If all previously used colors appear on vertices adjacent to v, assign a new color to it .

Example

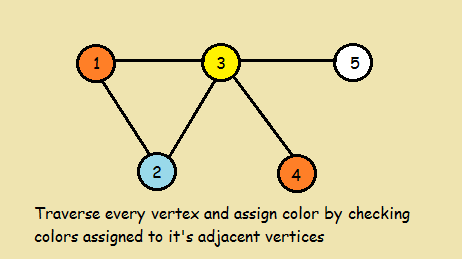
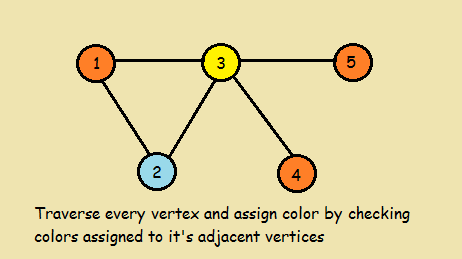
Implementations

#include <iostream>
#include <list>
using namespace std;
 
// A class that represents an undirected graph
class Graph
{
    int V;    // No. of vertices
    list<int> *adj;    // A dynamic array of adjacency lists
public:
    // Constructor and destructor
    Graph(int V)   { this->V = V; adj = new list<int>[V]; }
    ~Graph()       { delete [] adj; }
 
    // function to add an edge to graph
    void addEdge(int v, int w);
 
    // Prints greedy coloring of the vertices
    void greedyColoring();
};
 
void Graph::addEdge(int v, int w)
{
    adj[v].push_back(w);
    adj[w].push_back(v);  // Note: the graph is undirected
}
 
// Assigns colors (starting from 0) to all vertices and prints
// the assignment of colors
void Graph::greedyColoring()
{
    int result[V];
 
    // Assign the first color to first vertex
    result[0]  = 0;
 
    // Initialize remaining V-1 vertices as unassigned
    for (int u = 1; u < V; u++)
        result[u] = -1;  // no color is assigned to u
 
    // A temporary array to store the available colors. True
    // value of available[cr] would mean that the color cr is
    // assigned to one of its adjacent vertices
    bool available[V];
    for (int cr = 0; cr < V; cr++)
        available[cr] = false;
 
    // Assign colors to remaining V-1 vertices
    for (int u = 1; u < V; u++)
    {
        // Process all adjacent vertices and flag their colors
        // as unavailable
        list<int>::iterator i;
        for (i = adj[u].begin(); i != adj[u].end(); ++i)
            if (result[*i] != -1)
                available[result[*i]] = true;
 
        // Find the first available color
        int cr;
        for (cr = 0; cr < V; cr++)
            if (available[cr] == false)
                break;
 
        result[u] = cr; // Assign the found color
 
        // Reset the values back to false for the next iteration
        for (i = adj[u].begin(); i != adj[u].end(); ++i)
            if (result[*i] != -1)
                available[result[*i]] = false;
    }
 
    // print the result
    for (int u = 0; u < V; u++)
        cout << "Vertex " << u << " --->  Color "
             << result[u] << endl;
}
 
// Driver program to test above function
int main()
{
    Graph g1(5);
    g1.addEdge(0, 1);
    g1.addEdge(0, 2);
    g1.addEdge(1, 2);
    g1.addEdge(1, 3);
    g1.addEdge(2, 3);
    g1.addEdge(3, 4);
    cout << "Coloring of graph 1 \n";
    g1.greedyColoring();
 
    Graph g2(5);
    g2.addEdge(0, 1);
    g2.addEdge(0, 2);
    g2.addEdge(1, 2);
    g2.addEdge(1, 4);
    g2.addEdge(2, 4);
    g2.addEdge(4, 3);
    cout << "\nColoring of graph 2 \n";
    g2.greedyColoring();
 
    return 0;
}

Complexity

• O(V^2 + E) in worst case.(where V is the vertex and E is the edge).

Applications

1. Making Schedule or Time Table: Suppose we want to make am exam schedule for a university. We have list different subjects and students enrolled in every subject. Many subjects would have common students (of same batch, some backlog students, etc). How do we schedule the exam so that no two exams with a common student are scheduled at same time? How many minimum time slots are needed to schedule all exams? This problem can be represented as a graph where every vertex is a subject and an edge between two vertices mean there is a common student. So this is a graph coloring problem where minimum number of time slots is equal to the chromatic number of the graph.

2. Mobile Radio Frequency Assignment: When frequencies are assigned to towers, frequencies assigned to all towers at the same location must be different. How to assign frequencies with this constraint? What is the minimum number of frequencies needed? This problem is also an instance of graph coloring problem where every tower represents a vertex and an edge between two towers represents that they are in range of each other.

3. Sudoku: Sudoku is also a variation of Graph coloring problem where every cell represents a vertex. There is an edge between two vertices if they are in same row or same column or same block.

4. Register Allocation: In compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers. This problem is also a graph coloring problem.

5. Bipartite Graphs: We can check if a graph is Bipartite or not by coloring the graph using two colors. If a given graph is 2-colorable, then it is Bipartite, otherwise not. See this for more details.

6. Map Coloring: Geographical maps of countries or states where no two adjacent cities cannot be assigned same color. Four colors are sufficient to color any map.

Further reading

First, get an overview of different approaches of the Graph Coloring problem: