
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we will understand what fitting shelves problem is and will see a greedy approach algorithm of solving this problem.
What does Fitting Shelves Problem say?
So, the problem states that given a wall having length W, and two shelves of length m, and n, we are tasked with fitting the wall of length W with shelves of length m and n in such a way that the space left empty(which can't be filled with shelf) is to be minimized, and if possible the solution having larger number of longer shelves is to be preferred as longer shelf is the cheaper one, but cost is still secondary in our adventure of minimising the cost, we should be more worried abou how to minimise the empty space(if possible it should be zero).
For e.g.:- Suppose there is a wall of length 24, with two shelves of length 5 and 3, we need to minimize the empty space on the wall and if possible we should also try to minimize the cost(but that is secondary).
With intelligent guessing(as we don't have any algorithm yet), we can see that either we can fill the shelf with 8 shelves of length 3 each, or we can use 3 shelves of length 5 and 3 shelves of length 3, thus, totalling 6 shelves.
Hence, our solution according to the problem statement for this problem would be using 3 shelves of length 5 and 3 shelves of length 3, as it will minimze the empty space(no space would be left), also it will minimize the cost as we are using more number of longer shelves which are cheaper.
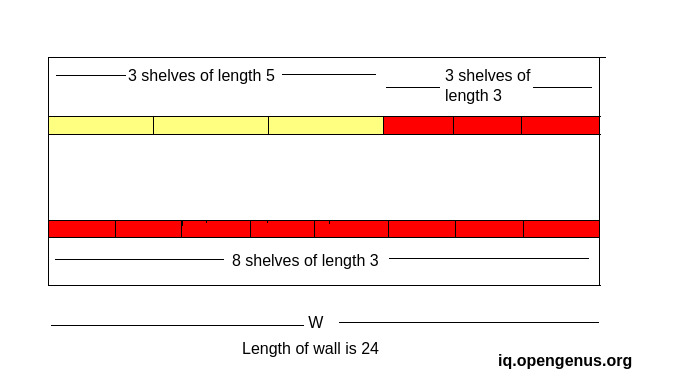
Brute force method for Fitting Shelves Problem
One method of solving fitting shelves problem can be that we form an equation in 2 variable and then trying every combination of values till we get our preferred solution.
For e.g.:- Suppose, we have a wall of length 31 and two shelves of length 6 and 3 each, we need to find solution for the fitting shelves problem for this wall.
Using brute force method:-
Let the number of shelves required of length 6 be x and let the number of shelves required of length 3 be y, then, for the optimal solution total length of shelves would be 6x + 3y , and we would have to try every combination of x and y values and then find the empty space for every combination to find our optimal solution.
Inputs to the values of x and y would only be integers and would be in the range of 0<=x<=(int) 31/6; and 0<= y <= (int) 31/3, which is the same as
0<=x<=5; 0<=y<=10.
Thus, we would have to try 50 combinations to get optimal solution for this problem.
Or, in other words total number of combinations to be tried is O((W^2)/(mn)).
Thus, we need to develop a less resource consuming algorithm to solve the same problem.
Greedy Algorithm for Fitting Shelves Problem
In greedy algorithm, we either try to minimise, or maximise certain quantity at each and every stage. Here, we will be trying to minimze the empty space on the wall at every stage ,and store it in a counter variable which will be used to keep track of the minimum empty space along with counter variables for correspnding number of shelves of length m and n used. And, we will then iterate according to the greedy algorithm steps mentioned below to achieve the desired solution.
Greedy Algorithm steps for Fitting Shelves Problem is mentioned below:-
1.In Greedy approach along with the constraint of the problem which states that larger shelf costs less than the smaller one, we start from 0, and we increase the no of longer shelves till no more longer shelves can be fit.
2.For each iteration, we find the empty space in that iteration, and we compare it with the least emoty space till that iteration, if the value at that stage is lesser than the one before that stage, we update the least empty space,
3.If least empty space is same in two cases, then we will update the least empty space only if it has more number of larger shelves,the value of least empty space at the end of the iteration will be our solution, along with corresponding number of larger length shelves and smaller length shelves.
Implementation:-
#include<iostream>
using namespace std;
void Fitting_shelf(int wall_length, int smaller, int larger)
{
// Output variables
int smaller_used = 0, larger_used = 0, min_empty = wall_length;
// p and q are no of shelves of smaller length and larger length respectively.
// remaining_length is the length which can't be filled in this iteration.
int p;
int q = -1; //For sake of programming simplicity, it has been declared as -1.
int remaining_length;
while (wall_length >= larger)
{
// place one more shelf of larger length
q += 1;
if(q>0)
wall_length = wall_length - larger;
//As many shelves of smaller length are to be placed till no more smaller length ones can be placed.
p = wall_length / smaller;
remaining_length = wall_length % smaller;
//Output variables are to be updated if remaining_length is lesser than previous least empty space.
if (remaining_length <= min_empty)
{
smaller_used = p;
larger_used = q;
min_empty = remaining_length;
}
}
cout<<"Number of smaller length shelf used is"<<smaller_used<<endl;
cout<<"Number of larger length shelf used is"<<larger_used<<endl;
cout<<"Least empty space or the corresponding number of shelves is"<<min_empty<<endl;
}
int main()
{
int wall,smaller,larger;
cout<<"Enter the length of the wall";
cin>>wall;
cout<<"Enter the length of the smaller shelf";
cin>>smaller;
cout<<"Enter the length of the larger shelf";
cin>>larger;
Fitting_shelf(wall,smaller,larger);
return 0;
}
Complexity of code:-
Space complexity is constant as total amount of space allocated is constant, and does not depend upon the input.
Thus, space complexity is O(1).
Since, the loop runs for Wall_length/Length of larger shelf times, thus, time complexity of this code is O(Wall_length/Length_of_largershelf).
Question
If the length of the wall is 34 with length of shelves being 5 and 8 find the minimum empty space using fitting shelves algorithm
With this article at OpenGenus, you must have the complete idea of Fitting Shelves Problem.
