Hashing in Blockchain
In this article, we learn about hashing functions, the hash rate, hashing requirements simple, and Merkle tree hashing in relation to blockchain technologies.
Table of Contents.
- Introduction.
- Hash Function.
- Hash Rate.
- Hashing Requirements.
- Simple Hashing.
- Merkel Tree Hashing.
- Summary.
- References.
Prerequisite.
Introduction
As we learned in the prerequisite article, there exist three major types of cryptography, symmetric, asymmetric and cryptographic hashing. The first we said is not safe since it's faced with issues such as risky key transfer and the same key being used to encrypt and decrypt. The second type was an improvement of the first, here we have two keys, the public, and private keys, the former is shared and anyone can know it, it is accompanied by a private key which should be kept private, together they form a pair. Both are used to encrypt(sender's private + receiver's public) and decrypt(receive's private key + sender's public key). This is safe however, one can lose the private key to malicious users. The final which will be our topic of discussion is cryptographic hashing, here any amount of text could be a whole 10000-page book, the whole internet an application if passed through a hash function to generate a fixed size hash. This hash is irreversible. Once generated it is very hard to decipher the original text. As we shall come to learn this is commonly used in blockchains.
Encryption is fundamental to participating in a blockchain, just like a password is needed to hold funds in a bank account. It is used to secure transactions and funds and the data integrity on the blockchain.
Hash Function.
A hash function is just like a function in a program that is used to map data to an arbitrary size of fixed-size values. Hash functions reduce any length of text into a fixed size of irreversible hash. Commonly used hash functions include; MD5, SHA-3, and SHA-256, for more on this, check out this article.
Bitcoin uses SHA-256 while Etherium uses Keccak-256. Hashes generated by these algorithms are very hard to crack and if one does embark on this journey, he/she will have to try out 2 ^ 256 combinations, considering the computing power at our disposal is not realistic.
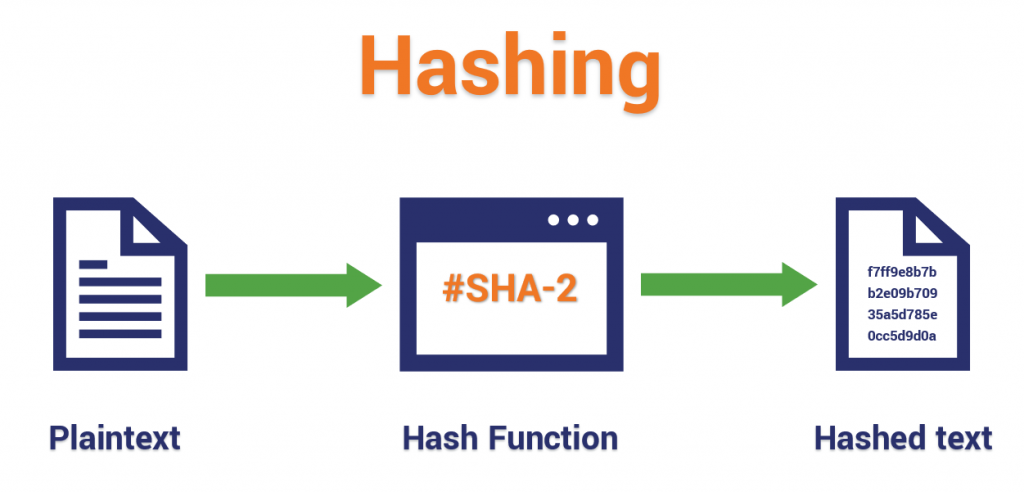
A slight modification of input will lead to a very different hash every time. When data produces the same hash, this is referred to as a collision. It is very rare but occurs, it is solved using other techniques such as chaining. This is covered here
Steps involved in SHA-256 hashing
- We start by adding some extra bits to the message such that the length is 64 bits, a multiple of 5125. The first bit to be added is one followed by 0s.
- We then add 64 bits of data to create a plain text multiple of 512 and calculate the 64-bits of characters by applying the modulus to the original text without the padding.
- We then initialize default values for eight buffers to be used in the rounds. We also store 64 different keys in an array from arr[0] - arr[63].
- We break down the message into 512-bit blocks and put each block through 64 rounds of operations whereby the output of a block serves as the input for the following block.
- The above cycle repeats itself until we reach the last 512-bit block. We then take the output as the final hash digest. This digest will be a 256-bit length digest.
To test this practically, refer to the link provided in the references section.
Steps involved in Keccack hashing
Keccack is a sponge function that operates on a finite state by iteratively applying the inner permutation to it, interleaved with the entry of input or the retrieval of output. The steps involved in this algorithm are as follows;
- Just like we did for the SHA-256 algorithm, we pad the message starting with 1 followed by 0s, however, in this case, we end the padding with 1. ie. 10...1. The final length of the message is a multiple of the bitrate of the function. We then divide the message into r-bit blocks where r is the bitrate(1088).
- The next phase is the absorbing phase. Here we initialize a state size(S). We then process the message blocks as follows, for each block, we pad it such that the total length of the block is b bits(1600) where b = bitrate + capacity(512). We then XOR the output with state S and pass the result to a permutation function. We repeat the process for the rest of the blocks.
- The final phase is referred to as the squeezing phase. Here we get the first r bits of the state from the previous step, we call this X. If the length of the X is greater than the output length, then we have our hash value for the input message as the first n bits of X where n is 256.
For an in-depth guide to this algorithm, more can be found on the link provided in the references section.
Hash Rate.
This is how fast or slow hashing is. The total computational power used by the proof of work algorithm to process transactions of the blockchain. As mentioned earlier, hashing consumes a lot of computational power, especially if you are on the offensive trying to crack one. In blockchain technology, a high hash rate is a good sign as it is an indication of more miners verifying transactions, a higher hash rate higher block difficulty, and more network security. We measure the hash rate by the # of calculations per second. It can be Kh/s, MH/s, GH/s... and so on.
As mentioned in earlier articles, miners compete to solve a puzzle specified by the blockchain, the winner is awarded an incentive for efforts put in. This means, that to be a competitive miner, one needs a computer that can perform a lot of calculations fast.
Hash rate is a factor for determining network security, as the higher, it is, the more participants, the more immutability and security. For anyone to have centralized control of the network, he/she needs to control 51% of the network, this is one of the threats to a blockchain - a 51% attack
Hash rate can also be an indication of the cryptocurrency markets, when it's high, the market is bullish, when low, the market is bearish, this is because miners have stopped mining or maintaining the network since rewards are no longer appealing in the current market state.
Hashing Requirements.
A hash function should fulfill the following criteria;
- It should apply to any block of data
- It should be easy to compute
- It should produce fixed-size length output for any input
- Given a block s, it should be computationally infeasible to find y != x with H(y) = H(x) - one-way property. This means that nobody should be able to get the original message from the hash.
- It should be impossible to find a pair(x, y) such that H(x) = H(y) - collision resistance - no two inputs produce the same hash.
These are achieved by using a good algorithm and using a large number of bits for the hash value. The commonly used size is 256 bits for the SHA-3, SHA-256, Keccak algorithm. Here a hacker would have to try 2 ^ 256 combinations. This is also how rare collisions are.
Now we compare two hashing techniques based on the data arrangement, the first simple hashing hashes data linearly while the second stores data in a tree structure.
Simple Hashing.
In this type of hashing, data or input is linearly hashed. Data is arranged in a line and then hashed.
This type of hashing is used when we have a fixed number of items to hash e.g a block header or we want to verify a composite block's integrity.
Note that here we are dealing with the whole block rather than individual block items(transactions).
Merkel Tree Hashing.
A Merkel tree is a data structure with hashes of different blocks which summarize all block transactions with s single root hash.
Unlike simple hashing where data is linearly hashed, data is structured in a tree as leaf nodes, these leaf nodes are combined pair-wise and additionally hashed using simple hashing. In this case, if any leaf node has corrupt data, it is easily detectable because it is compared to the root node, which is collectively generated by the original leaves of the tree.
The following is a demonstration of the Merkel tree hashing algorithm used on Ethereum.
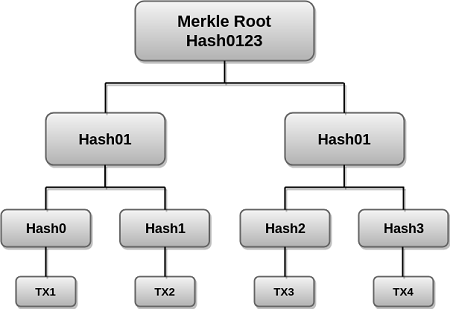
Above we have 4 transactions, each with data, they pass through a hash function and we have hashes, the 4 hashes are combined into two hashes which are then combined into a single hash, this completes the tree. Now, if any transaction is corrupted at any point in time, the root node hash won't match.
The root of the Merkel tree is stored in the block header, the bitcoin block that is hashed during mining. This block header contains the hash of its predecessor, a nouce, and the root hash of all transactions within the block.
Pros of using the Merkel tree include;
- Data integrity and validity.
- Hashing saves a lot of disk space, this is why it is also used in data storage platforms such as dropbox.
Summary
Simple hashing is used when we have a fixed number of items to hash while Merkel tree hashing is used when items differ from block to block, items such as transactions, states, and receipts.
The state variable can be modified by the execution of a smart contract, the result can be returned in a receipt.
Ethereum hashing functions are used to generate, account addresses, digital signatures, transaction hashes, state hashes, receipt hashes, and block header hash.
SHA-3, SHA-256, and keccak algorithms are used for hashing it bitcoin and Ethereum blockchains.