In this article, we discuss hash tables and their implementations on a larger scale while maintaining its computational complexity that is Distributed Hash Table.

Table of contents:

1. Introduction to Hash Table
   • Chaining
   • Open Addressing
   • Universal Hashing
   • Steps
2. Distributed Hash Tables
   • Properties of DHTs
   • Problem
   • Naive Solution
   • Drawbacks
   • Optimized implementation
   • Problem
   • Solution
3. Practical Applications of Distributed Hash Tables

Prerequisite: Hash Map / Hash Table

Introduction to Hash Table

A hash table is a data structure that stores data in an associative manner. Associative meaning each data value in the table is mapped onto a unique index value.
Access is fast knowing the index of the data.

We can also define a hash table as an implementation of a set or a map using hashing.

Set:

• Unordered_set in C++.
• HashSet in Java.
• Set in python.

Map:

• Unordered_map in C++.
• HashMap in Java.
• Dict in python.

Hashing is a technique used to convert large sized data into small manageable keys by use of hash functions.

A hash function is a mathematical function that is used to map keys to integers.

An element is converted into a small integer by using a hash function.
The small integer will be used as the key for the original element value in th hash table.

Note: The speed of a hash table depends on the choice of hash function.

Properties of a good hash function.

• Deterministic.
• Fast to compute.
• Offers good key distribution.
• Fewer collisions.

There are no ways to assure some of the above conditions since the probability distribution from which keys are drawn from is unknown.

Collisions are a common problem encountered in hashing, that is, when two keys are hashed onto the same index in a hash table
.
This problem is resolved using chaining, open addressing or use of a universal family.

Chaining

This is where each index in the hash table will have a linked list of elements, elements that compute to same hash value will be chained together in the same index.
Note: A good hash function is still important because we could encounter a case where we have very long chains on one index and no chain in others. We need to keep chains at least balanced because to reach an element in a chain we have to traverse the linked list.

Open Addressing

Also called closed hashing is whereby a hash table is maintained as an array of elements(not buckets), each index is initialized to null.
To insert we check if the desired position is empty if so we insert an element otherwise we find another place int the array to insert it.
In this approach, collisions are solved by probing, that is, searching for an alternative position in the array. Probing sequences are used here. You can learn more about probing sequences in the links at the end of this post.

Universal Hashing

For any deterministic hash function there is a bad input for which there will be a lot of collisions which will lead to O(n) time for access.
In universal hashing, we choose a random hashing function from a family of hash functions that is independent of the keys that will be stored. This will yield good performance no matter the inputs.

Steps

1. We define a universal family, a set of hash functions whereby any two keys in the universe have a small probability of collision.
2. We select random hash functions from the set of deterministic hash functions and use it throughout the algorithm.
   Note: By cleverly randomizing choice of hash function at run time, we guarantee a good average case running time.
   You can read more on this in the links at the end of this post.

Distributed Hash Tables

This is a distributed system that provides lookups similar to hash tables on a larger scale.
Distributed hash tables store big data on many computers and provide fast access as if it was on a single computer.
It does this by use of nodes which are distributed across the network.
To find a node that "owns" an object we hash the object using a hash function which will give a value that represents the node in a cluster.
In effect the hash table buckets are now independent nodes in a network.

Properties of DHTs

1. Fault tolerance - when a node fails, its data is inherited.
2. Reliability - nodes fail and new ones are added.
3. Performance - fast retrieval of information on a larger scale.
4. Scalability - functions even with multiple nodes being added to it.
5. Decentralized - nodes form a system but each act independently.

Problem

We need to store trillions of objects or even more considering data that gets generated these days.
We also need fast search/lookup once we store this huge amount of data.
We consider a hash table data structure for this case, which provides constant time O(1) lookups, however in this case we are talking about big data whose storage requirements are much larger, n = ${10}^{12}$, the memory requirements become too much and the computational complexity will deteroriate.

Naive Solution

Lets say we get 1000 computers.
We need to store a dictionary of key-value pairs (k1, v1), (k2, v2) across these cluster of computers in a way that is easy to manipulate the data without having to think about the details.
Create a hash table on each of them for storing these objects.
We use a hash function to determine which computer "owns" a particular object, h(O) mod 1000, this will give a number from 0 - 999 which will represent a particular computer in the cluster which owns the object.
When a search/modify request is sent from the client, the hash function is computed and sent to the computer that owns the resource.

Drawbacks

1. Computers break occasionally and even if we store several copies of the data of one computer, we need to relocate data from the broken to a new computer.
2. As the data grows we need more computers and when we add more to the existing cluster, the previous hash function h(O) mod 1000 no longer works when we need to redistribute keys.

Optimized implementation

We introduce the concept of consistent hashing.
Consistent hashing is one way to determine which computer stores the requested object.
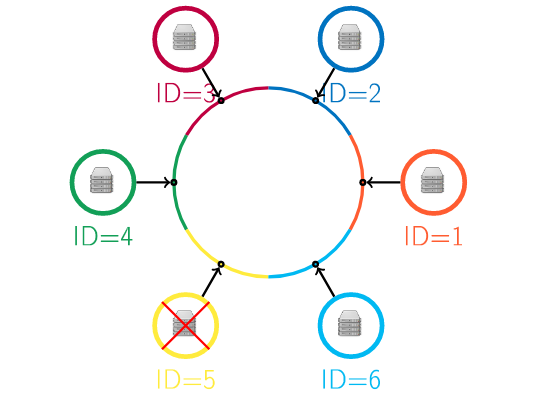
We choose a hash function h with a cardinality m and place points clockwise from 0 - m-1 forming a circle.
Each object and computer in the network will be mapped onto this circle using a universal hash function, that is, h(O) and h(computerId).
Each object mapped onto the circle will be stored by the computer within the same arc as the object.
Each computer will store all objects falling on the same arc in the circle.

When a computer in the cluster fails, its neighbors will inherit its data.
When a new computer is added to the cluster, its hash value is computed and it is placed in the circle, based on its position in the circle, it will inherit data from its neighbors.

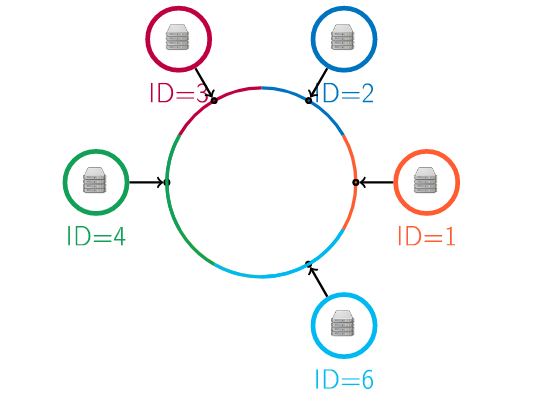
Problem

When a computer breaks, we need a well defined strategy for relocating the data.
A node needs to know where to send its data.

Solution

Overlay network, each node will store addresses of its immediate neighbors and its neighbors of neighbors in distance powers of 2, that is, 1 -> 2 -> 4 -> 8 -> 16

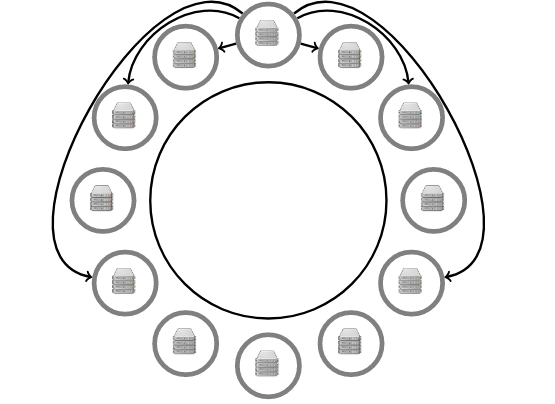
For each key, each node will either store it or know some closer node to this key. When a request for a key is sent to a node in the network, the node will either have the key or it will redirect the request to another node in the network which is closer to this key, these iterations will continue until the request reaches a node that stores the key.

It takes log(n) number of steps to reach the node that actually stores the key.
This is known as an overlay network, a network of nodes that know some other neighbor nodes, we use it to route data to and from nodes within a network of nodes.

Practical Applications of Distributed Hash Tables

1. Distributed storage, dropbox, yandex disk.
2. Blockchains.

Questions

How is a distributed hash table implemented in a distributed storage system such as dropbox to achieve instant uploads and storage optimizations?

References

Hash Tables - Chapter III section 11 in [CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms.