What is a Minimum Spanning Tree?

• Description
• Properties
• Applications
• Discussions

Reading time: 15 minutes

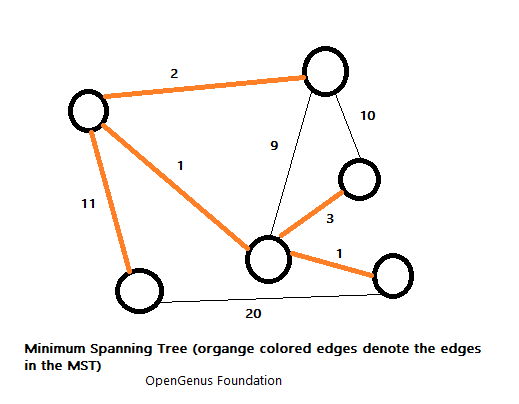
A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted directed or undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. It is a spanning tree whose sum of edge weights is as small as possible.

More generally, any edge-weighted undirected graph (not necessarily connected) has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.

Properties

The properties of a minimum spanning tree are:

• Possible multiplicity
  If there are n vertices in the graph, then each spanning tree has n − 1 edges.

• Uniqueness
  If each edge has a distinct weight then there will be only one, unique minimum spanning tree.

• Minimum-cost subgraph
  If the weights are positive, then a minimum spanning tree is in fact a minimum-cost subgraph connecting all vertices.

• Cycle property
  For any cycle C in the graph, if the weight of an edge e of C is larger than the individual weights of all other edges of C, then this edge cannot belong to a MST.

• Cut property
  For any cut C of the graph, if the weight of an edge e in the cut-set of C is strictly smaller than the weights of all other edges of the cut-set of C, then this edge belongs to all MSTs of the graph.

• Minimum-cost edge
  If the minimum cost edge e of a graph is unique, then this edge is included in any MST.

• Contraction
  If T is a tree of MST edges, then we can contract T into a single vertex while maintaining the invariant that the MST of the contracted graph plus T gives the MST for the graph before contraction.

Applications

The applications of Minimum Spanning Tree are:

• Minimum Spanning tree is used to describe/ design a network.
• Taxonomy.
• Cluster analysis: clustering points in the plane, single-linkage clustering (a method of hierarchical clustering), graph-theoretic clustering and clustering gene expression data.
• Constructing trees for broadcasting in computer networks. On Ethernet networks this is accomplished by means of the Spanning tree protocol.
• Image registration and segmentation (minimum spanning tree-based segmentation).
• Curvilinear feature extraction in computer vision.
• Handwriting recognition of mathematical expressions.
• Circuit design: implementing efficient multiple constant multiplications, as used in finite impulse response filters.
• Regionalisation of socio-geographic areas, the grouping of areas into homogeneous, contiguous regions.
• Comparing ecotoxicology data.
• Topological observability in power systems.
• Measuring homogeneity of two-dimensional materials.
• Minimax process control.
• Minimum spanning trees can also be used to describe financial markets.