
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
In this article, we will understand the complexity notations for Algorithms along with Big-O, Big-Omega, B-Theta and Little-O and see how we can calculate the complexity of any algorithm.
The notations we use to describe the asymptotic running time of an algorithm are defined in terms of functions whose domains are the set of natural numbers $\mathbb{N} = {0, 1, 2,...}.$ such notations are convenient to describing the worst-case running time function $T(n)$, which usually is defined only on integer input sizes. Computer scientists make heavy use of a specialized asymptotic notation to describe the growth of functions approximately.
We explore the following sub-topics:
- Big-O notation, Big-Omega and Big-Theta notation
- Little-O notation
- How to Calculate Complexity of any algorithm
Intuition
Asymptotic notation provides the basic vocabulary for discussing the design and analysis of algorithms. It's important that we as a algorithm lover, to know what programmers mean when they say that one piece of code run in "big-O of n time", while another runs in "big-O n squared time".
This vocabulary is so ubiquitous because it identifies the right spot for the reasoning about algorithms. Asymptotic notation is coarse enough to suppress all the details we want to ignore-details that depend on the choice of architecture, choice of programming language, the choice of compiler, and so on. On the other hand, it's precise enough to make useful comparisons between different high-level algorithmic approaches to solving a problem,especially on larger inputs(the input that require algorithmic ingenuity).
For example, asymptotic analysis helps us to differentiate between better and worse approaches to sorting, multiplying two integers , and so on.
High Level Idea:-
If we ask a practicing programmer to explain the point of asymptotic notation, he or she is likely to say something like the following:
The basic idea of Asympototic Notation is to supress constant factors and lower-order terms
constant factors - too system-dependent
lower-order terms - irrelevant for large inputs
Example: Equate $6nlog_2n + 6$ with just $nlogn$.
Terminology: Running time is $O(nlogn)$ $["big-Oh"\mbox{of } nlogn]$
where $n$ = input size(e.g. length of the input array)
Examples
- Searching One Array:
Input: array $A$ of integers, and an integer $t$.
Output: Whether or not $A$ contains $t$.
for i:= 1 to n do
if A[i] = t then
return TRUE
return FLASE
Since, We have not formally defined what big-O notation means yet, but
from our intuitive discussion so far you might be able to guess the
asymptotic running time of the code above.
Asymptotic running time - $O(n)$
- Searching Two Arrays:
Input: arrays $A$ and $B$ of n integers each, and an integer t.
Output: Whether or not $A$ or $B$ contains t.
for i:= 1 to n do
if A[i] = t then
return TRUE
for i:= 1 to n do
if B[i] = t then
return TRUE
return FALSE
Asymptotic running time - $O(n)$
- Checking For Duplicates:
Input: array of n integers.
Output: Whether or not $A$ contains an integer more than once.
for i := 1 to n do
for j := i + 1 to n do
if A[i] = A[j] then
return TRUE
return FALSE
Asymptotic running time - $O(n^2)$
2. Big-O Notation
Definition:
English definition:-
Big-O notation indicates maximum time required by an algorithm for all input values.
Let $T(n)$ = function on n = 1, 2, 3,... [usually, the worst-case running time of an algorithm]
$T(n) = O(f(n))$ if and only if $T(n)$ is eventually bounded above by a constant multiple of $f(n)$ (asymptotic upper bound).
Pictorial Definition:-:
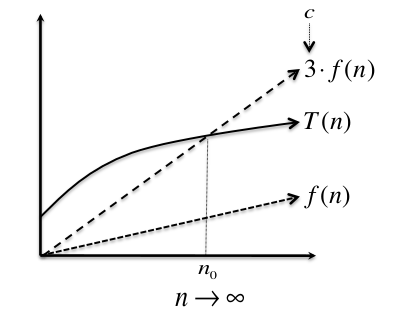
$T(n)$ is not bounded above by $f(n)$ , but by multiplying $f(n)$ by 3 results in the upper dashed line, which does lie above $T(n)$ once we go far enough to right on the graph, after the "crossover point" at $n_0$. since $f(n)$ is indeed eventually bounded above by a constant multiple of $f(n)$, we can say that $T(n) = O(f(n))$.
Mathematical Definition:-
$T(n) = O(f(n))$ if and only if $\exists$ positive constants $c, n_0$ such that
$$T(n) \leq c.f(n) \mbox{ [2.1]}$$
$$\forall n\geq n_0$$
Proof:-
A game-theoretic view.
If we want to prove that $T(n) = O(f(n))$, for example to prove that the asymptotic running time of an algorithm is linear in the input size(corresponding to $f(n) = n$), then our task is to choose the constants $c$ and $n_0$ so that $[2.1]$ holds whenever $n \geq n_0$.
One way to think about this is game-theoretically, as a contest between you and an opponent. You go first, and have to commit to constants $c$ and $n_0$ . Your opponent goes second and can choose any integer $n$ that is at least $n_0$ . You win if $[2.1]$ holds, your opponent wins if the opposite inequality $T(n) \geq c·f(n)$ holds.
If $T(n) = O(f(n))$, then there are constants $c$ and $n_0$ such that $[2.1]$ holds for all $n \geq n_0$ , and you have a winning strategy
in this game. Otherwise, no matter how you choose $c$ and $n_0$ , your
opponent can choose a large enough $n\geq n_0$ to flip the inequality and win the game.
Warning:- When we say that $c$ and $n_0$ are constants, we mean tey can't depend on n. For example, in figure $[2.1]$ $c$ and $n_0$ were fixed numbers(like 3 or 1000), and we then considered the inequality $[2.1]$ as n grows arbitrarily large(looking rightward on the graph toward infinity). If we never find ourself saying "take $n_0 = n$" or "take $c = \log_2n$" i an alleged big-O proof, we need to start over with the choices of $c$and $n_0$ that are independent on $n$.
Example:-
Claim: if $T(n) = a_kn^k + ... + a_1n + a_0$ then $T(n) = O(n^k)$
Proof: Choose $n_0 = 1$ and $c = |a_k| + |a_{k-1}| + ... + |a_1| + |a_0|$
Need to show that $\forall n \geq 1, T(n) \leq c.n^k$
We have, for every $n \geq 1$,
$$T(n) \leq |a_k|n^{k} + ... + |a1|n + |a_0|$$
$$\leq |a_k|n^{k} + ... + |a1|n^k + |a_0|n^k$$
$$ = c.n^k $$
So, according to theorem $[2.1]$ we can say that the claim is true.
3. Big-Omega and Big-Theta Notation
Big-O notation is by far the most important and ubiquitous concept for discussing the asymptotic running time of algorithms. A couple of its close relatives, the big-omega and big-theta notations, are also worth knowing. If big-O is analogous to “less than or equal to ($\leq$),” then big-omega and big-theta are analogous to “greater than or equal to ($\geq$),” and “equal to (=),” respectively. Let’s now treat them a little more precisely.
Big-Omega Notation:-
Definition:-
English Definition:-
$T(n)$ is big-omega of another function $f(n)$ if and only if $T(n)$ is eventually bounded below by a constant multiple of $f(n)$. In this case, we write $T(n) = \Omega(f(n))$. As before, we use two constants $c$ and $n_0$ to quantify “constant multiple” and “eventually.”
Pictorial Definition:-
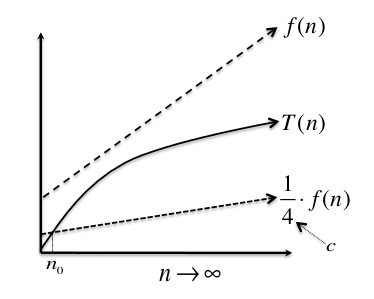
Function $f(n)$ does not bound $T(n)$ from below, but if we multiply it by the constant $c = 14$, the result (the lower dashed line) does bound $T(n)$ from below for all $n$ past the crossover point at $n_0$. Thus $T(n) = \Omega(f(n))$.
Mathematical Definition
$T(n) = \Omega(f(n))$ if and only if $\exists$ positive constants $c, n_0$ such that
$$T(n) \geq c.f(n) \mbox{ [3.1]}$$
$$\forall n\geq n_0$$
Big-Theta Notation:-
Big-theta notation, or simply theta notation, is analogous to “equal to.” Saying that $T(n) = \Theta(f(n))$ just means that both $T(n) = \Omega(f(n))$ and $T(n) = O(f(n))$. Equivalently, $T(n)$ is eventually sandwiched between two different constant multiples ($c_1, c_2$) of $f(n)$.
Mathematical Definition:-
$T(n) = \Theta(f(n))$ if and only if $\exists$ positive constants $c_1, c_2, n_0$ such that
$$c_1.f(n) \leq T(n) \leq c_2.f(n) \mbox{ [3.2]}$$
$$\forall n\geq n_0$$
4. Little-O notation
There is one final piece of asymptotic notation, “little-o notation,”
that you see from time to time. If big-O notation is analogous to
“less than or equal to,” little-o notation is analogous to “strictly less than".
Mathematical Definition:-
$T(n) = o(f(n))$ if and only if $\exists$ positive constants $c, n_0$ such that
$$T(n) \leq c.f(n) \mbox{ [4.1]}$$
$$\forall n\geq n_0$$
Where Does Notation Come From?
Asymptotic notation was not invented by computer scientists — it has been used in number theory since around the turn of the 20th century. Donald E. Knuth, the grandfather of the formal analysis of algorithms, proposed using it as the standard language for discussing rates of growth, and in particular for algorithm running times.
“On the basis of the issues discussed here, I propose that members of SIGACT, 8 and editors of computer science and mathematics journals, adopt the $O$, $\Omega$, and $Theta$ notations as defined above, unless a better alternative can be found reasonably soon.”
5. How to Calculate Complexity of any algorithm
Let's calculate asymptotic complexities of algorithms...
The algorithm flow might be two type's
- Iterative
- Recursive
1. Iterative:-
First of all let’s consider simple programs that contain no function calls. The rule of thumb to find an upper bound on the time complexity of such a program is:
- estimate the maximum number of times each loop can be executed,
- add these bounds for cycles following each other.
- multiply these bounds for nested cycles/parts of code,
Example 1. Estimating the time complexity of a random piece of code
int result = 0; // 1
for (int i = 0; i < N; i++) // 2
for (int j = i; j < N; j++){ // 3
for (int k = 0; k < M; k++){ // 4
int x = 0; // 5
while(x < N){ result++; x += 3; } // 6
} // 7
for (int k = 0; k < 2*M; k++) // 8
if (k%7 == 4) result++; // 9
} // 10
The time complexity of the while-cycle in line 6 is clearly $O(N)$ – it is executed no more than $\frac{N}{3} + 1$ times.
Now consider the for-cycle in lines 4-7. The variable $k$ is clearly incremented $O(M)$ times. Each time the whole while-cycle in line 6 is executed. Thus the total time complexity of the lines 4-7 can be bounded by $O(MN)$.
The time complexity of the for-cycle in lines 8-9 is $O(M)$. Thus the execution time of lines 4-9 is $O(MN + M) = O(MN)$.
This inner part is executed $O(N^2)$ times – once for each possible combination of $i$ and $j$. (Note that there are only $\frac{N(N + 1)}{2}$ possible values for $[i, j]$. Still, $O(N^2)$ is a correct upper bound.)
From the facts above follows that the total time complexity of the algorithm in Example 1 is $O(N^2.MN) = O(MN^3)$.
Let's take an another example.what will be running time complexity of following code?
for(int i = 1; i <= n; i++){
//...
}
For i = 1, number of operations = $2^{0}$, for i = 2, #operations = $2^{1}$, like-wise for i = n, #operations = $2^{k}$, so $2^{k} > n$, thus k = $log_{2}{n}$. So, Time Complexity will be $O(\log_{2}{n})$ <- Logarithm.
Hence we can compute running time complexity of any iterative algorithm.
Now, come to next part, How to compute time complexity of recursive algorithms.
1. Recursive:-
- We try to build recursive relation and try to extract running time complexity from that relation.
Let's Find recursive relation for given following program
fun(){
if(n > 1)
return f(n - 1) // base case
return n; // recursive case
}
By looking function we can evaluate and come-up with solution as below.
$$T(n) = { 1 + T(n-1), \mbox{ if } n > 1} \mbox{ //recursive case}$$
$$T(n) = {1 , \mbox{ if } n = 1} \mbox{ //base case}$$
Methods to solve recursive relations:-
a). Back Substitution Method
b). Recursion tree Method
a). Back Substitution Method:-
We expand the relation and calculate the variable value by using base cases and put them again in original relation to find time complexity.
Let's see how does it work?
$T(n) = 1 + T(n - 1)$, so
$T(n - 1) = 1 + T(n - 2)$
$....$
$T(n) = 1 + 1 + T(n - 2) => 1 + 1 + 1 + ... + T(n - k)$, where $k$ times 1's sum, So finally we get
$T(n) = k + T(n - k)$, Here by observation $k$ is number of recursive calls. It means $T(1) = 1$ (base case can be used) then $n - k = 1$ or $k = n - 1$. We got $T(n) = n - 1 + T(1) => T(n) = n$.
By using Big-Oh notation we can say, Time Complexity $T(n) = O(n)$.
b). Recursion tree Method:-
We try to build a recursion tree to get recursive relation and then come-up with a solution.
Steps:-
- Draw a recursion tree based on the given recurrence relation.
- Determine-
- Cost of each level
- Total number of levels in the recursion tree
- Number of nodes in the last level (#leaves)
- Cost of the last level
- Add cost of all the
levelsof the recursion tree and simplify the expression so obtained in terms of asymptotic notation.
Let's see a quick example
f(n){
if(n > 1){
for(int i = 0; i < n; i++) // n-operations
cout << "OpenGenus Foundation" << endl;
int l = f(n/2) + f(n/2); // recursive case
return l;
}
return 1; // base case
}
By looking at the problem we can see that
- A problem of size n will get divided into 2 sub-problems of size $\frac{n}{2}$.
- Then, each sub-problem of size $\frac{n}{2}$ will get divided into 2 sub-problems of size $\frac{n}{4}$ and so on.
- At the bottom most layer, the size of sub-problems will reduce to 1
This can be illustrated in the form of recursion tree
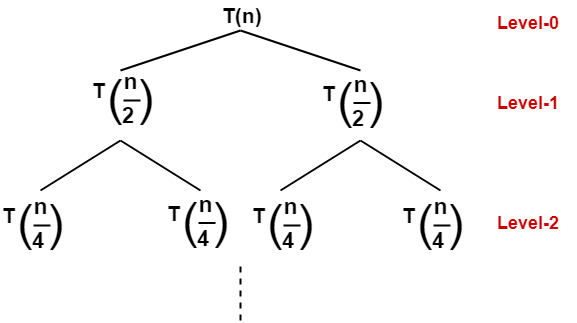
So, The recursive relation for this problem will be s follows
$$T(n) = 1, \mbox{ if n = 1} \mbox{ //base case}$$
$$T(n) = n + 2T(\frac{n}{2}), \mbox{ if n > 1} \mbox{//recursive case}$$
The given recurrence relation shows-
- The cost of dividing a problem of size $n$ into its 2 sub-problems and then combining its solution is n.
- The cost of dividing a problem of size $\frac{n}{2}$ into its 2 sub-problems and then combining its solution is $\frac{n}{2}$ and so on.
This is illustrated through following recursion tree where each node represents the cost of the corresponding sub-problem-
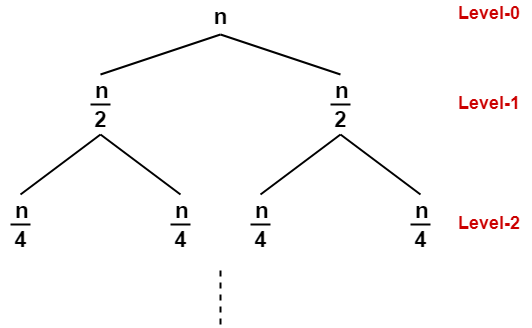
Now, Determine cost of each level-
- Cost of level-0 = $n$
- Cost of level-1 = $\frac{n}{2} + \frac{n}{2} = n$
- Cost of level-2 = $\frac{n}{4} + \frac{n}{4} + \frac{n}{4} + \frac{n}{4} = n$ and so on.
Now, Determine total number of levels in the recursion tree-
- Size of sub-problem at level-0 = $\frac{n}{2^{0}}$
- Size of sub-problem at level-1 = $\frac{n}{2^{1}}$
- Size of sub-problem at level-2 = $\frac{n}{2^{2}}$
In similar fashion, we have size of sub-problem at level-$i$ = $\frac{n}{2^{i}}$.
Suppose at level-$k$ (last level), size of sub-problem becomes 1. Then-
$$\frac{n}{2^{k}} = 1$$
$$2^{k} = n$$
Taking logarithm on both sides, we get-
$$k\log_{2}2 = \log_2(n)$$
$k = \log_{2}(n)$
$\therefore$Total number of levels in the recursion tree = $\log_{2}{n} + 1$
Now, Determine number of nodes in the last level-
- Level-0 has $2^{0}$ nodes i.e. 1 node
- Level-1 has $2^{1}$ nodes i.e. 2 nodes
- Level-2 has $2^{2}$ nodes i.e. 4 nodes
Continuing in similar manner, we have Level- $\log_{2}{n}$ has $2\log_{2}{n}$ nodes i.e. $n$ nodes
Determine cost of last level-
Cost of last level = $n\ast T(1) = \Theta(n)$
Add costs of all the levels of the recursion tree and simplify the expression so obtained in terms of asymptotic notation-
$$T(n) = {n + n + n + ... + n} + \Theta(n)$$
where sum of all $n$'s for $\log_{2}{n}$ levels/depth.
$=> n\ast log_{2}{n} + \Theta(n)$
$=> nlog_{2}{n} + \Theta(n)$
$=> \Theta(nlog_{2}{n})$
So, We can say that the asymptotic running time complexity for this problem is $T(n) = \Theta(nlog_{2}{n})$
By the same method we can calculate asymptotic time complexities of many algorithms like 'Quick-Sort', 'Merge-Sort' etc.
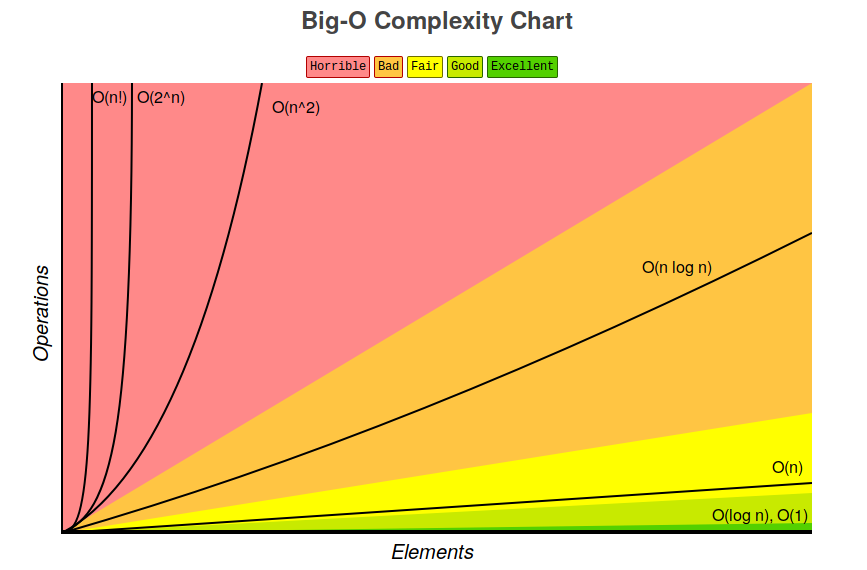
Computational Complexities comparison:
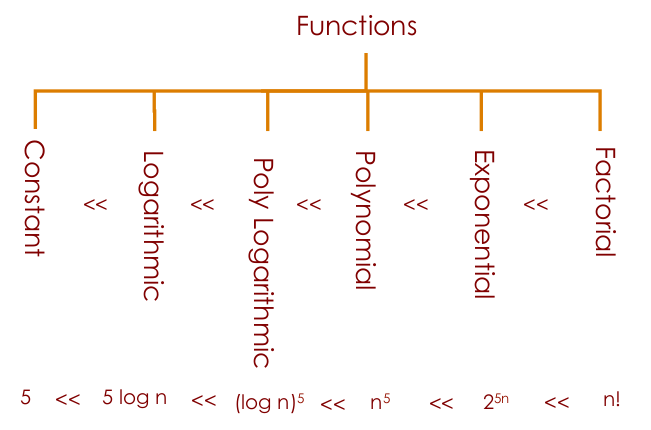
In the graphical view...
6. Summary
-
The purpose of asymptotic notation is to suppress constant factors (which are too system dependent) and lower-order terms (which are irrelevant for large inputs).
-
A function $T(n)$ is said to be “big-O of $f(n)$,” written “$T(n) = O(f(n))$,” if it is eventually(for sufficiently $n$) bounded above by a constant multiple of $f(n)$. That is, there are positive constants $c$ and $n_0$ such that $T(n) \leq c·f(n)$ for all $n \geq n_0$.
-
A function $T(n)$ is “big-omega of $f(n)$,” written “$T(n) = \Omega(f(n))$,” if it is eventually bounded below by a constant multiple of $f(n)$.
-
A function $T(n)$ is “big-theta of $f(n)$,” written “$T(n) = \Theta(f(n))$,” if both $T(n) = O(f(n))$ and $T(n) = \Omega(f(n))$.
-
A big-O statement is analogous to “less than or equal to,” big-omega to “greater than or equal to,” and big-theta to “equal to.”
7. Quiz
References:-
- Introduction to Algorithms, Thomas H.Cormen
- Stanford Algorithms specialization
- MIT OpenCourseWare
