In this article, we will learn what are set bits and how to count them. And we will also learn about Brian Kernighan's algorithm a famous algorithm to find the number of set bits in a number.

Table of content:

1. Introduction
2. Brute force method
3. Brian Kernighan's Algorithm
4. Complexity of Brian Kernighan's Algorithm
5. Conclusion

Introduction

Brian Kernighan's algorithm is used to calculate the number of set bits in a given number. But what is a set bit?

In computers, we know that data is represented as binary numbers 0s and 1s. Here 0 is called the unset bit and 1 is called the set bit. Thus, the number of set bits in a number means the number of 1's present in the binary number.

For example, let's take the number 34

The binary value of 34 is 100010

The total number of 1's present in 34 is 2. Hence the number of set bits in 34 is 2.

Well, we can count the number of set bits manually, but how to make the computer do this for us?

Here, we will discuss two ways to find the number of set bits in a number.

1. Using brute force
2. Brian Kernighan's algorithm.

Brute force method

In this method, we just loop through each bit of the number and check if it is a set bit i.e. 1.

Steps

1. we get the input number.
2. we initiate a variable to store the number of set bits.
3. we use a while loop that works on the condition the number is not equal to zero.
   • if n is not zero, we find the value of n & 1 and store it in the variable from step 2.
   • and then we shift the number n towards the right by 1.
4. This loop goes till the number becomes zero and then finally returns the number of set bits.

It looks like this when implemented in python.

def No_setbits(n):
    cnt = 0 # the counter variable
    while n != 0 :
        cnt += n & 1 # checks if the LSB is one 
        n = n >> 1 # remove the LSB

    return cnt # return the number of set bits

.

Let's break down to see what's happening in these lines of code. This function takes a number n as the input. And initializes a variable cnt as 0. Then the while loop starts operating if the number is not 0.

The next line performs a bitwise and operation on the least significant bit (the rightmost bit) with the number 1. And we know that the & operation returns 1 only if both of the bits are one. Thus, here if the LSB is 1 it returns 1 else it returns 0. As a result, the variable cnt gets increased by 1 every time the LSB is 1.

In the next line, the value of n is changed to n >> 1. It means the least significant bit (LSB) is deleted since we have already checked that bit in the previous line. Doing so in each iteration all the bits of the number will be deleted and finally, the number becomes zero and thus the loop ends.

And at last, we get what we wanted, the number of set bits in the given number.

Complexity

• The time complexity of the algorithms is O(log(n))
• The space complexity of the algorithm is O(1)

Brian Kernighan's Algorithm

The main idea behind this algorithm is that when we subtract one from any number, it inverts all the bits after the rightmost set bit i.e. it turns 1 to 0 and 0 to 1.

For example, see the binary representation of these numbers.

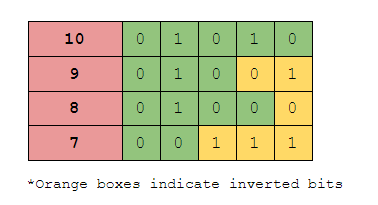
In the above image, we can see that how the bits are getting reversed each time we reduce the number by 1.

Note: The rightmost set bit also gets inverted along with the numbers right to it.

But how do we use this logic to find the number of set bits in a number? Let's understand it with the code.

Steps

1. Initialize a counter variable to count the number of set bits.
2. A while loop that works if the number is not equal to zero.
   • We increase the variable cnt by one.
   • And we update the number to the value of number & number -1.
3. The loop breaks when the number becomes zero.
4. As a result, we get the number of set bits as the output.

def Kenighan_algo(n):
    cnt = 0
    while n != 0 :
        cnt += 1
        n = n & n-1 # unsets the right most set bit.
           
    return cnt

.

This code is very similar to the brute force method, the only change in this method is the calculations that take place inside the while loop. Inside the while loop, the counter variable cnt is increased for each iteration, this is because of what happens in the next line. In the next line, the value of n is changed such that its rightmost set bit is reversed i.e. 1 is changed to 0.

So, if the rightmost set bits keep on getting reversed, the number eventually turns 0 and the loop ends.

For example, if n is 101010 then after the change n becomes 101000

Let's understand how this change happens, we know that when we subtract 1 from a number it inverts all the bits after the first set bit, and we also know that the bitwise and operation results in 1 only when both the inputs are 1.

Thus, when we perform bitwise and operation between n and n-1, all the bits after the rightmost set bit turns into zero.

I know it sounds a bit confusing, So let's see it with an example

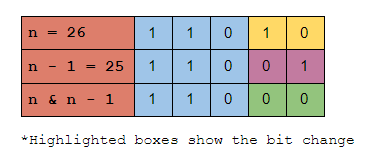
In the above image, we can see how the transformation takes place and how the rightmost set bit gets unset.

This is what happens in each iteration of the loop. Eventually, all the set bits i.e. the 1's in the number becomes 0, and the loop ends and returns the number of set bits as the output.

Complexity of Brian Kernighan's Algorithm

The time complexity of the algorithm is O(log(n)), where n is the number whose set bits need to be calculated. We can see that the time complexity of this algorithm is the same as the brute force method, it is because we are here seeing the worst-case scenario of the algorithm.

But when we see the best case or average case scenario the time complexity of this algorithm is way faster compared to the brute force method.

The space complexity of the algorithm is O(1).

Conclusion

With this article at OpenGenus, you must have the complete idea of Brian Kernighan's Algorithm.

This algorithm is just one of the basic applications of bitwise operations, there are a lot more applications to bitwise operators. So having good basics in them will always help you as a programmer.