Ever been amazed by plant's geometry? Lindenmayer systems,in short , L-systems have been inspired by the recurrence pattern observed in plants. We will learn more about L-systems , its history , applications and learn how L-systems were used to generate plants and trees models, snowflakes and so on. We later also make use of L-systems to attempt to generate carnatic music snippets based on raagas.

Introduction

L-system was developed in 1968 by Hungarian botanist named Aristid Lindenmayer to model plants mathematically.It is a type of grammar , where we form words using set of rules.L-system is based on rewriting and recursive functions. Basically we generate complex models by recursively generating and replacing with versions defined by set of rules.

L-systems consists of three components :
Alphabet , Axiom and Set of productions

• (V,w,p) : Where Alphabet(V) is the starting letter/instruction

• Axiom(w) means how Alphabet(V) can be changed.

• Set of productions are instructions of certain subsequences or subsets that can be transformed to another.

• L-systems - context free grammar , which means in case A->a , A can always be replaced by a and there no restrictions like context sensitive grammar.

Suppose we take an example where Alphabet - 'a' , Axiom - 'a'->'ab' and set of rules/ productions - 'b'-'a'
so,

  a
-> ab (a->ab)
-> aba (a-> ab and b->a)
-> abaab (a->ab , b->a and a->ab)
:
:

L-Systems are similar to Chomsky grammar but replacement in L-system takes place simultaneously.We can follow same rules and generate recursive patterns ,how? Rather than characters we will be printing directions.

Turtle representation

Turtle can be shown at a position (x,y,δ) where x,y are coordinates and alpha as angle , as per directions the turtle crawls thus leaving its impression.

• 'F' - go forward (on constant length).
• 'G' - go forward without leaving a trail.
• '+' - turn right on given rotation angle.
• '-' - turn left on given rotation angle.
• 'B' - go backwards

For 'F' we just move straight for certain specified length(s)
where new_x = x+s*cos(δ) and new_y = y+s*sin(δ)

For '+' we just turn δ angle if its positive then clockwise else anti clockwise and turn opposite for '-' for respective cases.'G' case will be just moving forward and no line will be made. Backward is opposite side of forward.

Edge rewriting

We have an initial starting polygon and then each of its edge is replaced by the initial structure.

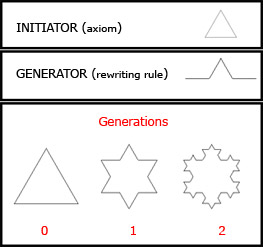
Here we can see that initially we have a polygon - triangle , whose edges are replaced by the rules and resultant figure's edges are again replaced by the rules to produce a snowflake .

Node rewriting

"The idea of node rewriting is to substitute new polygons for nodes of the predecessor curve."Here each polygon is substituted with nodes of previous curve .

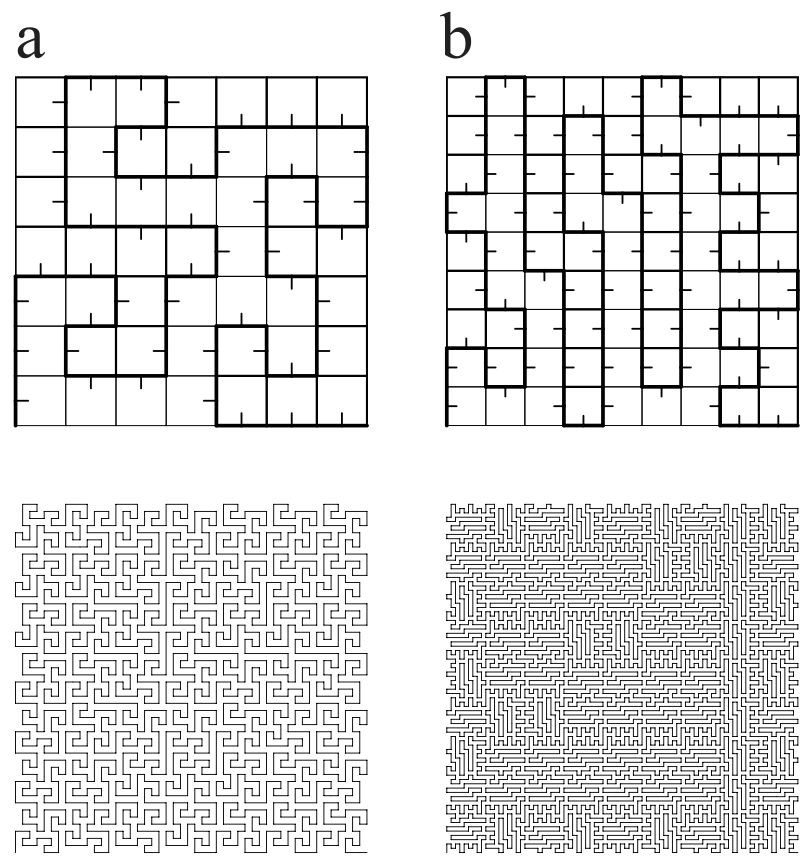
L-systems have been used to model plants and observe the patterns in plants , also used to draw fractals,snowflakes.

Snowflakes

import turtle
def lsystem(i,axiom):
    s = axiom
    e = ""
    for i1 in range(i):
        e = processe(s)
        s = e

    return e

def processe(old):
    news = ""
    for c in old:
        news = news + applyRules(c)

    return newstr

def apply(ch):
    news = ""
    if ch == 'F':
        news = 'F-F++F-F'   # Rule 1
    else:
        news = ch    # no rules apply so keep the character

    return newstr

def drawls(tturtle, instruction, angle, dist):
    for c in instruction:
        if c == 'F':
            tturtle.forward(dist)
        elif c == 'B':
            tturtle.backward(distance)
        elif c == '+':
            tturtle.right(angle)
        elif c == '-':
            tturtle.left(angle)
 def main():
    inst = lsystem(4, "F++F++F++F")   # create the string
    print(inst)
    t = turtle.Turtle()            # create the turtle
    wn = turtle.Screen()

    t.up()
    t.back(200)
    t.down()
    t.speed(9)
    drawls(t, inst, 60, 4)   # draw the picture
                                  # angle 120, segment length 4
    wn.exitonclick()
main()

Output :

Plants modelling

Bracketed L-systems

Now we introduce two new symbols -'[' and ']' for modelling plants where

• '[' signifies starting of the branch.
• ']' signifies ending of the branch.
• Just like stack problem of parenthesis.
• A stack can be used to append the positions at starting of the bracket and ended after the bracket ended.

#inside the lsystem function
stack=[]
    tturtle.left(angle)
        elif command == "[":
            stack.append((tturtle.position(), tturtle.heading()))
        elif command == "]":
            tturtle.pu()  # pen up - not drawing
            position, heading = stack.pop()
            tturtle.goto(position)
            tturtle.setheading(heading)

An axial tree with X->F-[[X]+X]+F[+FX]-X and F->FF axiom=X iterations=5 , angle(i)=22.5
X denotes X rule to be followed , wherever X is there , replace with X rule.

Carnatic Music generation using L-systems?

Can we try to generate music L-systems? We have now seen how using recursive techniques , L-system shows that plants can be modelled by replacing each node with structure similar to the total previous structure.Music also has elements of patterns associated with it .Carnatic music is a type of Indian Classical Music where we have songs composed by millions of arrangements of just 7 pitches!

Let us see an example of Abhogi Raagam -Varnam(a type of composition) named- "Evvari Bodhana"

• Raagam : Descending and ascending order of Arrangement of pitches of Carnatic music S R G M P D N analogous to Do Re Mi Fa So La Ti.
• Varnam : A type of Carnatic Music Composition.For simplicity let us call it a song.
• Abhogi Raagam : incr - S R G1 M D S decre - S D M G1 R S D
• Arohana means increasing order of pitches , Avarohana means decreasing order of pitches

G1 here denotes the lower G,and here D-D2 which means higher pitch D.
Let us see an excerpt of the song's pitches -
(Here ',' denotes a pause .)

R , G , G R S , S R S S D M D , |
M D S D , S- D S R G ,- M G G R S ||

If you observe , all the pitches are in line with the Abhogi Raagam.

Let us divide it into parts such that all parts are the substrings of either increasing or descending order of the raagam ,considered as the main string.
R,G, ---1
G R S ,---2
S R ---3
S --4
S D M ---5
D , ---6
M D S ---7
D , ---8
S D ---9
S R G ,---10
M G---11
G R S---12

We have seen that, the music is being generated keeping in mind the source of pitches are according to the rules of raagam. The raagam'subtrings are either being inverted or combined with others to generate musical composition.If we represent graphically , the structure of graph seems that it can be mimicked usign L-systems. But here we can see that , the raagam's substrings have been placed and its not necessary that all the pitches are used at once. Suppose if we want to use the same formula to generate music that was used to generate axial tree then where F signifies set of pitches/pitch then , what is F going to denote as F need not be complete raagam set as it can be any of the substring ?

Without L-systems probably we could pick out random substrings from the raagam string and compose a musical piece , but will L-system be of any use in here?

Here we try to slowly replicate the logic of L-system to produce carnatic music on lines of raagam , here we experiment on Mohana raagam whose swaras go like : s r2 g2 p d2 s

We make r2,g2,d2 as notes through which sub parts of raaga emanate as s and p are natural notes(prakruthi swaras) and are not allowed to have variations.

import numpy as np 
import pandas as pd
import random as rd
# 3 pitches
    octave = ['s','r1','r2','g1','g2','m1','m2','p','d1','d2','n1','n2'] 
    high = ['S','R1','R2','G1','G2','M1','M2','P','D1','D2','N1','N2'] 
    freq=[1,	16/15,	9/8,	6/5	,5/4,	4/3	,45/32,	3/2,	8/5,	5/3,	16/9,	15/8]
    base_freq = 261.63 #
    
    freqs = {octave[i]: base_freq * freq[i] for i in range(len(octave))} 
    hfreqs = {high[i]:2* base_freq * freq[i] for i in range(len(octave))}
    freqs.update(hfreqs)      
    freqs[''] = 0.0
    print(type(freqs))
from scipy.io.wavfile import write
import numpy as np

samplerate = 44100

def get_notes():
    '''
    Returns a dict object for all the piano 
    note's frequencies
    '''
    
    octave = ['s','r1','r2','g1','g2','m1','m2','p','d1','d2','n1','n2'] 
    high = ['S','R1','R2','G1','G2','M1','M2','P','D1','D2','N1','N2'] 
    low=['sa','ri1','ri2','ga1','ga2','ma1','ma2','pa','da1','da2','ni1','ni2']
    freq=[1,	16/15,	9/8,	6/5	,5/4,	4/3	,45/32,	3/2,	8/5,	5/3,	16/9,	15/8]
    base_freq = 261.63
    
    note_freqs = {octave[i]: base_freq * freq[i] for i in range(len(octave))} 
    hfreqs = {high[i]:2* base_freq * freq[i] for i in range(len(octave))}
    lfreqs = {low[i]:(1/2)* base_freq * freq[i] for i in range(len(octave))}
    note_freqs.update(hfreqs)  
    note_freqs.update(lfreqs)         
    note_freqs[''] = 0.0
    
    return note_freqs
    
def get_wave(freq, duration=0.5):
    amplitude = 262
    t = np.linspace(0, duration, int(samplerate * duration))
    wave = amplitude * np.sin(2 * np.pi * freq * t)
    
    return wave
    
def l_systems(note):
  if note=='r2':
    choices = ['r2','r2-s','r2-g2','r2-g2-p','r2-g2-p-d2','r2-g2-p-d2-S']
    ind = rd.choice(choices)
    return ind
  if note=='g2':
    choices = ['g2','g2-r2-s','g2-p','g2-p-d2','g2-p-d2-S']
    ind = rd.choice(choices)
    return ind 
  if note=='d2':
    choices = ['d2','d2-S','d2-p','d2-p-g2','d2-p-g2-r2','d2-p-g2-r2-s']
    ind = rd.choice(choices)
    return ind   

  return note

def get_song_data(music_notes):
    note_freqs = get_notes()
    notes=""
    for note in music_notes.split('-'):
      if(notes!=""):
        notes=notes+"-"+l_systems(note)
      else:
        notes=l_systems(note)
      print(notes)

    #for i in range(0,len(music_notes)-1):
      #notes=notes+(l_systems(music_notes[i]+music_notes[i+1]))
    #print(notes)
    song = [get_wave(note_freqs[note]) for note in notes.split('-')]
    song = np.concatenate(song)
    return song.astype(np.int16)


def main():
    
    music_notes = 's-r2-g2-p-d2-S-r2-g2-S-r2-p-g2'
    data = get_song_data(music_notes)
    data = data * (16300/np.max(data))
    write('song.wav', samplerate, data.astype(np.int16))
    
    
if __name__=='__main__':
    main()

Generated musical snippet

We used basic modification to change 's-r2-g2-p-d2-S-r2-g2-S-r2-p-g2' to this: 's-r2-g2-r2-s-p-d2-p-g2-S-r2-g2-p-g2-r2-s-S-r2-s-p-g2-p-d2'.

Now we iterate for 5 times where each time the generated snippet goes more changes and different orientation notes emerge.

def get_song_data(music_notes,iteration):
    note_freqs = get_notes()
    notes=""
    # iterate for 5 times
    # each iteration , updated string gets even more updated .
    for i in range(0,iteration):
      for note in music_notes.split('-'):
        if(notes!=""):
          notes=notes+"-"+l_systems(note)
        else:
          notes=l_systems(note)
        print(notes)
    song = [get_wave(note_freqs[note]) for note in notes.split('-')]
    song = np.concatenate(song)
    return song.astype(np.int16)

def main():
    
    music_notes = 's-r2-g2-p-d2-S-r2-g2-S-r2-p-g2'
    data = get_song_data(music_notes,5)
    data = data * (16300/np.max(data))
    write('song.wav', samplerate, data.astype(np.int16))

Generated snippet : link
Now we automate it even further . We generate substrings on our own for given raagam and then generate for the following swaras with variations - r,g,d,n

def substrings(pos,aro):
    res=[]
    res1=[]
    stri=''
    #generate substrings : eg 'r2','r2-s'..
    #based on arohana and avarohana(ascending and descending order of swaras)
    for i in range(pos,len(aro)):
      if(aro[i]=='2' or aro[i]=='1'):
        strin=aro[pos:i+1]
        res.append(strin)
      else:
        if(aro[i]=='S' or aro[i]=='s' or aro[i]=='p'):
          stri=stri+aro[i]
          strin = aro[pos:i+1]
          res.append(strin)
        
    return res

# We generate randomised systematic substrings for all vikruthi swaras
def l_systems(note,aro,ava):
  if note=='r2' or note=='r1':
    #choices = ['r2','r2-s','r2-g2','r2-g2-p','r2-g2-p-d2','r2-g2-p-d2-S']
    pos = aro.find(note)
    pos1=ava.find(note)
    
    res=substrings(pos,aro)
    res1=substrings(pos1,ava)
    res1=res1[1:]
    res=res1+res
    res.append('')
    res=np.asarray(res)
    #print(res)
    #choices=res
    ind = rd.choice(res)
    return ind
  if note=='g2' or note=='g1':
    pos = aro.find(note)
    pos1=ava.find(note)
    
    res=substrings(pos,aro)
    res1=substrings(pos1,ava)
    res1=res1[1:]
    res=res1+res
    res.append('')
    res=np.asarray(res)
    #print(res)
    #choices=res
    ind = rd.choice(res)
    return ind
  if note=='d2' or note=='d1':
    pos = aro.find(note)
    pos1=ava.find(note)
    
    res=substrings(pos,aro)
    res1=substrings(pos1,ava)
    res1=res1[1:]
    res=res1+res
    res.append('')
    res=np.asarray(res)
    #print(res)
    #choices=res
    ind = rd.choice(res)
    return ind   
  if note=='n2' or note=='n1':
    pos = aro.find(note)
    pos1=ava.find(note)
    
    res=substrings(pos,aro)
    res1=substrings(pos1,ava)
    res1=res1[1:]
    res=res1+res
    res.append('')
    res=np.asarray(res)
    #print(res)
    #choices=res
    ind = rd.choice(res)
    return ind 

  return note

def get_song_data(music_notes,iteration,ragam):
    note_freqs = get_notes()
    aro = ragam[0]
    ava = ragam[1]

    notes=""
    for i in range(0,iteration):
      for note in music_notes.split('-'):
        if(notes!=""):
          notes=notes+"-"+l_systems(note,aro,ava)
        else:
          notes=l_systems(note,aro,ava)
        print(notes)
    song = [get_wave(note_freqs[note])[0] for note in notes.split('-')]
    t=[get_wave(note_freqs[note])[1] for note in notes.split('-')]
    song = np.concatenate(song)
    t=np.concatenate(t)
    return song.astype(np.int16),t

This time we experiment with Abhogi raagam : Abhogi snippet

Conclusion

With this article at OpenGenus, you must have a strong foundation on L System.

As the knowledge regarding carnatic music evolves , more variations can be accomodated in the code.Hence L-systems are simple algorithms used for change and regeneration and using L-systems we have tried to produce carnatic music given the raagam and their arohana and avarohana.We can further improve the algorithm by tuning the sound so that it appears more realistic or like some Indian Instruments.We can also improve the algorithm in such a manner that it produces systematic compostions(Varnam,Krithi,Kirthi etc)

This is the colab link to musical lsystems