
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 25 minutes | Coding time: 12 minutes
In this article, we have explored the divide and conquer approach towards finding the convex hull of a set of points. The key idea is that is we have two convex hull then, they can be merged in linear time to get a convex hull of a larger set of points.
Divide and conquer algorithms solve problems by dividing them into smaller instances, solving each instance recursively and merging the corresponding results to a complete solution. Further, asserts that all instances have exactly the same structure as the original problem and can be solved independently from each other, and so can easily be distributed over a number of parallel processes or threads. These algorithms exploit the fact that solutions to smaller problems can be used to solve larger problems.
Algorithm
Given S: the set of points for which we have to find the convex hull.
Let us divide S into two sets:
- S1: the set of left points
- S2: the set of right points
Note that all points in S1 is left to all points in S2.
Suppose we know the convex hull of the left half points S1 is C1 and the right half points S2 is C2.
Then the problem now is to merge these two convex hulls C1 and C2 and determine the convex hull C for the complete set S.
This can be done by finding the upper and lower tangent to the right and left convex hulls C1 and C2.
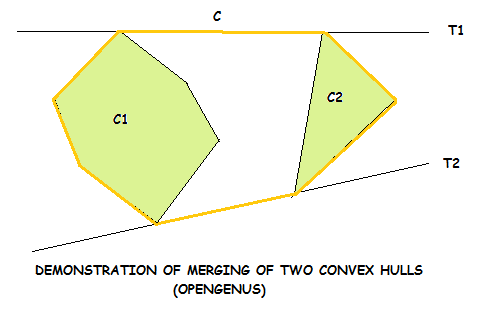
Let the left convex hull be C1 and the right convex hull be C2. Then the lower and upper tangents are named as T1 and T2 respectively, as shown in the figure.
Then the red outline shows the final convex hull.
How to find the convex hull for the left and right half S1 and S2?
Now recursion comes into the picture, we divide the set of points until the number of points in the set is very small, say 5, and we can find the convex hull for these points by the brute force algorithm. The merging of these halves would result in the convex hull for the complete set of points.
Tangents between two convex polygons
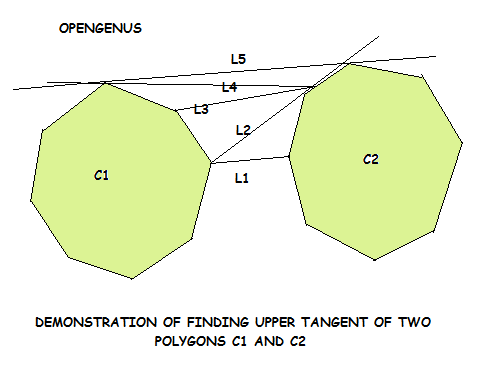
For finding the upper tangent, we start by taking two points.
The rightmost point (say A) of left convex hull C1 and leftmost point (say B) of right convex hull C2. The line joining them is labelled as L1.
As this line passes through the polygon C2 (is not above polygon b) so we take the anti-clockwise next point on C2, the line is labelled 2. Now the line is above the polygon C2, fine! But the line is crossing the polygon C1, so we move to the clockwise next point, labelled as 3 in the picture. This again crossing the polygon a so we move to line 4. This line is crossing b so we move to line 5. Now this line is crossing neither of the points. So this is the upper tangent for the given polygons.
For finding the lower tangent we need to move inversely through the polygons i.e. if the line is crossing the polygon C2 we move to clockwise next and to anti-clockwise next if the line is crossing the polygon C1.
Pseuodocode
Pseudocode for finding upper tangent and lower tangent is as follows:
For Upper Tangent
L <- line joining the rightmost point of a
and leftmost point of b.
while (L crosses any of the polygons)
{
while(L crosses b)
L <- L' : the point on b moves up.
while(L crosses a)
L <- L' : the point on a moves up.
}
For Lower Tangent
L <- line joining the rightmost point of a
and leftmost point of b.
while (L crosses any of the polygons)
{
while (L crosses b)
L <- L' : the point on b moves down.
while (L crosses a)
L <- L' : the point on a moves down.
}
Implementations
The implementation of the divide and Conquer approach towards finding Convex Hull in C++ is as follows:
- C++
C++
// A divide and conquer program to find convex
// hull of a given set of points.
#include<bits/stdc++.h>
using namespace std;
// stores the centre of polygon (It is made
// global because it is used in compare function)
pair<int, int> mid;
// determines the quadrant of a point
// (used in compare())
int quad(pair<int, int> p)
{
if (p.first >= 0 && p.second >= 0)
return 1;
if (p.first <= 0 && p.second >= 0)
return 2;
if (p.first <= 0 && p.second <= 0)
return 3;
return 4;
}
// Checks whether the line is crossing the polygon
int orientation(pair<int, int> a, pair<int, int> b,
pair<int, int> c)
{
int res = (b.second-a.second)*(c.first-b.first) -
(c.second-b.second)*(b.first-a.first);
if (res == 0)
return 0;
if (res > 0)
return 1;
return -1;
}
// compare function for sorting
bool compare(pair<int, int> p1, pair<int, int> q1)
{
pair<int, int> p = make_pair(p1.first - mid.first,
p1.second - mid.second);
pair<int, int> q = make_pair(q1.first - mid.first,
q1.second - mid.second);
int one = quad(p);
int two = quad(q);
if (one != two)
return (one < two);
return (p.second*q.first < q.second*p.first);
}
// Finds upper tangent of two polygons 'a' and 'b'
// represented as two vectors.
vector<pair<int, int>> merger(vector<pair<int, int> > a,
vector<pair<int, int> > b)
{
// n1 -> number of points in polygon a
// n2 -> number of points in polygon b
int n1 = a.size(), n2 = b.size();
int ia = 0, ib = 0;
for (int i=1; i<n1; i++)
if (a[i].first > a[ia].first)
ia = i;
// ib -> leftmost point of b
for (int i=1; i<n2; i++)
if (b[i].first < b[ib].first)
ib=i;
// finding the upper tangent
int inda = ia, indb = ib;
bool done = 0;
while (!done)
{
done = 1;
while (orientation(b[indb], a[inda], a[(inda+1)%n1]) >=0)
inda = (inda + 1) % n1;
while (orientation(a[inda], b[indb], b[(n2+indb-1)%n2]) <=0)
{
indb = (n2+indb-1)%n2;
done = 0;
}
}
int uppera = inda, upperb = indb;
inda = ia, indb=ib;
done = 0;
int g = 0;
while (!done)//finding the lower tangent
{
done = 1;
while (orientation(a[inda], b[indb], b[(indb+1)%n2])>=0)
indb=(indb+1)%n2;
while (orientation(b[indb], a[inda], a[(n1+inda-1)%n1])<=0)
{
inda=(n1+inda-1)%n1;
done=0;
}
}
int lowera = inda, lowerb = indb;
vector<pair<int, int>> ret;
//ret contains the convex hull after merging the two convex hulls
//with the points sorted in anti-clockwise order
int ind = uppera;
ret.push_back(a[uppera]);
while (ind != lowera)
{
ind = (ind+1)%n1;
ret.push_back(a[ind]);
}
ind = lowerb;
ret.push_back(b[lowerb]);
while (ind != upperb)
{
ind = (ind+1)%n2;
ret.push_back(b[ind]);
}
return ret;
}
// Brute force algorithm to find convex hull for a set
// of less than 6 points
vector<pair<int, int>> bruteHull(vector<pair<int, int>> a)
{
// Take any pair of points from the set and check
// whether it is the edge of the convex hull or not.
// if all the remaining points are on the same side
// of the line then the line is the edge of convex
// hull otherwise not
set<pair<int, int> >s;
for (int i=0; i<a.size(); i++)
{
for (int j=i+1; j<a.size(); j++)
{
int x1 = a[i].first, x2 = a[j].first;
int y1 = a[i].second, y2 = a[j].second;
int a1 = y1-y2;
int b1 = x2-x1;
int c1 = x1*y2-y1*x2;
int pos = 0, neg = 0;
for (int k=0; k<a.size(); k++)
{
if (a1*a[k].first+b1*a[k].second+c1 <= 0)
neg++;
if (a1*a[k].first+b1*a[k].second+c1 >= 0)
pos++;
}
if (pos == a.size() || neg == a.size())
{
s.insert(a[i]);
s.insert(a[j]);
}
}
}
vector<pair<int, int>>ret;
for (auto e:s)
ret.push_back(e);
// Sorting the points in the anti-clockwise order
mid = {0, 0};
int n = ret.size();
for (int i=0; i<n; i++)
{
mid.first += ret[i].first;
mid.second += ret[i].second;
ret[i].first *= n;
ret[i].second *= n;
}
sort(ret.begin(), ret.end(), compare);
for (int i=0; i<n; i++)
ret[i] = make_pair(ret[i].first/n, ret[i].second/n);
return ret;
}
// Returns the convex hull for the given set of points
vector<pair<int, int>> divide(vector<pair<int, int>> a)
{
// If the number of points is less than 6 then the
// function uses the brute algorithm to find the
// convex hull
if (a.size() <= 5)
return bruteHull(a);
// left contains the left half points
// right contains the right half points
vector<pair<int, int>>left, right;
for (int i=0; i<a.size()/2; i++)
left.push_back(a[i]);
for (int i=a.size()/2; i<a.size(); i++)
right.push_back(a[i]);
// convex hull for the left and right sets
vector<pair<int, int>>left_hull = divide(left);
vector<pair<int, int>>right_hull = divide(right);
// merging the convex hulls
return merger(left_hull, right_hull);
}
// Driver code
int main()
{
vector<pair<int, int> > a;
a.push_back(make_pair(0, 0));
a.push_back(make_pair(1, -4));
a.push_back(make_pair(-1, -5));
a.push_back(make_pair(-5, -3));
a.push_back(make_pair(-3, -1));
a.push_back(make_pair(-1, -3));
a.push_back(make_pair(-2, -2));
a.push_back(make_pair(-1, -1));
a.push_back(make_pair(-2, -1));
a.push_back(make_pair(-1, 1));
int n = a.size();
// sorting the set of points according
// to the x-coordinate
sort(a.begin(), a.end());
vector<pair<int, int> >ans = divide(a);
cout << "convex hull:\n";
for (auto e:ans)
cout << e.first << " "
<< e.second << endl;
return 0;
}
Complexity
The merging of the left and the right convex hulls take O(n) time and as we are dividing the points into two equal parts, so the time complexity of the above algorithm is O(n * log n).
- Worst case time complexity:
Θ(N log N) - Average case time complexity:
Θ(N log N) - Best case time complexity:
Θ(N log N) - Space complexity:
Θ(N)
Advantages
The advantages of using the Divide and Conquer approach towards Convex Hull is as follows:
Divide-and-conquer algorithms are adapted for execution in multi-processor machines, especially shared memory systems as in the testing of robots using convex hulls where the communication of data between processors does not need to be planned in advance. Thus distinct sub-problems can be executed on different processors.
Ideal for solving difficult and complex problems
Divide and conquer is a powerful tool for solving conceptually difficult problems, such as the classic Tower of Hanoi puzzle: all it requires is a way of breaking the problem into sub-problems,of solving the trivial cases and of combining sub-problems to the original problem.
Memory access
Divide-and-conquer algorithms naturally tend to make efficient use of memory caches. The reason is that once a sub-problem is small enough, it and all its sub-problems can, in principle, be solved within the cache, without accessing the slower main memory. An algorithm designed to exploit the cache in this way is called cache oblivious because it does not contain the cache size(s) as an explicit parameter.
Disadvantages
The disadvantages of using the Divide and Conquer approach towards Convex Hull is as follows:
- Recursion which is the basis of divide and conquer is slow, the overhead of the repeated subroutine calls, along with that of storing the call stack.
- Inability to control or guarantee sub-problem size results in sub-optimum worst case time performance.
- Requires a lot of memory for storing intermediate results of sub-convex hulls to be combined to form the complete convex hull.
- The use of divide and conquer is not ideal if the points to be considered are too close to each other such that other approaches to convex hull will be ideal.
Applications
The applications of this Divide and Conquer approach towards Convex Hull is as follows:
- Collision avoidance: If the convex hull of a car avoids collision with obstacles then so does the car. Since the computation of paths that avoid collision is much easier with a convex car, then it is often used to plan paths.

-
Smallest box: The smallest area rectangle that encloses a polygon has at least one side flush with the convex hull of the polygon, and so the hull is computed at the first step of minimum rectangle algorithms. Similarly, finding the smallest three-dimensional box surrounding an object depends on the 3D-convex hull.
-
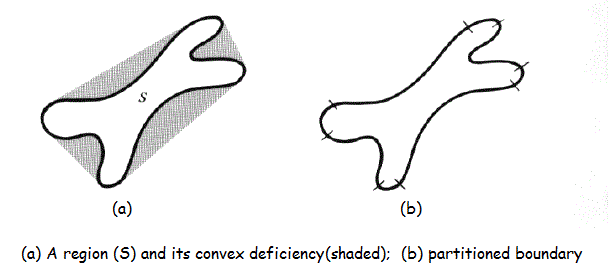
Shape analysis: Shapes may be classified for the purposes of matching by their "convex deficiency trees", structures that depend for their computation on convex hulls.
-
Other practical applications are pattern recognition, image processing, statistics, geographic information system, game theory, construction of phase diagrams, and static code analysis by abstract interpretation.
-
It also serves as a tool, a building block for a of other computational-geometric algorithms such as the rotating calipers method for computing the width and diameter of a point set.
