
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 20 minutes | Coding time: 10 minutes
Activity Selection problem is a approach of selecting non-conflicting tasks based on start and end time and can be solved in O(N logN) time using a simple greedy approach. Modifications of this problem are complex and interesting which we will explore as well. Suprising, if we use a Dynamic Programming approach, the time complexity will be O(N^3) that is lower performance.
The problem statement for Activity Selection is that "Given a set of n activities with their start and finish times, we need to select maximum number of non-conflicting activities that can be performed by a single person, given that the person can handle only one activity at a time." The Activity Selection problem follows Greedy approach i.e. at every step, we can make a choice that looks best at the moment to get the optimal solution of the complete problem.
Our objective is to complete maximum number of activities. So, choosing the activity which is going to finish first will leave us maximum time to adjust the later activities. This is the intuition that greedily choosing the activity with earliest finish time will give us an optimal solution. By induction on the number of choices made, making the greedy choice at every step produces an optimal solution, so we chose the activity which finishes first. If we sort elements based on their starting time, the activity with least starting time could take the maximum duration for completion, therefore we won't be able to maximise number of activities.
Algorithm
The algorithm of Activity Selection is as follows:
Activity-Selection(Activity, start, finish)
Sort Activity by finish times stored in finish
Selected = {Activity[1]}
n = Activity.length
j = 1
for i = 2 to n:
if start[i] ≥ finish[j]:
Selected = Selected U {Activity[i]}
j = i
return Selected
Complexity
Time Complexity:
When activities are sorted by their finish time: O(N)
When activities are not sorted by their finish time, the time complexity is O(N log N) due to complexity of sorting
Example
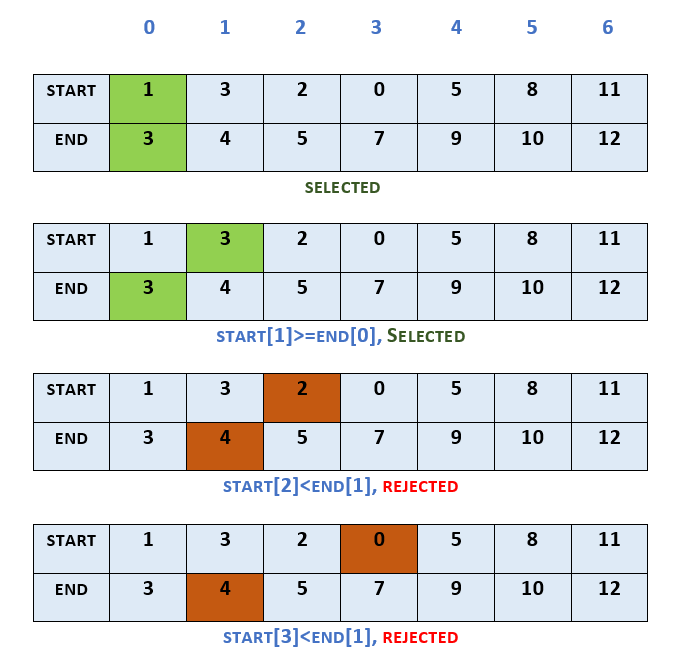
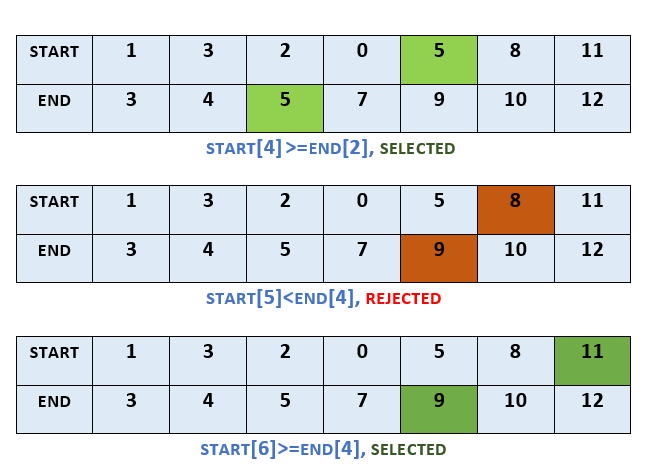
In this example, we take the start and finish time of activities as follows:
start = [1, 3, 2, 0, 5, 8, 11]
finish = [3, 4, 5, 7, 9, 10, 12]
Sorted by their finish time, the activity 0 gets selected. As the activity 1 has starting time which is equal to the finish time of activity 0, it gets selected. Activities 2 and 3 have smaller starting time than finish time of activity 1, so they get rejected. Based on similar comparisons, activities 4 and 6 also get selected, whereas activity 5 gets rejected. In this example, in all the activities 0, 1, 4 and 6 get selected, while others get rejected.
Question
Which approach is more efficient for Activity Selection Problem?
Implementations
Implementation of Activity Selection problem in 5 languages that includes C, C++, Java, Python and Go.
- C
- C++
- Java
- Python
- Go
C++
// C Code for Activity Selection
#include <stdio.h>
// Function for Activity Selection
void ActivitySelection(int start[], int finish[], int n)
{
printf("The following activities are selected:\n");
int j = 0;
printf("%d ", j);
int i;
for (i = 1; i < n; i++)
{
if (start[i] >= finish[j])
{
printf("%d ", i);
j = i;
}
}
}
// Driver function
int main()
{
int start[] = {1, 3, 2, 0, 5, 8, 11};
int finish[] = {3, 4, 5, 7, 9, 10, 12};
int n = sizeof(start) / sizeof(start[0]);
ActivitySelection(start, finish, n);
return 0;
}
/* Output
The following activities are selected:
0 1 4 6
*/
// C++ Code for Activity Selection
#include <bits/stdc++.h>
using namespace std;
// Function for Activity Selection
void ActivitySelection(int start[], int finish[], int n)
{
cout<<"The following activities are selected:"<<endl;
int j = 0;
cout<<j<<" ";
for (int i = 1; i < n; i++)
{
if (start[i] >= finish[j])
{
cout<<i<<" ";
j = i;
}
}
}
// Driver function
int main()
{
int start[] = {1, 3, 2, 0, 5, 8, 11};
int finish[] = {3, 4, 5, 7, 9, 10, 12};
int n = sizeof(start) / sizeof(start[0]);
ActivitySelection(start, finish, n);
return 0;
}
/* Output
The following activities are selected:
0 1 4 6
*/
Java
// Java Code for Activity Selection
class activityselection
{
// Function for Activity Selection
public static void ActivitySelection(int start[], int finish[], int n)
{
System.out.println("The following activities are selected:");
int j = 0;
System.out.print(j+" ");
for (int i = 1; i < n; i++)
{
if (start[i] >= finish[j])
{
System.out.print(i+" ");
j = i;
}
}
}
// Driver function
public static void main(String args[])
{
int start[] = {1, 3, 2, 0, 5, 8, 11};
int finish[] = {3, 4, 5, 7, 9, 10, 12};
int n = start.length;
activityselection obj= new activityselection();
obj.ActivitySelection(start, finish, n);
}
}
/* Output
The following activities are selected:
0 1 4 6
*/
Python
# Python Code for Activity Selection
# Function for Activity Selection
def ActivitySelection(start, finish, n):
print("The following activities are selected:");
j = 0
print(j,end=" ")
for i in range(1,n):
if start[i] >= finish[j]:
print(i,end=" ")
j = i
# Driver Code
start = [1, 3, 2, 0, 5, 8, 11]
finish = [3, 4, 5, 7, 9, 10, 12]
n = len(start)
ActivitySelection(start, finish, n)
# Output
# The following activities are selected:
# 0 1 4 6
Go
// Go Code for Activity Selection
package main
import "fmt"
// Function for Activity Selection
func ActivitySelection(start[] int, finish[] int, n int) {
fmt.Println("The following activities are selected:")
j:= 0
fmt.Printf("%d ",j)
for i := 1; i < n; i++ {
if start[i] >= finish[j] {
fmt.Printf("%d ",i)
j = i;
}
}
}
// Driver function
func main() {
start := []int{1, 3, 2, 0, 5, 8, 11}
finish := []int{3, 4, 5, 7, 9, 10, 12}
n := len(start)
ActivitySelection(start, finish, n)
}
/* Output
The following activities are selected:
0 1 4 6
*/
Applications
- Scheduling events in a room having multiple competing events
- Scheduling and manufacturing multiple products having their time of production on the same machine
- Scheduling meetings in one room
- Several use cases in Operations Research
