Applications for Syntax-Directed Translation

In this article, we learn about the main application of Syntax-directed Translation which is the construction of syntax trees.

Table of contents.

1. Introduction.
2. Building syntax trees.
3. The structure of a type.
4. Summary.
5. References.

Introduction.

The main application of Syntax-Directed Translation is in the construction of syntax trees. Compilers use syntax trees as an intermediate representation, using a common form of Syntax-Directed Definitions, the input string is converted into a tree.
The compiler then traverses the tree using rules that are in effect an SDD on the syntax tree rather than the parse tree.

We will look at two SDDs used to construct syntax trees for expressions. The first is S-Attributed and is suitable in cases we perform bottom-up parsing and the second is L-Attributed and is suitable during top-down parsing. The third is L-Attributed dealing with basic array types.

Building syntax trees.

Every node in a syntax tree represents a construct and the children of the node represent meaningful components of the construct.

Given a syntax tree that represents an expression E1 + E2. We have the label + and two children that represent the subexpressions.

To implement the nodes of a syntax tree we use objects with several fields. Every object will have an op field which will act as its label.
In addition to the op field, the object will also have a field that holds a lexical value for a leaf node. That is if the node is at all a leaf nod
Also, if the node is an interior node, the number of fields will be proportional to the number of children it has in the syntax tree. Here we use a constructor function Node that takes two or more arguments then creates an object with the first field op and k additional fields for the k children c1, ..., ck.

An example - S-Attributed.

We have the following S-Attributed definition. It constructs syntax trees for a simple expression grammar involving binary operators.

These operators have the same precedence level and are jointly left-associative. Non-terminals have a synthesized attribute node that represents a node in the syntax tree.
Each time the production E -> E1 + T is used, its corresponding rule creates a node with + for op and two children these are, E1.node, and T.node for the subexpression. The second production will also have a similar rule
For the third production, no node is created. This is because E.node is similar t T.node. Similarly, no node is created for the fourth production.
The value of T.node is similar to E.node and since we only use parenthesis to group them, they influence the structure of the parse tree and syntax tree.

The last final two productions have a single terminal to the right. The constructor Leaf is used to create a suitable node that will become the value of T.node.

The following is a syntax tree for an input a - 4 + x;

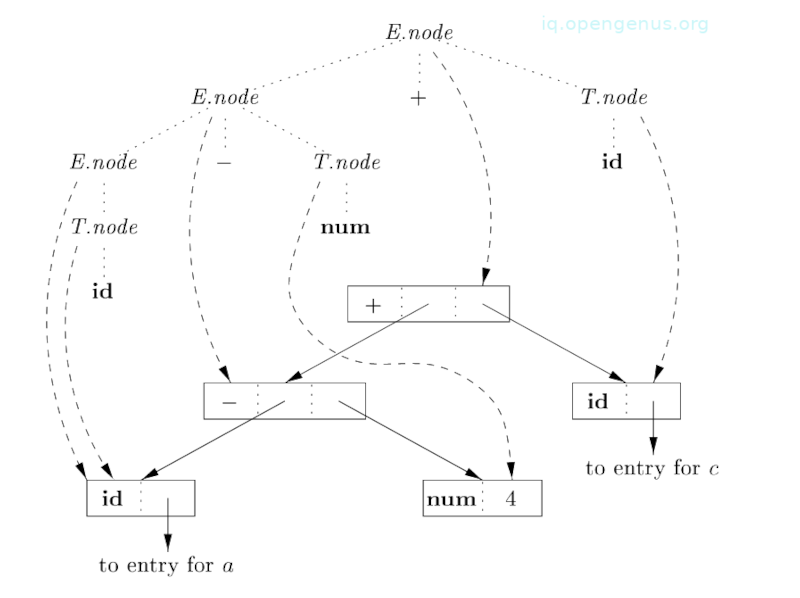
Steps involved in the construction of the above syntax tree - image 3

Nodes in the syntax tree are shown as records, they have the op field as their first field. Edges of the syntax tree are solid lines.
A parse tree is shown with dotted edges even though its construction is unnecessary.
We also have dashed lines, these represent the values of E.node and T.node. Each line points to the appropriate node in the syntax tree.

We also see leaves a, 4, and c constructed by Leaf. We assume that the lexical value of id.entry points to the symbol table, and the lexical value of num.val is a numerical value of a constant. Leaves or pointers to them become the value of T.node at the parse tree nodes that are labeled T, this is according to the fifth and sixth rules.

By the third rule, the pointer to the leaf for a is also the value of E.node for the leftmost E in the tree.

By the second rule, we create a node with op equal to the minus sign and pointers to the first two leaves. And, by the first rule, we produce a root node of the syntax tree by combining the node for the minus sign with the third leaf.

If rules are evaluated during a postorder traversal of the parse tree or with reductions during a bottom-up parse, then the sequence of steps from image 3 results int p5 pointing to the root of the built syntax tree.

Given a grammar that was designed for top-down parsing, a similar syntax tree is constructed using a similar sequence of steps even if the structure of the parse tree significantly differs from syntax trees.

An example. L-Attributed

We have the following L-attributed definition that performs a similar translation as the S-Attributed definition.

The idea is to build a syntax tree for x + y by passing x as an inherited attribute, this is because x and +y live in different subtrees. A non-terminal E' is the counterpart of a non-terminal T' as we shall come to see.

Non-terminal E' has an inherited attribute inh and a synthesized one syn. E'.inh represents the partial syntax tree that is constructed so far.
It represents the root of the tree for the prefix of the input string to the left of the subtree for E'.

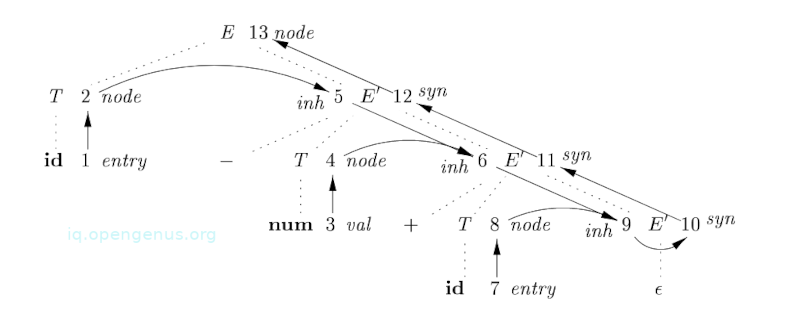
Looking at node 5 in the graph above, E'.inh denotes the root of the partial syntax tree for the identifier a, that is, the leaf for a.
At node 6, E'.inh denotes the root for the partial syntax tree for an input a - 4.
At node 9, E'.inh points to the root of the whole syntax tree.
syn attributes pass this value up the parse tree until it becomes the value of E.node. In other words, the attribute value at node 10 is defined by rule E'.syn = E'.inh that is associated with the production E' $\to ϵ$
The value of the attribute at node 11 is defined by the rule E'.syn = ${\mathrm{E}}_1^{\text{'}}$.syn that is associated with production 2 from IMAHE HERE (5.13)
Also note that similar rule also define the values of attributes at nodes 12 and 13.

The structure of a type.

When the structure of a parse tree is different from the abstract syntax of the input, inherited attributes are useful since they can carry information from one part of the tree to another.

In the following example, we see how a mismatch in a structure can be caused by the language design and not constraints on the parsing method.

An example.

In the C-programming language, type int[2][3] can be read as 'array of 2 arrays of 3 integers'. The type expression array(2 array(3, integer)), int[2][3] is shown below; - image 6

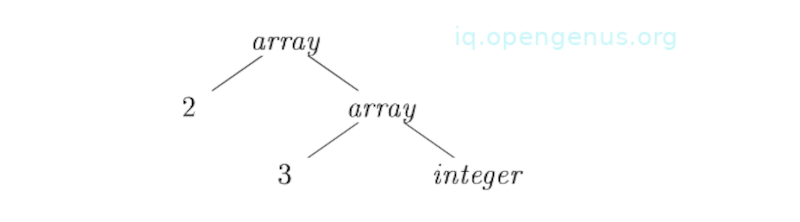
The array operator takes two parameters, the first a number and the second a type. If types are represented by trees, then this operator will return a tree node that is labeled with two children for a number and type.

We have the following SDD;

Non-terminal T generates a basic type or an array type. Non-terminal B generates one of the basic types int and float. T generates a basic type when it derives BC and derives $ϵ$. Otherwise C generates array components that consist of a sequence of integers each surrounded by a pair of brackets.

Non-terminals B and T synthesize attribute t that represents a type. Non-terminal C has two attributes, the first an inherited attribute b and a synthesized attribute t. Inherited b attributes pass a basic type down the tree and the synthesized t attributes accumulate results.

We have the following annotated syntax tree for an input string int[2][3]

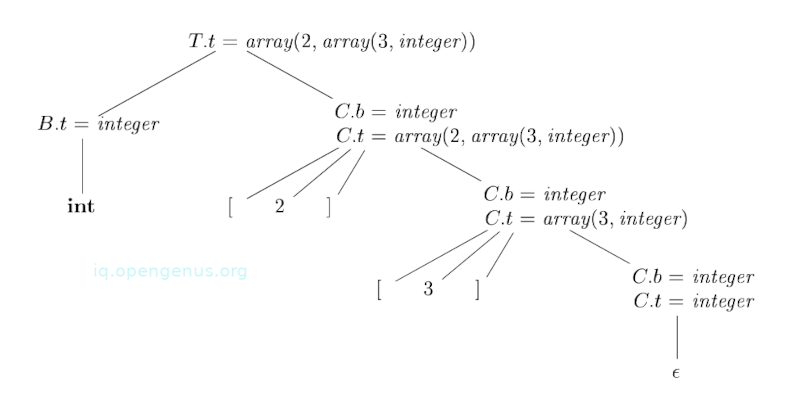
The corresponding type expression in *image 6 *is constructed by passing the type integer from B down the Cs chain through the attributes of t.
In detail at the root of T $\to$ BC, nonterminal C inherits type from B using an inherited attribute C.b. At the rightmost node for C, the production is C $\to ϵ$ therefore, C.t is equal to C.b.
Semantic rules for C $\to$ [num]C1 for C.t by applying the operator array to the operands num.val and C1.t.

Summary.

Compilers use syntax trees as intermediate representations, using a common form of Syntax-Directed Definitions, the input string is converted into a tree.
Every node in a syntax tree represents a construct and the children of the node represent meaningful components of the construct.

When the structure of a parse tree is different from the abstract syntax of the input, inherited attributes are useful since they can carry information from one part of the tree to another.

References.

Compilers Principles, Techniques, & Tools - Alfred V. Aho, Monica S. Lam