Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will briefly discuss about the Metric Travelling Salesman Probelm and an approximation algorithm named 2 approximation algorithm, that uses Minimum Spanning Tree in order to obtain an approximate path.
What is the travelling salesman problem ?
Travelling Salesman Problem is based on a real life scenario, where a salesman from a company has to start from his own city and visit all the assigned cities exactly once and return to his home till the end of the day. The exact problem statement goes like this,
"Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point."
There are two important things to be cleared about in this problem statement,
- Visit every city exactly once
- Cover the shortest path
The naive & dynamic approach for solving this problem can be found in our previous article Travelling Salesman Problme using Bitmasking & Dynamic Programming. We would really like you to go through the above mentioned article once, understand the scenario and get back here for a better grasp on why we are using Approximation Algorithms.
If you think a little bit deeper, you may notice that both of the solutions are infeasible as there is no polynomial time solution available for this NP-Hard problem. There are approximate algorithms to solve the problem though.
The approximate algorithms for TSP works only if the problem instance satisfies Triangle-Inequality.
Why are we using triangle inequality ?
So in the above instance of solving Travelling Salesman Problem using naive & dynamic approach, we may notice that most of the times we are using intermediate vertices inorder to move from one vertex to the other to minimize the cost of the path, we are going to minimize this scenario by the following approximation.
Let's approximate that,
"The least distant path to reach a vertex j from i is always to reach j directly from i, rather than through some other vertex k (or vertices)" i.e.,
dis(i, j) <= dis(i, k) + dist(k, j)
dis(a,b) = diatance between a & b, i.e. the edge weight.
The Triangle-Inequality holds in many practical situations.
Now our problem is approximated as we have tweaked the cost function/condition to traingle inequality.
What is the 2 approximation algorithm for TSP ?
When the cost function satisfies the triangle inequality, we may design an approximate algorithm for the Travelling Salesman Problem that returns a tour whose cost is never more than twice the cost of an optimal tour. The idea is to use Minimum Spanning Tree (MST).
The Algorithm :
- Let 0 be the starting and ending point for salesman.
- Construct Minimum Spanning Tree from with 0 as root using Prim’s Algorithm.
- List vertices visited in preorder walk/Depth First Search of the constructed MST and add source node at the end.
Why 2 approximate ?
Following are some important points that maybe taken into account,
- The cost of best possible Travelling Salesman tour is never less than the cost of MST. (The definition of MST says, it is a minimum cost tree that connects all vertices).
- The total cost of full walk is at most twice the cost of MST (Every edge of MST is visited at-most twice)
- The output of the above algorithm is less than the cost of full walk.
Designing the code:
Step - 1 - Constructing The Minimum Spanning Tree
We will be using Prim's Algorithm to construct a minimum spanning tree from the given graph as an adjacency matrix.
int minimum_key(int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
vector<vector<int>> MST(int parent[], int graph[V][V])
{
vector<vector<int>> v;
for (int i = 1; i < V; i++)
{
vector<int> p;
p.push_back(parent[i]);
p.push_back(i);
v.push_back(p);
p.clear();
}
return v;
}
// getting the Minimum Spanning Tree from the given graph
// using Prim's Algorithm
vector<vector<int>> primMST(int graph[V][V])
{
int parent[V];
int key[V];
// to keep track of vertices already in MST
bool mstSet[V];
// initializing key value to INFINITE & false for all mstSet
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// picking up the first vertex and assigning it to 0
key[0] = 0;
parent[0] = -1;
// The Loop
for (int count = 0; count < V - 1; count++)
{
// checking and updating values wrt minimum key
int u = minimum_key(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
vector<vector<int>> v;
v = MST(parent, graph);
return v;
}
Prim's Algorithm in Brief:
As we may observe from the above code the algorithm can be briefly summerized as,
- Creating a set mstSet that keeps track of vertices already included in MST.
- Assigning a key value to all vertices in the input graph. Initialize all key values as INFINITE. Assign key value as 0 for the first vertex so that it is picked first.
- [The Loop] While mstSet doesn’t include all vertices
- Pick a vertex u which is not there in mstSet and has minimum key value.(minimum_key())
- Include u to mstSet.
- Update key value of all adjacent vertices of u. To update the key values, iterate through all adjacent vertices. For every adjacent vertex v, if weight of edge u-v is less than the previous key value of v, update the key value as weight of u-v.
Step - 2 - Getting the preorder walk/ Defth first search walk:
We have two ways to perform the second step,
1 - Costructing a generic tree on the basic of output received from the step -1
2 - Constructing an adjacency matrix where graph[i][j] = 1 means both i & j are having a direct edge and included in the MST.
For simplicity, let's use the second method where we are creating a two dimensional matrix by using the output we have got from the step- 1, have a look at the below code to understand what we are doing properly.
int main()
{
// initial graph
int graph[V][V] = { { 0, 10, 18, 40, 20 },
{ 10, 0, 35, 15, 12 },
{ 18, 35, 0, 25, 25 },
{ 40, 15, 25, 0, 30 },
{ 20, 13, 25, 30, 0 } };
vector<vector<int>> v;
// getting the output as MST
v = primMST(graph);
// creating a dynamic matrix
int** edges_list = new int*[V];
for(int i=0;i<V;i++)
{
edges_list[i] = new int[V];
for(int j=0;j<V;j++)
{
edges_list[i][j] = 0;
}
}
// setting up MST as adjacency matrix
for(int i=0;i<v.size();i++)
{
int first_node = v[i][0];
int second_node = v[i][1];
edges_list[first_node][second_node] = 1;
edges_list[second_node][first_node] = 1;
}
// a checker function for the DFS
bool* visited_nodes = new bool[V];
for(int i=0;i<V;i++)
{
bool visited_node;
visited_nodes[i] = false;
}
//performing DFS
DFS(edges_list,V,0,visited_nodes);
// adding the source node to the path
final_ans.push_back(final_ans[0]);
// printing the path
for(int i=0;i<final_ans.size();i++)
{
cout << final_ans[i] << "-";
}
return 0;
}
Depth First Search Algorithm:
- Push the starting_vertex to the final_ans vector.
- Checking up the visited node status for the same node.
- Iterating over the adjacency matrix (depth finding) and adding all the child nodes to the final_ans.
- Calling recursion to repeat the same.
It's pretty similar to preorder traversal and simpler to understand, have a look at the following code,
// getting the preorder walk of the MST using DFS
void DFS(int** edges_list,int num_nodes,int starting_vertex,bool* visited_nodes)
{
// adding the node to final answer
final_ans.push_back(starting_vertex);
// checking the visited status
visited_nodes[starting_vertex] = true;
// using a recursive call
for(int i=0;i<num_nodes;i++)
{
if(i==starting_vertex)
{
continue;
}
if(edges_list[starting_vertex][i]==1)
{
if(visited_nodes[i])
{
continue;
}
DFS(edges_list,num_nodes,i,visited_nodes);
}
}
}
The final_ans vector will contain the answer path.
The Final Code:
#include <bits/stdc++.h>
using namespace std;
// Number of vertices in the graph
#define V 5
// Dynamic array to store the final answer
vector<int> final_ans;
int minimum_key(int key[], bool mstSet[])
{
int min = INT_MAX, min_index;
for (int v = 0; v < V; v++)
if (mstSet[v] == false && key[v] < min)
min = key[v], min_index = v;
return min_index;
}
vector<vector<int>> MST(int parent[], int graph[V][V])
{
vector<vector<int>> v;
for (int i = 1; i < V; i++)
{
vector<int> p;
p.push_back(parent[i]);
p.push_back(i);
v.push_back(p);
p.clear();
}
return v;
}
// getting the Minimum Spanning Tree from the given graph
// using Prim's Algorithm
vector<vector<int>> primMST(int graph[V][V])
{
int parent[V];
int key[V];
// to keep track of vertices already in MST
bool mstSet[V];
// initializing key value to INFINITE & false for all mstSet
for (int i = 0; i < V; i++)
key[i] = INT_MAX, mstSet[i] = false;
// picking up the first vertex and assigning it to 0
key[0] = 0;
parent[0] = -1;
// The Loop
for (int count = 0; count < V - 1; count++)
{
// checking and updating values wrt minimum key
int u = minimum_key(key, mstSet);
mstSet[u] = true;
for (int v = 0; v < V; v++)
if (graph[u][v] && mstSet[v] == false && graph[u][v] < key[v])
parent[v] = u, key[v] = graph[u][v];
}
vector<vector<int>> v;
v = MST(parent, graph);
return v;
}
// getting the preorder walk of the MST using DFS
void DFS(int** edges_list,int num_nodes,int starting_vertex,bool* visited_nodes)
{
// adding the node to final answer
final_ans.push_back(starting_vertex);
// checking the visited status
visited_nodes[starting_vertex] = true;
// using a recursive call
for(int i=0;i<num_nodes;i++)
{
if(i==starting_vertex)
{
continue;
}
if(edges_list[starting_vertex][i]==1)
{
if(visited_nodes[i])
{
continue;
}
DFS(edges_list,num_nodes,i,visited_nodes);
}
}
}
int main()
{
// initial graph
int graph[V][V] = { { 0, 10, 18, 40, 20 },
{ 10, 0, 35, 15, 12 },
{ 18, 35, 0, 25, 25 },
{ 40, 15, 25, 0, 30 },
{ 20, 13, 25, 30, 0 } };
vector<vector<int>> v;
// getting the output as MST
v = primMST(graph);
// creating a dynamic matrix
int** edges_list = new int*[V];
for(int i=0;i<V;i++)
{
edges_list[i] = new int[V];
for(int j=0;j<V;j++)
{
edges_list[i][j] = 0;
}
}
// setting up MST as adjacency matrix
for(int i=0;i<v.size();i++)
{
int first_node = v[i][0];
int second_node = v[i][1];
edges_list[first_node][second_node] = 1;
edges_list[second_node][first_node] = 1;
}
// a checker function for the DFS
bool* visited_nodes = new bool[V];
for(int i=0;i<V;i++)
{
bool visited_node;
visited_nodes[i] = false;
}
//performing DFS
DFS(edges_list,V,0,visited_nodes);
// adding the source node to the path
final_ans.push_back(final_ans[0]);
// printing the path
for(int i=0;i<final_ans.size();i++)
{
cout << final_ans[i] << "-";
}
return 0;
}
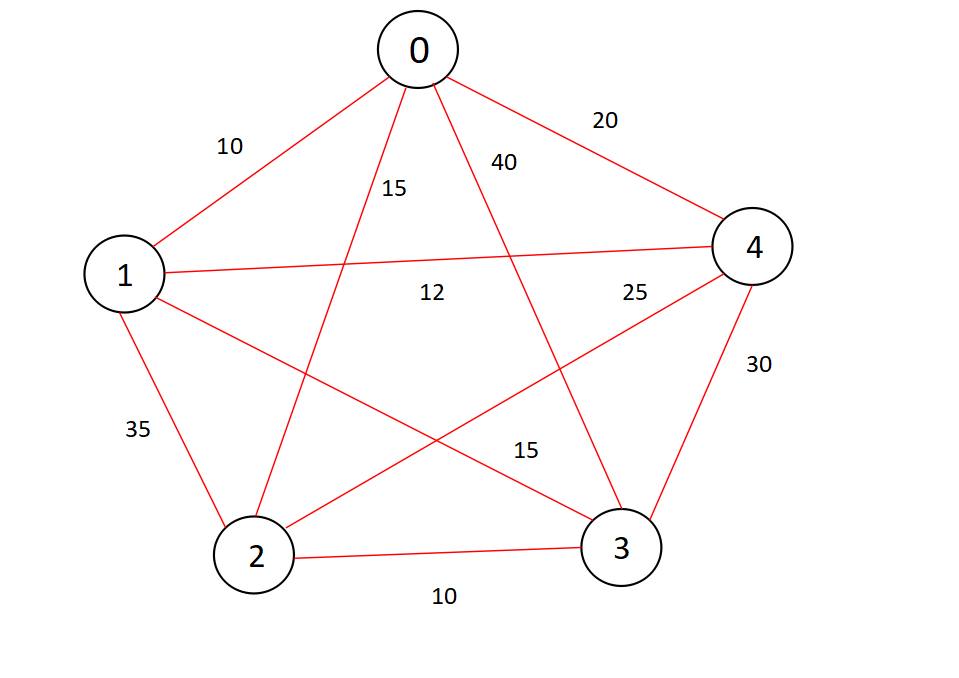
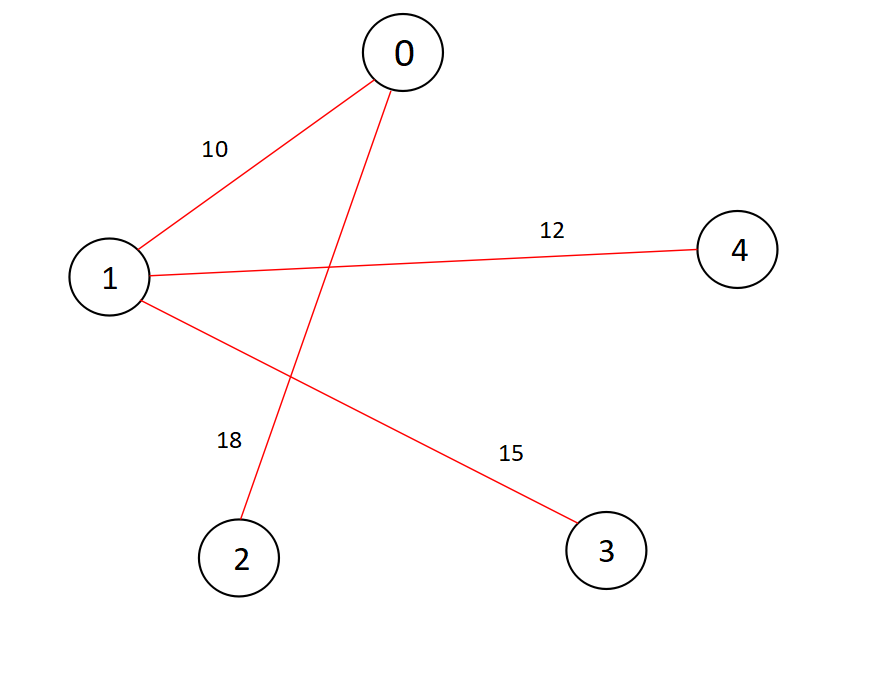
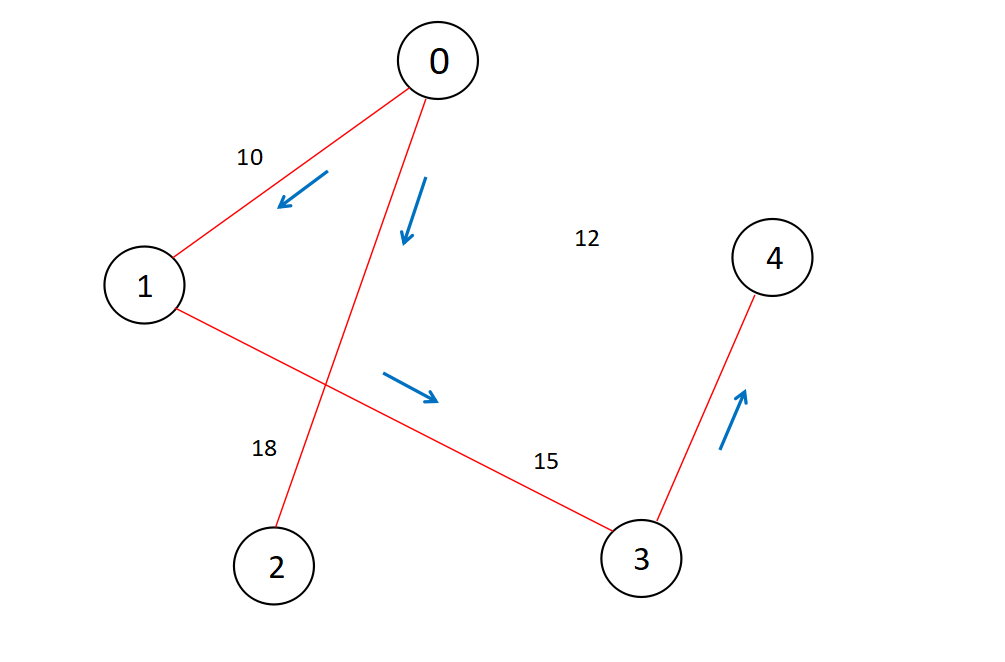
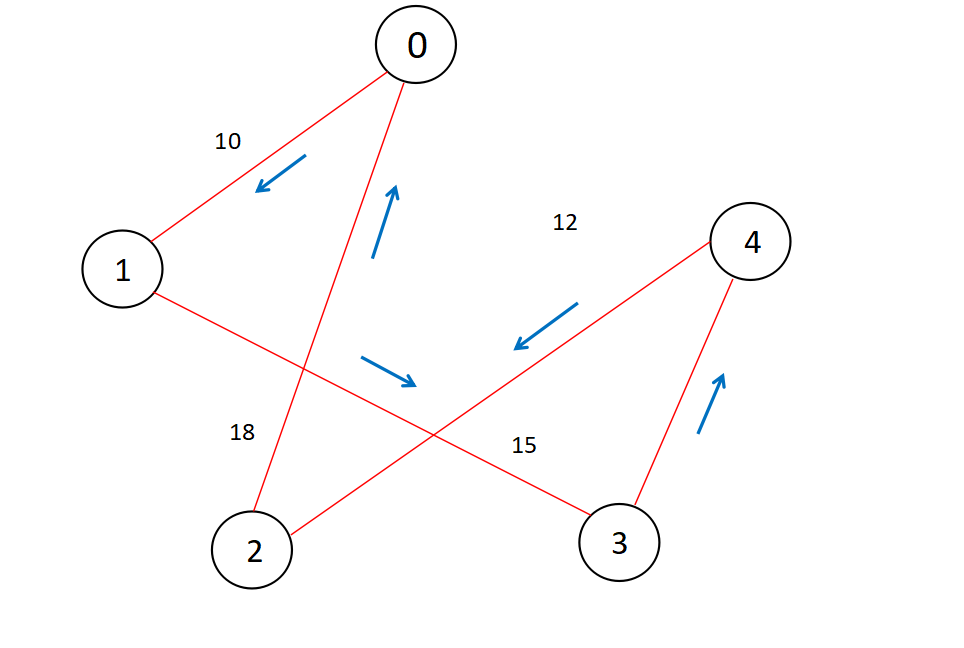
An Example:
Let's try to visualize the things happening inside the code,
Let's have a look at the graph(adjacency matrix) given as input,
After performing step-1, we will get a Minimum spanning tree as below,
Performing DFS, we can get something like this,
Final step, connecting DFS nodes and the source node,
Hence we have the optimal path according to the approximation algorithm, i.e. 0-1-3-4-2-0.
Complexity Analysis:
The time complexity for obtaining MST from the given graph is O(V^2) where V is the number of nodes.
The worst case space complexity for the same is O(V^2), as we are constructing a vector<vector<int>> data structure to store the final MST.
The time complexity for obtaining the DFS of the given graph is O(V+E) where V is the number of nodes and E is the number of edges.
The space complexity for the same is O(V).
Hence the overall time complexity is O(V^2) and the worst case space somplexity of this algorithm is O(V^2).