Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will start our discussion by understanding the problem statement of The Travelling Salesman Problem perfectly and then go through the basic understanding of bit masking and dynamic programming.
What is the problem statement ?
Travelling Salesman Problem is based on a real life scenario, where a salesman from a company has to start from his own city and visit all the assigned cities exactly once and return to his home till the end of the day. The exact problem statement goes like this,
"Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point."
There are two important things to be cleared about in this problem statement,
- Visit every city exactly once
- Cover the shortest path
What is the need of Dynamic Programming ?
If we look into the brute force approach for solving this problem, we can see that due to recursion call, a lot of cases are repeating themselves and that's the reason of a bigger runtime.
The code for the brute force approach can be found below,
class brute_force
{
public:
int shortest_path_sum(int** edges_list, int num_nodes)
{
int source = 0;
vector<int> nodes;
for(int i=0;i<num_nodes;i++)
{
if(i != source)
{
nodes.push_back(i);
}
}
int n = nodes.size();
int shortest_path = INT_MAX;
while(next_permutation(nodes.begin(),nodes.end()))
{
int path_weight = 0;
int j = source;
for (int i = 0; i < n; i++)
{
path_weight += edges_list[j][nodes[i]];
j = nodes[i];
}
path_weight += edges_list[j][source];
shortest_path = min(shortest_path, path_weight);
}
return shortest_path;
}
};
As it can be deduced easily from the above code that, the time complexity is O(n!) and the space complexity is O(n^2).
By using dynamic programming we can save the repeated cases when they are calculated for the first time, and next time when we need the result we can directly use them from our storage(in terms of data structures).
What is the need of Bit Masking ?
As you might know, computer hardwares natively support binary digits(bits) i.e. 0 for false and 1 for true. In other language we can compile that 0 means not occupied and 1 means occupied.
We can break the problem into three different parts,
- Constructing and maintaining another 2D array which stores the shortest path sum values for each (i,j), whcih means in this matrix, value at (i,j) denotes the weight of the shortest path at any instance of the program run.
- Maintaining one visited variable, which in terms denote the total possible permutations of the cities.
- Finally we will be checking if a city is visited before. We will be using bitwise & and bitwise left shift << operator to get into the solution.
Steps To Solve the Problem
There are few classical and easy steps that we must follow to solve the TSP problem,
- Finding Adjacent matrix of the graph, which will act as an input.
- performing the shortest_path algorithm with the help of bitmasking and dynamic programming, by coding out a function.
- Understanding the bitwise operators.
Step-1 - Finding Adjacent Matrix Of the Graph
You will need a two dimensional array for getting the Adjacent Matrix of the given graph. Here are the steps;
- Get the total number of nodes and total number of edges in two variables namely num_nodes and num_edges.
- Create two multidimensional arrays, edges_list having the dimension equal to num_nodes * num_nodes and dp_array having the dimension equal to total number of permutations m, which is interms equal to (1<<num_nodes). Set all the dp_array entries to -1, which will act as a check point integer in the core algorithm.
- Run a loop num_nodes time and take two inputs namely first_node and second_node * everytime as two nodes having an edge between them and place the edges_list[first_node][second_node] position equal to 1.
- Finally after the loop executes we have an adjacent matrix available i.e edges_list.
// Getting the number of nodes and number of edges as input
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
/// creating a multi-dimensional array
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
/// adjacent matrix filling mechanism
for(int i=0;i<num_edges;i++)
{
int first_node,second_node,weight;
cin >> first_node >> second_node >> weight;
edges_list[first_node][second_node] = weight;
edges_list[second_node][first_node] = weight;
}
int visited = (1<<num_nodes)-1;
int m = 1<<num_nodes;
int** dp_array = new int*[m];
for(int i=0;i<m;i++)
{
dp_array[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
dp_array[i][j] = -1;
}
}
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << edges_list[i][j] << " ";
}
cout << endl;
}
cout << endl << endl;
brute_force approach1;
dynamic_programming approach2;
cout << approach1.shortest_path_sum(edges_list,num_nodes) << endl;
cout << approach2.shortest_path_sum(edges_list,dp_array,visited,1,0,num_nodes) << endl;
return 0;
Step - 2 - Performing The Shortest Path Algorithm using Dynamic Programming and Bitmasking
The most important step in designing the core algorithm is this one, let's have a look at the pseudocode of the algorithm below. We will be considering a small example and try to understand each of the following steps.
What is a mask ?
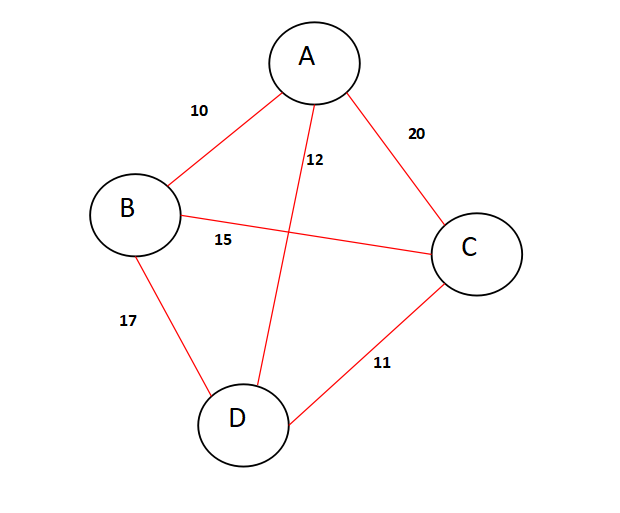
Let's consider the following graph as an example, where we have four cities named A,B,C,D and there are six weighted edges between them as shown in the figure.
So for the salesman to cover all the cities and return to the main city, he has to visit each city once. Lets consider 4 bits for A,B,C,D where 0 in a bit represents the city is not visited and 1 represented the city is visited.
So for the visited variable in the algorithm, we are considering all the citities already visited and that gives us a bit representation of
1 1 1 1. Have a look at the following diagram.
As we can see this bit representation will give use an integer representation equal to (2^4 - 1), which can be otherwise written as (1<<4) - 1. The aim of using bitwise operators like leftshift instead of using pow() etc is that, bits work on a hardware level which are faster.
This deduce our first step of assigning the visited variable a value which is equal to (1<<num_nodes)-1.
The next step is to interpret the importance of mask.
mask is nothing but a checker if all the nodes/cities are visited. Suppose the salesman starts from node A. It means the value of mask will be 0 0 0 1, which is 1 in integer format.
As soon as the salesman visits B it become 0 0 1 1.
If the salesman visits C in the second and not B then it becomes 0 1 0 1.
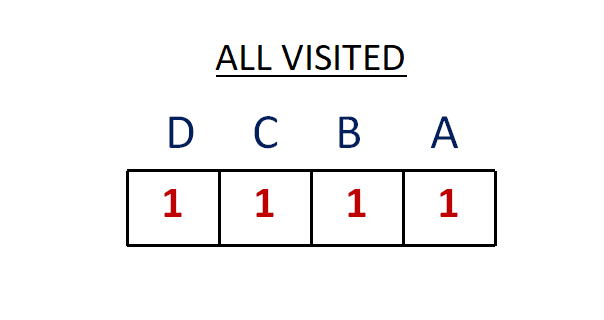
And when he visits all the cities once, we get mask same as that of visited, i.e.
1 1 1 1.
This serves as the base case of our algorithm. When the mask is equal to visited we retrun something. But what to return ? We will discuss next.
class dynamic_programming
{
public:
int shortest_path_sum(int** edges_list,int** dp_array,int visited,int mask,int position,int num_nodes)
{
if(mask == visited)
{
return edges_list[position][0];
}
if(dp_array[mask][position] != -1)
{
return dp_array[mask][position];
}
int ans = INT_MAX;
for(int city=0;city<num_nodes;city++){
if((mask&(1<<city))==0){
int newAns = edges_list[position][city] + shortest_path_sum( edges_list,dp_array,visited,mask|(1<<city), city,num_nodes);
ans = min(ans, newAns);
}
}
dp_array[mask][position] = ans;
return dp_array[mask][position] = ans;
}
};
What is the work of position here ?
The position stores the position of the salesman at any point of time. As we are starting from city A or we may call it as source city and denote it as 0 in our adjacency matrix, the initial position is 0. The sales man moves from city 0 to city 4 and returns back to 0.
The position value varies with city with every recursive call.
When our basecase is satisfied we will return the adjacency matrix value at the (position,source_city) coordinate, which signifies the direct path value between the position and the source.
The DP array and it's usages
The work of the dp_array here is to store the minimum possible path value of two nodes i and j at the array position (i,j). The -1 value works as a checker. If the value of certain (i,j) is -1 means the weight of the shortest path has not been calculated between i and j.
Here we perform another check that if the dp_array value for (mask,position) is not equal to -1 then return the original value at that position.
The sole aim of this step is to avoid repeatation that has occured during normal recursive solution.
The normal calculataion
And here comes the final normal calculation or we can say the core calculataion for this algorithm. This calculation will only take place if the base case and the check case gets false.
- We will be maintaining a variable named ans for getting the minimum path and assign it to INT_MAX at the beginning.
- We will be calling a loop from city= 0 to the city = n
- Perform a recursive call and save the output in a integer varaible named newAns.
- Later we will be getting the minimum of ans and newAns and assigning the same to the dp_array for memorization purpose.
- Finally return the dp_array value at (mask,position).
The Total Code
#include <bits/stdc++.h>
using namespace std;
class dynamic_programming
{
public:
int shortest_path_sum(int** edges_list,int** dp_array,int visited,int mask,int position,int num_nodes)
{
/// The base case
if(mask == visited)
{
return edges_list[position][0];
}
/// The check case to avaoid repeatation of the recursive call
if(dp_array[mask][position] != -1)
{
return dp_array[mask][position];
}
/// main calculation part
int ans = INT_MAX;
for(int city=0;city<num_nodes;city++){
if((mask&(1<<city))==0){
int newAns = edges_list[position][city] + shortest_path_sum(edges_list,dp_array,visited,mask|(1<<city), city,num_nodes);
ans = min(ans, newAns);
}
}
/// memorization of the recursion calculation
dp_array[mask][position] = ans;
return dp_array[mask][position] = ans;
}
};
int main()
{
/// Getting the number of nodes and number of edges as input
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
/// creating a multi-dimensional array
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
/// adjacent matrix filling mechanism
for(int i=0;i<num_edges;i++)
{
int first_node,second_node,weight;
cin >> first_node >> second_node >> weight;
edges_list[first_node][second_node] = weight;
edges_list[second_node][first_node] = weight;
}
int visited = (1<<num_nodes)-1;
int m = 1<<num_nodes;
int** dp_array = new int*[m];
for(int i=0;i<m;i++)
{
dp_array[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
dp_array[i][j] = -1;
}
}
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << edges_list[i][j] << " ";
}
cout << endl;
}
cout << endl << endl;
brute_force approach1;
dynamic_programming approach2;
cout << approach1.shortest_path_sum(edges_list,num_nodes) << endl;
cout << approach2.shortest_path_sum(edges_list,dp_array,visited,1,0,num_nodes) << endl;
return 0;
}
Time & Space Complexity
We have recursive calls here as well as loops. In fact we have recursive call inside loops.
It can be derived that the space complexity will be O(V^2) where V is the number of nodes/cities here.
For the time complexity we need to look into a little bit deeper.
As we can see we have a recurrance relation here in terms of recursion, which is a subproblem and each subproblem takes linear time to get the output,i.e. O(V * 2^V).This recursive call happens inside a loop havinbg runtime of O(V). Hence we have a total runtime of O(V^2 * 2^V), which is exponential.