Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we will start our discussion by understanding the problem statement of The Travelling Salesman Problem perfectly and then go through the naive bruteforce approach for solving the problem using a mathematical concept known as "permutation"
What is the problem statement ?
Travelling Salesman Problem is based on a real life scenario, where a salesman from a company has to start from his own city and visit all the assigned cities exactly once and return to his home till the end of the day. The exact problem statement goes like this,
"Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point."
There are two important things to be cleared about in this problem statement,
- Visit every city exactly once
- Cover the shortest path
Visualizing the problem
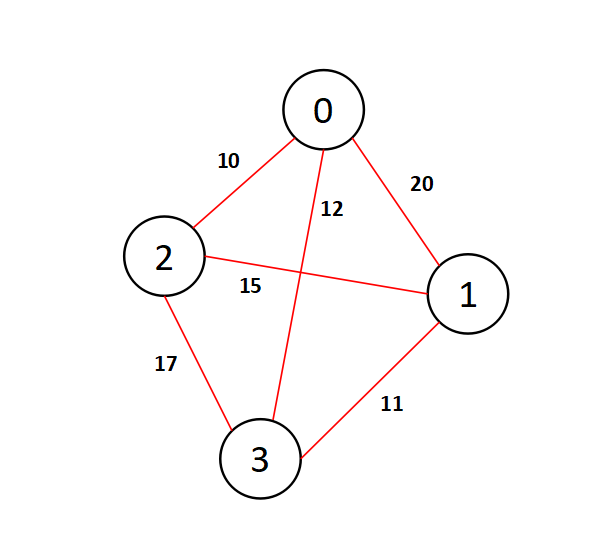
We can visualize the problem by creating a graph data structure having some nodes and weighted edges as path lengths. For example have a look at the following image,
For example - Node 2 to Node 3 takes a weighted edge of 17.
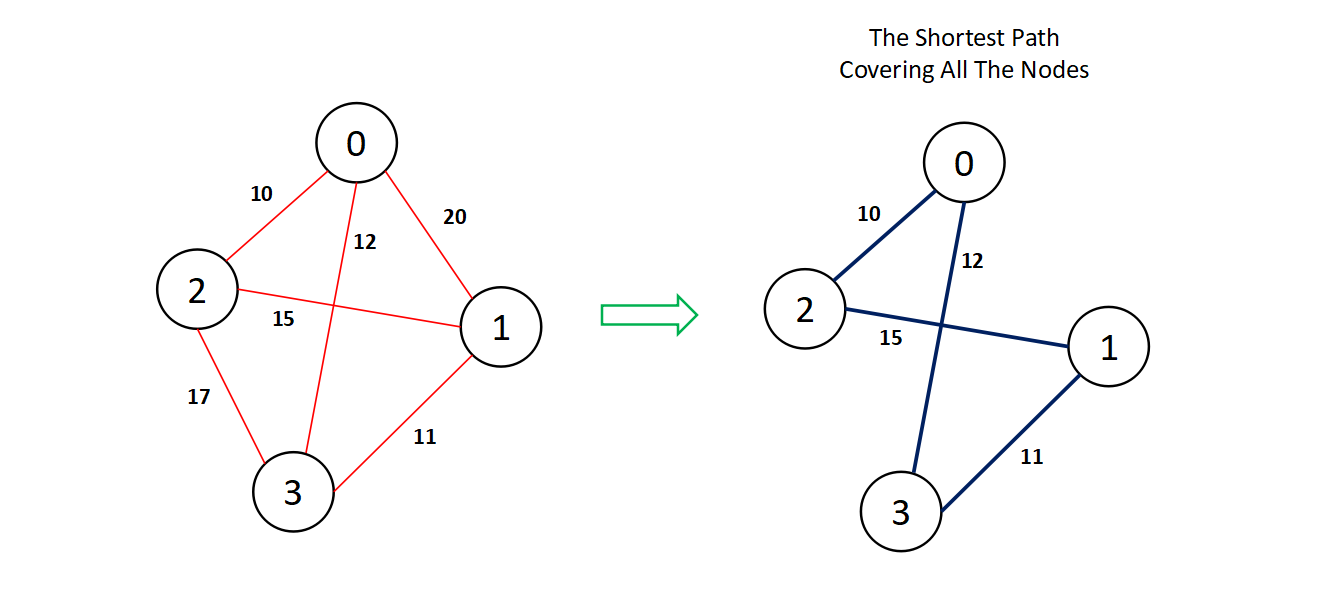
We need to find the shortest path covering all the nodes exactly once, which is highlighted in the figure below for the above graph.
Steps To Solve the Problem
There are few classical and easy steps that we must follow to solve the TSP problem,
- Finding Adjacent matrix of the graph, which will act as an input.
- performing the shortest_path algorithm, by coding out a function.
- Understanding C++ STL on using next_permutation.
Step-1 - Finding Adjacent Matrix Of the Graph
You will need a two dimensional array for getting the Adjacent Matrix of the given graph. Here are the steps;
- Get the total number of nodes and total number of edges in two variables namely num_nodes and num_edges.
- Create a multidimensional array edges_list having the dimension equal to num_nodes * num_nodes
- Run a loop num_nodes time and take two inputs namely first_node and second_node * everytime as two nodes having an edge between them and place the edges_list[first_node][second_node] position equal to 1.
- Finally after the loop executes we have an adjacent matrix available i.e edges_list.
/// Getting the number of nodes and number of edges as input
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
/// creating a multi-dimensional array
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
/// adjacent matrix filling mechanism
for(int i=0;i<num_edges;i++)
{
int first_node,second_node,weight;
cin >> first_node >> second_node >> weight;
edges_list[first_node][second_node] = weight;
edges_list[second_node][first_node] = weight;
}
Time Complexity - O(V^2), space complexity - O(V^2), where V is the number of nodes
Step - 2 - Performing The Shortest Path Algorithm
The most important step in designing the core algorithm is this one, let's have a look at the pseudocode of the algorithm below.
- Considering a starting source city, from where the salesman will strat. We can consider any city as the starting point and by default we have considered 0 as the starting point here.
- Generating the permutation of the rest cities. Suppose we have total N nodes and we have considered one node as the source, then we need to generate the rest (N-1)! (Factorial of N-1) permutations.
- We need to calculate the edge sum (path sum) for every permutation and take a track of the minumum path sum with each permutation.
- Return the minimum edge cost.
class brute_force
{
public:
int shortest_path_sum(int** edges_list, int num_nodes)
{
/// Picking a source city
int source = 0;
vector<int> nodes;
/// pushing the rest num_nodes-1 cities into a bundle
for(int i=0;i<num_nodes;i++)
{
if(i != source)
{
nodes.push_back(i);
}
}
int n = nodes.size();
int shortest_path = INT_MAX;
/// generating permutations and tracking the minimum cost
while(next_permutation(nodes.begin(),nodes.end()))
{
int path_weight = 0;
int j = source;
for (int i = 0; i < n; i++)
{
path_weight += edges_list[j][nodes[i]];
j = nodes[i];
}
path_weight += edges_list[j][source];
shortest_path = min(shortest_path, path_weight);
}
return shortest_path;
}
};
Step - 3 - Understanding next_permutation in C++ STL
It's a good practise to understand the functions from Standard Template Library on what they take as arguement, their working mechanism and their output. In this algorithm we have used a function named next_permutation(), which takes two Bidirectional Iterators namely, (here vector::iterator) nodes.begin() and nodes.end().
This functions returns a Boolean Type (i.e. either true or false).
Working Mechanism :
This function rearranges the objects in [nodes.begin(),nodes.end()], where the [] represents both iterator inclusive, in a lexicographical order. If there exits a greater lexicographical arrangement than the current arrangement then the function returns true else it returns false.
Lexicographical order is also known as dictionary order in mathematics.
The Main Code
#include <bits/stdc++.h>
using namespace std;
class brute_force
{
public:
int shortest_path_sum(int** edges_list, int num_nodes)
{
int source = 0;
vector<int> nodes;
for(int i=0;i<num_nodes;i++)
{
if(i != source)
{
nodes.push_back(i);
}
}
int n = nodes.size();
int shortest_path = INT_MAX;
while(next_permutation(nodes.begin(),nodes.end()))
{
int path_weight = 0;
int j = source;
for (int i = 0; i < n; i++)
{
path_weight += edges_list[j][nodes[i]];
j = nodes[i];
}
path_weight += edges_list[j][source];
shortest_path = min(shortest_path, path_weight);
}
return shortest_path;
}
};
int main()
{
/// Getting the number of nodes and number of edges as input
int num_nodes,num_edges;
cin >> num_nodes >> num_edges;
/// creating a multi-dimensional array
int** edges_list = new int*[num_nodes];
for(int i=0;i<num_nodes;i++)
{
edges_list[i] = new int[num_nodes];
for(int j=0;j<num_nodes;j++)
{
edges_list[i][j] = 0;
}
}
/// adjacent matrix filling mechanism
for(int i=0;i<num_edges;i++)
{
int first_node,second_node,weight;
cin >> first_node >> second_node >> weight;
edges_list[first_node][second_node] = weight;
edges_list[second_node][first_node] = weight;
}
for(int i=0;i<num_nodes;i++)
{
for(int j=0;j<num_nodes;j++)
{
cout << edges_list[i][j] << " ";
}
cout << endl;
}
cout << endl << endl;
brute_force approach1;
cout << approach1.shortest_path_sum(edges_list,num_nodes) << endl;
return 0;
}
Complexity
The time complexity of the algorithm is dependent upon the number of nodes. If the number of nodes is n then the time complexity will be proportional to n! (factorial of n) i.e. O(n!).
The most amount of space in this graph algorithm is taken by the adjacent matrix which is a n * n two dimensional matrix, where n is the number of nodes. Hence the space complexity is O(n^2).