
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we discuss attribute dependency graphs and attribute evaluation during semantic analysis phase in compiler design.
Table of contents.
- Introduction.
- Dependency graphs.
- Attribute evaluation.
- Summary.
- References.
Introduction.
Given a parse tree and an Syntax Directed Definition, we draw edges among attribute instances that are associated with each node in the parse tree to denote that the value of the attribute at the head of the edge is dependent upon the value of the tail of the edge, this is referred to as a dependency graph.
Dependency graphs.
These are used to show the flow of information among attribute instances within a parse tree.
In the graph, an edge from one attribute instance to another means that the value of the first attribute is required to compute the value of the second.
Edges are used to express constraints that are implied by the language semantic rules.
For each node in the parse tree, for example a node X, the dependency graph will have a node associated with X.
If a semantic rule is associated with a production P defines the value of a synthesized attribute A.b in terms of the value of X.c, then the dependency graph is said to have an edge from X.c to A.b. In more detail, at every node N labeled A where this production P is applied, we create an edge to attribute b at N from attribute c at the child of N that corresponds to this instance of symbol X in the body of the production.
If a semantic rule associated with a production P defines a value of an inherited attribute B.c in terms of the value X.a, the dependency graph contains an edge from X.a to B.c. For each node N that is labeled B and corresponds to an occurrence of B in the body of the production P, we create an edge to and attribute c at N from the attribute a at node M that corresponds to this occurrence of X. Keep in mind that M should be either the parent or a sibling.
An example:
We have the production;
E → + T
And the semantic rule;
E.val = .val + T.val.
For every node N that is labeled E, that has children corresponding to the body of the production, the synthesized attribute val at N is computed using values of val at the two children E and T.
Therefore a section of the dependency graph for every parse tree where this production is used will look like the image below.
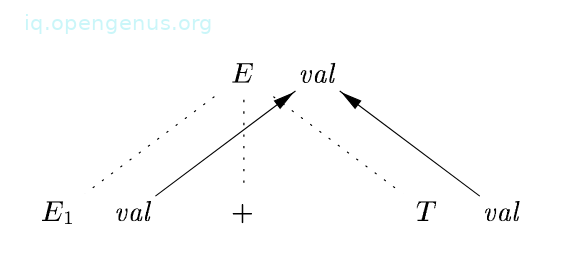
As a common convention we use dotted lines to represent the edges of the parse tree and solid lines to represent edges of the dependency graph.
An example:
We have the annotated parse tree for 3 * 5.
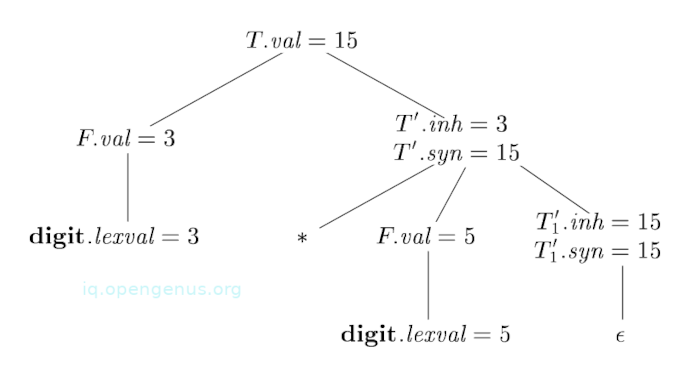
and the SDD:
| PRODUCTION | SEMANTIC RULES |
|---|---|
| T → F | .inh = F.val |
| → * F | .inh = .inh x F.val, .syn = .syn |
| → ϵ | .syn = .inh |
| F → digit | F.val = digit.lexval |
Now its complete dependency graph.
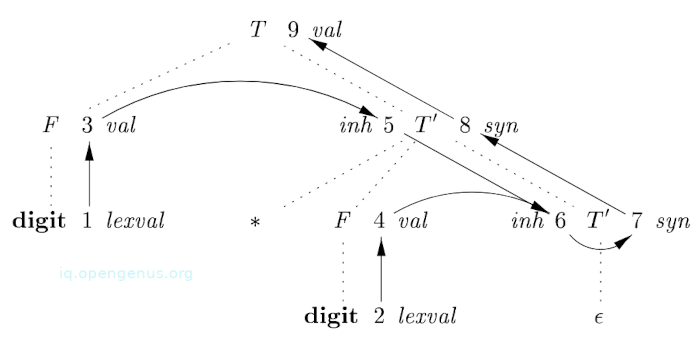
Numbers 1-9 represent nodes of the graph and correspond to attributes in the annotated parse tree for 3 * 5.
Nodes 1 and 2 represent the attribute lexval that is associated with the two leaves that are labeled digit.
Nodes 3 and 4 represent the attribute val that is associated with nodes labeled F.
Edges to node 3 from 1 and those from node 4 from 2 result from the semantic rule defining F.val in terms of digit.lexval.
As a matter of fact, F.val is equal to digit.lexval although the edges represent dependence and not equality.
5 and 6, represent the inherited attribute .inh that is associated with every occurrence of the nonterminal .
Edge(5, 3) is a result of the rule .inh = F.val that defines .inh at the right child of the root from F.val at the left child.
Edges from node 5 to 6 for .inh and from node 4 for F.val since these value are multiplied to evaluate the attribute inh at node 6.
Nodes 7 and 8 represent a synthesized attribute syn associated with the occurrences of .
Edge from 6 to 7 is a result of the semantic rule 3 associated with production 3 from the SDD.
Edge from 7 to 8 is a result of a semantic rule associated with the production 2 from the SDD.
Node 9 represents attribute T.val and the edge from 8 to 9 is a result of the semantic rule associated with production 1 from the SDD.
Attribute evaluation.
A dependency graph characterizes all possible orderings in which we can use to evaluate attributes at various nodes of a parse tree.
If the graph has an edge (M, N), then the attribute that corresponds to M is evaluated before attribute of N.
Therefore the only allowed orderings for an evaluation are the sequences of nodes , , ..., such that if there is an edge of the dependency graph from to then i < j.
This ordering embeds a directed graph into a linear ordering referred to as the topological sort of the graph.
If the graph has no cycles, then there exists at least one topological sort otherwise there are no topological sorts, that is, there is no way to evaluate the syntax directed definition(SDD) on the parse tree.
We can see why there are no cycles by finding a node with node entering edge, if there was such a node, we proceed from predecessor to predecessor until we return to the same node we have already been at, this results in a cycle. Then we mark it as the first in a topological ordering and remove it from the graph and repeat this for the remaining nodes.
An example:
Looking at the dependency graph from the previous section, we can see there are no cycles, a topological sort ordering would be in the way the nodes are numbered, that is, 1, 2, 3, ..., 9.
See how every edge goes from one node to a higher-numbered node - this is surely a topological sort.
Another topological sort would be 1, 3, 5, 2, 4, 6, 7, 8, 9.
Summary.
Dependency graphs show the flow of information among attribute instances in a parse tree.
In problematic SDDs, there are parse trees for which it is impossible to find an ordering that can be used to compute all attributes at all nodes since they have cycles.
References.
- Modern Compiler Design, Dick Grune, Kees van Reeuwijk, Henri E. Bal
- Compilers Principles, Techniques, & Tools, Alfred V. Aho, Monica S. Lam
