In this article, we will see how to divide a number using the bitwise operator >> rather than using the regular division operator / or the multiplication operator * or the modulo operator %.

Table of content:

1. Introduction to Division
2. Recap of required bitwise operations
3. Division using the left shift operator
4. Time and Space complexity
5. Conclusion

We will explore the algorithm of bitwise algorithm now.

Introduction to Division

So the task here is to divide a given number with another number and return the floor value i.e. just the decimal quotient, but we should be using bitwise operators, not the usual operators like * / % to divide the number.

let's see it with an example, consider 96 and 7
96 / 7 = 13.71 and its floor value is 13

So, we need to write a function to do this but by using the bitwise operators.

Recap of required bitwise operations

Before we jump into the problem let's make a quick recall about the bitwise shift operators because that's what we are going to use to solve this problem.

The Bitwise left shift operator

The left shift operator is used to shift the given number to the left by a certain number of bits as shown below.

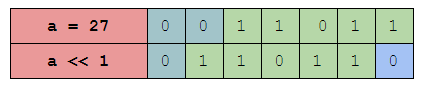
But what happens when we left shift it? let's take a closer look.

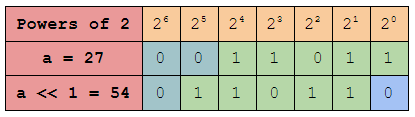
We know that the binary number system is based on powers of 2. Taking a look at the table we can see that the positional weight of each of the following bits is twice the previous bit i.e. its power is increased by 1. As a result, when we push a number towards the left by 1 bit the whole number gets multiplied by 2 power 1. Similarly when a number is pushed to the left by n bits means the number is multiplied by 2 power n.

Eg. 25 << 1 = 50 (25 * 2 power 1)
25 << 3 = 200 (25 * 2 power 3)

Thus in general if you shift a number to left by n bits, it gets multiplied n times by 2.

The Bitwise right shift operator

The right shift operator shifts the bits towards the right. This means it does the exact opposite of the left shift operator i.e. every time we shift a number towards the right by 1 bit it divides that number by 2.

Eg. 96 >> 1 = 48

Now since we have got enough idea about the shift operators let's use them to divide a number with another number.

Division using the left shift operator

Let's take two numbers a = 96 and b = 7. When we divide a by b, we are calculating how many times b is equal to a or how many b's can fit inside a. In this case, we can fit 13 b's in a i.e. a / b = 13 (Note: here we calculate only the floor value)

We know that each number can be represented as the sum of powers of 2 and also when we shift a number towards left by n bits it is multiplied by 2 power n. Thus, what we do is shift the divisor b towards the left and check if it is less than or equal to the dividend a. If it is less than or equal to the dividend we subtract it from the dividend and add the value of 2 power n to our answer. Doing so, we get our answer as the sum of powers of 2, which will give us the required quotient.

And we repeat this process for the powers of two from 31 to 0. Here we have chosen 31 because in general, the size of an integer data type is 32 bits i.e. it starts from 0 and goes till 31.

Steps

1. Initially, set the answer variable i.e. the quotient to 0.

2. Check if any one of the numbers is negative and store it in a separate variable.

3. Make both the numbers positive.

4. Start from n = 31 the most significant bit and loop till n = 0 the least significant bit.

   • Check if shifting the divisor by n bits is less than or equal to the dividend

     • if so subtract it from the dividend and update the dividend
     • Add 2 power n to the answer

     ( Note: Here the dividend is reduced to the reminder each time the condition is true. )

5. And finally, return the quotient after checking if it should be positive or negative with the result from step 2.

def bit_div(a,b):

    ans = 0 # the quotient is intialized

    neg = a < 0 or b < 0 # Checking if one of the numbers is negative

    a = abs(a) # making sure both the numbers
    b = abs(b) # are positive

    for i in range(31,-1,-1): # starting our loop

        if b << i <= a  : # checking if b multiplied by 2**i is <= a 
            a -= b << i   # subtracting b << i from a
            ans += 1 << i # adding 2 power i to the answer

    # and finally checking if the output should be negative and returning it
    return ans if neg == 0 else -1 * ans

.
Now, let's break down this code.

We get the two numbers a and b as input and then we initiate a variable ans to store our final answer i.e. the quotient. Then we check if one of the numbers is negative, but why do we do that? Because, if one of the numbers is negative the quotient is also going to be negative but, if both the numbers are positive or if both are negative the answer is going to be positive.

Then we take the absolute value of both numbers which makes them both positive. Then we begin our loop. We start from 31 the most significant bit because as said before the size of an integer is 32 bits and traverse till 0 the least significant bit. And during each iteration, we check if b << i i.e. b multiplied by 2 to the power i is less than or equal to a the dividend. If it is true we subtract b << i from the dividend a and update it and then add 1 << i which is equal to 2 power i to the answer variable ans. we do this till the loop reaches 0.

And finally, we check if the answer should be negative or positive using the variable neg's value and return it in its correct form.

Let's see it with an example to get a better understanding,

consider a = 96 and b = 7

So the control flow goes like this,

1. ans = 0
2. neg = 0 i.e. False ( since both 96 or 7 are positive )
3. Since both the numbers are positive the absolute value is the same as the number.
4. Then the loop starts from i = 31
5. Till i = 4 the if statement does not get executed since 7 << i was greater than 96.
6. When i = 3 the value of 7 << i is 56 which is less than 96 hence it goes inside the if statement.
   • a = 40 ( a = a - b << i i.e. a = 96 - 56 )
   • ans = 8 ( ans += 1 << i i.e. ans = 0 + 8 )
7. Now, i = 2 the value of 7 << i is 28 which is less than 40 the current a
   • a = 12
   • ans = 12 i.e. 8 + 4
8. Now, i = 1 again 7<<i (14) is greater than a i.e. 12 so does not execute.
9. And then i becomes 0
   • a = 5
   • ans = 13 i.e. 12 + 1
10. And the loop ends and we are left out with the reminder 5 at a and the quotient 13 in ans. Hence we finally return the quotient ans.

Time and Space complexity

The time complexity of this algorithm is going to be O((log a)^2), where a is the dividend.

This is because each left shift operation takes O(log a) time. In short, the division is based on a multiplication operation and the time complexity of the base multiplication algorithm is the time complexity of division operation.

The space complexity of this algorithm is O(1).

Conclusion

Bitwise operators are one of the important parts of any programming language. They have many applications in cryptography, hash functions, computer graphics, and so on. So having a good flow in bitwise operations is always be an asset to your programming skill.

With this article at OpenGenus, you must have the complete idea of Division using Bitwise Operations. Enjoy.