
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we discuss the design of a lexical analyzer and its role in lexical analysis, the first phase in compiler design.
Table of contents:
- Definitions.
- Generating a lexical analyzer.
- Non-deterministic finite automata.
- Deterministic finite automata.
- Structure of the generated lexical analyzer.
- Pattern matching based on NFA.
- DFAs for lexical analyzer.
- From RE to NFA to DFA.
- Implementing the lookahead operator.
- Dead states in DFA.
- Roles of the lexical analyzer.
- References.
Definitions.
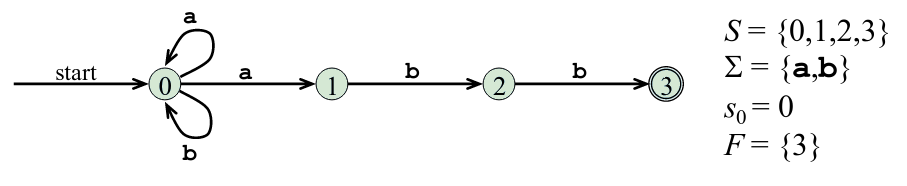
Lexical Analysis is the first phase of compiler design where input is scanned to identify tokens.
A lexeme is an instance of a token.
A token is a sequence of characters representing a unit of information in the source program.
We can either hand code a lexical analyzer or use a lexical analyzer generator to design a lexical analyzer.
Hand-coding the steps involve the following;
- Specification of tokens by use of regular expressions.
- Construction of a finite automata equivalent to a regular expression.
- Recognition of tokens by a constructed finite automata.
Generating a lexical analyzer.
A lex or flex is a program that is used to generate a lexical analyzer.
These translate regular definitions into C source code for efficient lexical analysis.
A lexical analyzer generator systematically translates regular expressions to NFA which is then translated to an efficient DFA.
NFA(Non-deterministic Finite Automata).
For any particular symbol, the machine moves to any combination of states.
It is represented by a 5 tuple set (Q, ∑, δ, q0, F) where;
Q is a finite set of states
∑ is a finite set of symbols called alphabets
δ is the transition function where δ: Q × ∑ → 2Q
belongs Q is the start state
F ⊆ Q is the set of accepting (or final) states
Graphically,
Vertices represent states.
Labeled arcs with input alphabet show the transitions.
Initial states are denoted by an empty single incoming arc.
The final state is indicated by double circles.
DFA(Deterministic Finite Automata).
This is a special case of NFA where no state has an ε-transition and for each state s and input symbol a, there exists at most one edge labeled a leaving s.
Each entry in the transition table will be a single state, that is, at most one path exists to accept a string.
Structure of the generated analyzer.
The lexical analyzer comprises of a program to simulate automata and 3 components created from the lex program by the lex, these are, a transition table for the automaton, functions passed directly through lex to the output and actions from the input program which appear as fragments of code to be invoked by the automaton simulator at the appropriate time.
A transition graph is an equivalent way of representing an NFA, for each state s and an input symbol x(and ε), the set of successor states x leads to from s.
The empty set φ is used where there is no edge labeled x from s.
A transition table is the mapping of δ of an NFA.
δ(0, a) = {0, 1}
δ(0, b) = {0}
δ(1, b) = {2}
δ(2, b) = {3}
⇓
| State | Input a | Input b |
|---|---|---|
| 0 | {0, 1} | {0} |
| 1 | {2} | |
| 2 | {3} |
A drawback of transition tables is that they tend to grow to very large sizes especially if most entries are empty sets φ which don't take any space in the transition graph.
Construction of an automaton begins by taking each regular expression pattern in the lex program and converting it to a NFA.
An NFA accepts an input string x iff there is some path with edges labeled with symbols from x in a sequence from start start to an accepting state in the transition graph.
The result is a single automaton which will recognize lexemes matching any patterns in the program so that we can combine all NFAs into one by using a new start with e-transitions for each of the start states of the NFSs.
Pattern matching based on NFAs.
Assume a lexical analyzer simulates an NFA as shown below;
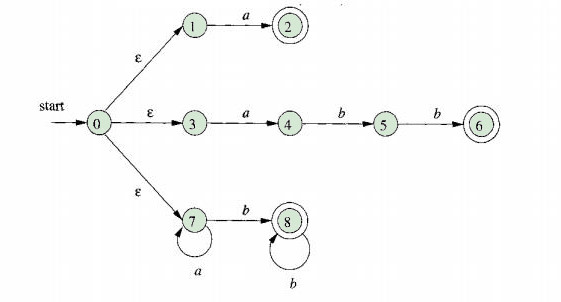
It will read input from lexemeBegin and as it moves the forward pointer ahead in the input, It will calculate the set of states it is in at each point.
When the simulation reaches a point where there are no states remaining it will determine the longest prefix that is a lexeme matching a pattern.
This is because there will be no longer prefix of an input that will get the NFA to an accepting state because the will be no more states at this point.
To determine the longest prefix, we look backwards in the sequence of sets of states until we find a set including one or more accepting states.
If there is a case where there are several such states, we select the one associated with the earliest pattern in the list from the lex program.
To do this we move the forward pointer to the end of the lexeme and perform the action associated with patterns .
DFAs for lexical analyzer.
Here we convert the NFA for all patterns into an equivalent DFA.
If there exists one or more accepting NFA states within each DFA, we determine the first pattern while accepting state is represented and make it the output of the DFA state.
The DFA lexical analyzer will simulate the DFA until a point where there is no next state after which it will back up through the sequence of states entered until an accepting state where an action associated with the pattern for that state is performed.
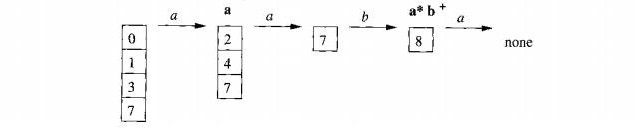
Consider the image below.
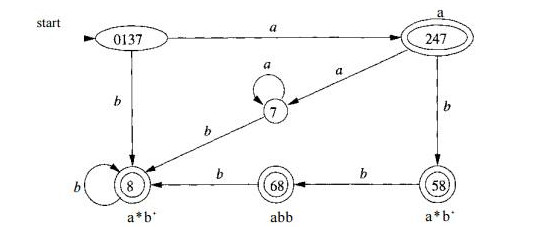
Suppose the DFA is given the input abba, the sequence of states entered will be 0137, 247, 58, 68.
At the final a, there won't be a transition out of state 68 therefore we consider the sequence from the end.
68 is an accepting state that reports the pattern p2 = abb.•
From Regular Expression to NFA to DFA.
From Regular expression to NFA
We use thompson's construction to determine a finite automaton from a regular expression.
To do this we reduce the regular expression to the smallest regular expressions and convert to NFAs then finally to DFAs
Case 1.
For a regular expression 'a', we construct the following FA
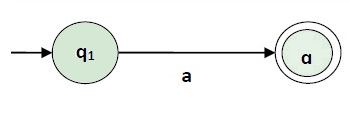
The finite automata for RE = 1
Case 2.
For a regular expression 'ab', we construct the following Finite automata,

Finite automata for RE = ab
Case 3.
For regular expression (a+b) we construct the following FA
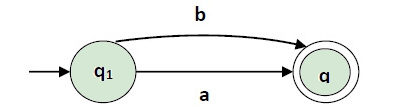
Finite automata for RE = (a+b)
Case 4.
For a regular expression (a+b)* .We construct the following finite automata
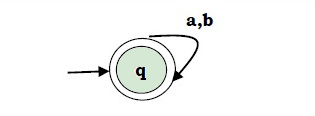
Finite automata for RE = (a+b)*
Generally; We first construct an NFA with null moves from the given regular expression and then remove the null transition from NFA and convert it to its corresponding DFA
From NFA to DFA.
Steps involved are
- Let Q' be a new set of states of the DFA and T' be the new transition table of the DFA.
- Add start state of the NFA to Q' and add transitions of the start state to the transition table T'.
If start state makes a transition to multiple states for some input alphabet, we treat the multiple states as a single state in the DFA. - If a new state is present in the transition table T', we add the new state in Q' and add the transitions to table T'.
- We repeat step 3 until no new state is present in the transition table T'.
The transition table obtained is the transition table for the required DFA.
An example:
Given the NFA,
We first construct the transition table as follows,
| State | 0 | 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | {q1, q3} | q1 |
| q2 | q2 | {q1, q2} |
We obtain δ' transition for state q0
δ'([q0], 0) = [q0]
δ'([q0], 1) = [q1]
The δ' transition for state q1 is obtained as
δ'([q1], 0) = [q1, q2] (new state)
δ'([q1], 1) = [q1]
The δ' transition for state q2 is obtained as:
δ'([q2], 0) = [q2]
δ'([q2], 1) = [q1, q2]
We obtain δ' transition on [q1, q2].
δ'([q1, q2], 0) = δ(q1, 0) ∪ δ(q2, 0)
= {q1, q2} ∪ {q2}
= [q1, q2]
δ'([q1, q2], 1) = δ(q1, 1) ∪ δ(q2, 1)
= {q1} ∪ {q1, q2}
= {q1, q2}
= [q1, q2]
The state [q1, q2] is the final state because it contains the final state q2 and the transition table for the DFA is
| State | 0 | 1 | |
|---|---|---|---|
| →[q0] | [q0] | [q1] | |
| q1 | q2 | [q1, q2] | |
| [q1, q2] | [q1, q2] | [q1, q2] |
Since q2 is an unreachable state(dead state), we eliminate it.
Implementing the lookahead operator.
Given the pattern rVr2, the . operator is necessary because the pattern r * i for a particular token may need to describe trailing context r2 inorder to identify the lexeme.
/ operator is treated as e during conversion the pattern rVr2 to an NFA, therefore we don't look for / in the input.
If the NFA recognizes the prefix xy of the input buffer matching this regular expression, the end of the lexeme wont be where the NFA enters the accepting state, rather the end occurs when the NFA enters a state s such that.
- s has an e-transition on the /(imaginary)
- there exists a path from start state to s that spells out x
- There exists a path from state s to the accepting state that spells out y.
- x is as long as possible for any xy satisfying all the above conditions.
If there is one e-transition state on the / in the NFA, then then end of the lexeme occurs when this state is entered for the last time.
If the NFA has multiple e-transition states, finding the correct state becomes difficult.
Given the pattern for the Fortran IF with lookahead
IF( condition ) THEN
We have the NFA

The e-transition from state 2 to 3 represents the lookahead operator.
State 6 indicates the presence of the keyword IF.
Also by scanning backwards to the last occurrence of state 2, we find lexeme IF whenever state 6 is entered.
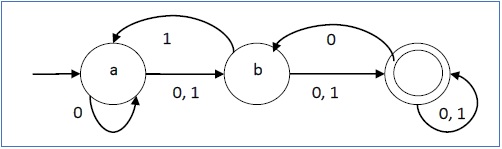
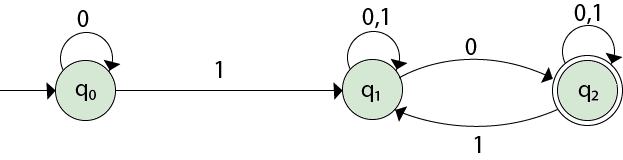
Dead states in DFA's.
These are the states from which no final state is reachable.
Once the machine enters this state, there is no way for it to reach an accepting state, therefore we expect a rejection.
Consider the image

Note that the DFA has a transition from every state on all input symbols in the input alphabet.
We have omitted transitions to the dead state 0 and therefore omitted transitions from the dead state to itself on all inputs.
To construct a DFA for use in a lexical analyzer, we treat dead states differently.
We omit transitions to the dead state and thus eliminating dead states themselves.
An NFA-DFA construction will yield several states that cannot reach an accepting state, this makes the problem harder as we must know when any of the states have been reached.
We solve this problem by combining all these states into one dead state so identification becomes easier.
Based on the two approaches, NFAs approach and DFAs, DFAs is used implementation for the lex.
Roles of lexical analyzer.
- Correlation of error messages with the source code.
- Removal of white spaces and comments from source program.
- Expansion of macros if found in source program.
- Identification of tokens.
- Reading of input characters from source program.
References.
- Modern Compiler Implementation in C by Andrew W.Appel, Chapter 2.
- Thompson's construction: (PDF) Notes by Y Manoj Kumar at IIT, Kharagpur



