
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explained the idea of Cayley’s formula which is used to find the number of trees with N nodes and M connected components. We have presented an implementation to calculate Cayley’s formula.
Table of contents:
- Introduction to Cayley’s formula
- Generalizations of Cayley’s formula
- Implementation of Cayley’s formula
Introduction to Cayley’s formula
Let us say you were given n nodes and you were asked to find out how many trees you can form with the given nodes. How would you do it?
The first idea would be to draw all the possible trees. Well, this approach might help if you were given 4 or 5 nodes, but what if you were given a 100 nodes?
At this point, its simple to just cheat!
To cheat you must know Cayley’s formula.
Cayley's formula states that the number of labeled trees on n nodes is nn-2.
Simply put, the number of trees formed with the n nodes is nn-2. Keep in mind, the trees are not isomorphic.
Wait! what do you mean by isomorphic?
Two trees are said to be isomorphic when a tree can be converted into another tree through a series of flips. To explain with an example, lets say there are two nodes, so there is only one way we can form a tree, joining the nodes a and b by a single edge, a is joined to b. Now, if we flip the tree, we have b joined to a. We say that these trees are isomorphic.
Lets understand the formula even more. Cayley’s formula tells us the count of labelled trees. Why labelled trees? Lets say if the nodes are not labelled, the number of trees would reduce since there would be no different permutations. For n=4, we would have only 2 unlabelled trees, they are
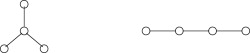
But if the trees are labelled, we would be having 44-2 = 16 trees, they are
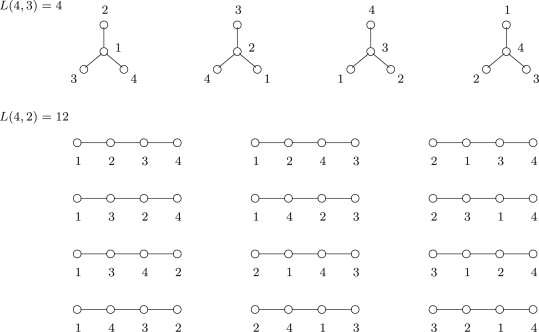
Cayley's formula allows us to find more permutations in a given set of nodes. The main thing to understand in Cayley's theorem is how the isomorphism works. For that, instead of looking them as trees, look at them as graphs, that would allow us to visualize the nodes more clearly to understand if a pair of trees are already isomorphic.
There are a lot of theorems that can prove Cayley's formula. We can prove it using Prüfer Code, Kirchhoff's matrix tree theorem, and many others. We will not be diving into the proof since it is requires some understanding of advance discrete math. Though understand, whenever you need to find the number of labelled trees from a given set of nodes, Cayley's theorem is the fastest approach. And also, we can find the number of spanning trees in a fully connected graph, Cayley's theorem can be used, since there is an edge between every pair of vertices, that edge can be used as an edge in the tree.
Generalizations of Cayley’s formula
Well let's explore the formula a bit more. Lets use the formula for labelled forests.
Let Tn,k be the number of labelled forests where
- n is the number of labelled vertices
- k is the number of connected components
- vertices 1,2,3,....k belong to different connected components
Then, T(n,k) can be defined as
Tn,k = k*nn-k-1
Implementation of Cayley’s formula
Lets write a small snippet of code to implement the above formula in python. Before you look at the code, this is the ADT of the Graph data structure we would be assuming and some helper functions that are abstracted
- The graph is implemented as an Adjacency list
- G.vertex_count(): Returns the number of vertices
- G.connected_components(): Returns the number of connected components in the graph. Keep in mind, we can find the connected components of a graph using a simple depth first search.
import math
def labelled_forests(n,k):
# Compute the value using Cayley's formula
result = k*math.pow(n, n-k-1)
return result
if __name__=="__main__":
graph = Graph()
# Find vertices and connected components
n = graph.vertex_count()
k = graph.connected_components()
ans = labelled_forests(n,k)
print(ans)
The time complexity would be logarithmic for the above code since we used the power() function which computes exponentials in logarithmic time.
The space complexity would be constant since we have not used any new variables.
Time Complexity: O(log(n))
Space Complexity: O(1)
With this article at OpenGenus, you must have a strong idea of Cayley’s formula.
