
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article we discuss a machine and paradigm-independent processing of intermediate code by recursive and iterative interpreters.
Table of contents.
- Introduction.
- Interpreters.
- Recursive Interpreters.
- Iterative Interpreters.
- Summary.
- References.
Introduction.
Processing intermediate code involves choosing between little preprocessing which is followed by execution on an interpreter or a lot of preprocessing(machine code generation) followed by the execution of the generated code on the hardware.
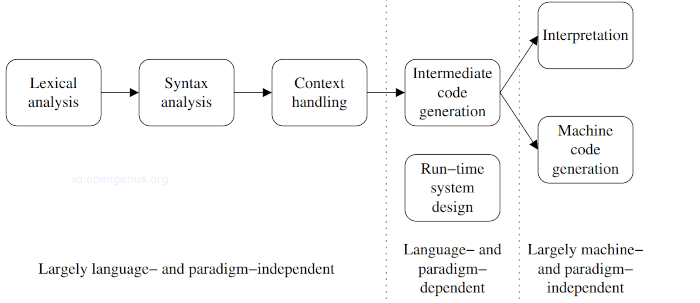
An interpreter does not require all language features to be removed and thus for example it can interpret a for-loop node directly or if an interpreter integrates intermediate code generation and target code generation, the for-loop subtree will be rewritten directly to target code.
In this article we discuss the two types of interpreters.
Interpreters.
An interpreter is the simplest way to have actions expressed by a source program to be performed. This is done by processing the AST.
An interpreter considers nodes of the AST in the correct order and performs the prescribed actions for those nodes by the language semantics.
Unlike compiling, this requires inputs to be present.
Ideally interpreters work just like CPUs, the difference is that while CPUs work on instruction sets, interpreters work on ASTs.
Interpreters can either be:
- recursive - working directly on the AST thus less preprocessing
- iterative - working on a linearized AST.
Recursive Interpreters.
A recursive interpreter will have a routine for each node type in the AST. These routines call other similar routines.
This is possible since the meaning of language constructs is defined as a function of the meaning of its components. i.e The meaning of an if-statement is defined by the meaning of the condition, the then-part and the else-part including a short paragraph in the manual tying them together.
An example
procedure ExecuteIfStatement (IfNode):
Result ← EvaluateExpression (IfNode.condition);
if Status.mode != NormalMode: return;
if Result.type != Boolean:
error "Condition in if-statement is not of type Boolean";
return;
if Result.boolean.value = True:
−− Check if the then-part exists:
if IfNode.thenPart != NoNode:
ExecuteStatement (IfNode.thenPart);
else −− Result.boolean.value = False:
−− Check if the else-part exists:
if IfNode.elsePart != NoNode:
ExecuteStatement (IfNode.elsePart);
From the above routine it can be see that, the condition is first interpreted then depending on the outcome, the then-part or else-part is interpreted.
The then and else parts can contain if-statements, therefore the routine for if-statements will be recursive.
Uniform self-identifying data representation is an important ingredient in recursive interpretation.
An interpreter has to manipulate data values defined in the program being implemented but the types and sizes of these are not known when the interpreter is being written and this makes it necessary to implement these values as variable-size records which specify the type of the run-time value, size and value itself in the interpreter. A pointer to this record will server as the 'value' during interpretation.
The image below shows how a value of type Complex_Number is seen by the programmer.

The image below show how the same value is seen by an interpreter.
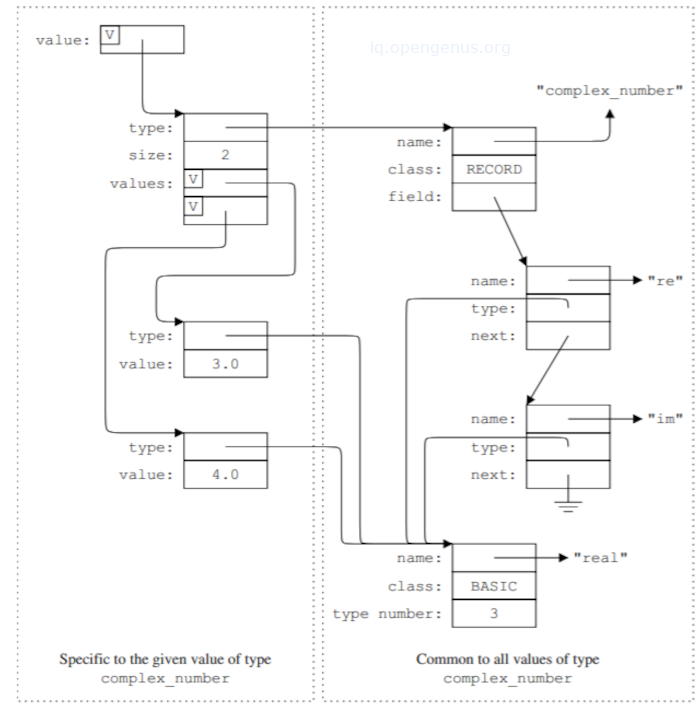
V corresponds to the run-time values, each of which is self-identifying through its type field.
The data representation consists of two parts, the value-specific part providing the actual value of the instance and the common part describing the type of value common to all values of type Complex_Number.
The status indicator is another feature of recursive interpreters, it directs flow of control.
Its primary component is the mode of operation which is an enumeration value, the normal value is NormalMode which indicates sequential flow of control, other values are also available e.g to indicate jumps, function returns, exceptions etc.
It's second component is a value which supplies more information about the non-sequential flow of control. It can be a value for ReturnMode, an exception name plus possible values for ExceptionMode and a label for JumpMode.
It also contains the file name and line number of text where it was created.
It can also hold other debugging information.
Each routine will check with the status indicator to determine how to proceed. i.e If it is in NormalMode the routine proceed normally, otherwise checks how to handle to current mode, if it can, it handles it otherwise it lets parent routines handle it.
From the previous example, the evaluation of the condition can terminate abnormally which causes ExecuteIfStatement to return immediately.
The result may be of a wrong type, if so an error is issued and it returns. The error routine responsible will either terminate interpretation or composes a ErroneousMode status indicator.
If we have a correct Boolean value, we interpret the then-part or else-part and leave the status indicator. If both parts are absent, no action is required, the status indicator is in NormalMode.
Iterative Interpreters.
The structure of iterative interpreters is much closer to the CPU. It consists of a flat loop over a case statement containing a code segment for each node type of the AST.
It runs the code segment for the node pointed to by the active-node pointer, in the end, the current code sets the active-node pointer to the next node.
The active-node pointer can be compared to the instruction pointer in the CPU.
An example
while ActiveNode.type != EndOfProgramType:
select ActiveNode.type:
case ...
case IfType:
−− We arrive here after the condition has been evaluated
−− the boolean result is on the working stack.
Value ← Pop (WorkingStack);
if Value.boolean.value = True:
ActiveNode ← ActiveNode.trueSuccessor;
else −− Value.boolean.value = False:
if ActiveNode.falseSuccessor != NoNode:
ActiveNode ← ActiveNode.falseSuccessor;
else −− ActiveNode.falseSuccessor = NoNode:
ActiveNode ← ActiveNode.successor;
case ...
The above is an outline of the main loop of an iterative interpreter. As we can see it contains a single case statement that selects the proper code segment for the active node based on type. In this case we have one code segment - for the if statements.
The condition code has been evaluated since it precedes the if node in the threaded AST. The type of condition is not checked since the full annotation has done full type checking. Calling the interpreter for the proper branch is replaced by correctly setting the active-node pointer.
Data structures here are similar to those in a compiled program than those for recursive interpreters. They include an array holding the global data if source language allows arrays, if it is stack-oriented, a stack is maintained which will hold local variables, the stack also holds stacking and scope information. It is implemented as an extensible array.
A symbol table if used is used to give better error messages.
Iterative interpreters store a lot of run time information inside a program as compared to a compiled program but less than its recursive counterpart.
While a recursive interpreter maintains an arbitrary amount of information for a variable by storing it in the symbol table, an iterative interpreter will only have a value at a given address.
A shadow memory in the form of arrays parallel to the maintained memory arrays of the interpreter remedies this situation.
Each byte in the shadow array will hold properties of the corresponding byte in the memory array.
Shadow data can be used for interpret-time checking e.g detecting use of uninitialized memory, incorrectly aligned data access and other issues.
A pro of shadow memory is that it can be easily disabled when one needs faster processing.
Some iterative interpreters store ASTs in a single array, for example because it makes it easier to write to a file which in turn allows programs to be interpreted more than once without recreation of the AST from the source text every time.
Also a more compact representation is possible this way.
Constructing an AST puts the successor of a node right after that node and if this happens oftenly, it is much better to omit the successor pointer from nodes and appoint the node following a node N as the successor of N.
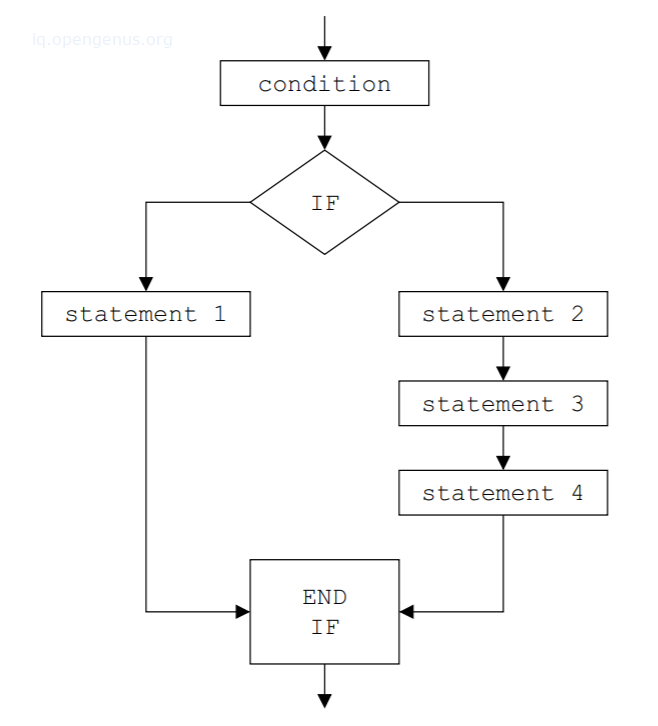
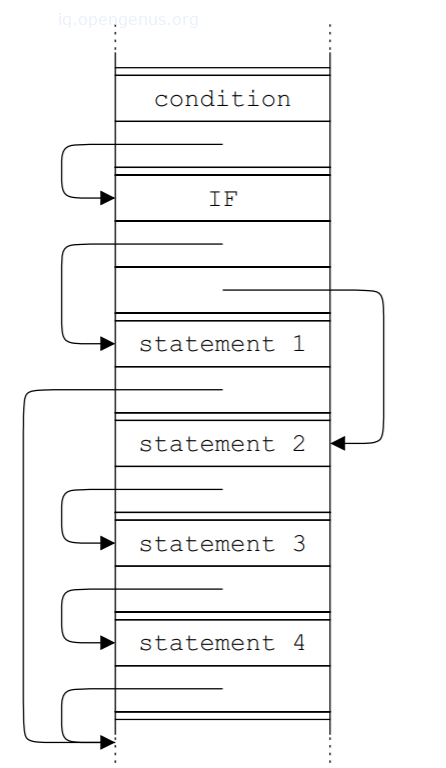
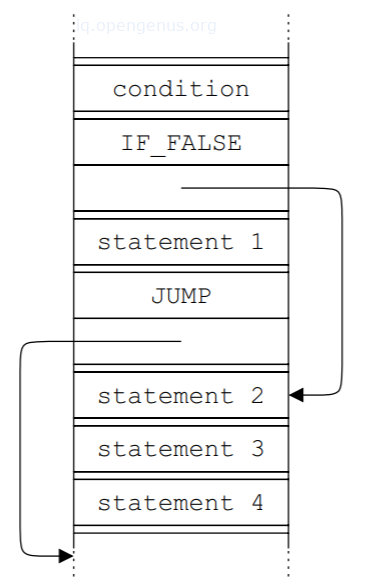
Forms of storing ASTs
Storing AST as a graph.
Storing AST in an array.
Storing AST as pseudo-instructions.
Summary.
An interpreter considers nodes of an AST orderly and performs actions defined by those nodes prescribed by the language semantics.
Interpreters can be recursive or iterative, the former has an routine for each node type in the AST, the latter consists of a flat loop over a case statement containing a code segment for each node type.
Since a recursive interpreter can be written quickly it is used for rapid prototyping
Interpreted code is much slower than compiled.
References.
- Compilers Principles, Techniques, & Tools, by A.V.Aho, R.Sethi & J.D.Ullman, Pearson
Education - Principle of Compiler Design, A.V.Aho and J.D. Ullman, Addition – Wesley
- Modern Compiler Design 2nd Edition Dick Grune • Kees van Reeuwijk • Henri E. Bal
