
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we discuss the logic programming model which finds many application areas involving facts and computing relations between them.
Introduction.
Logic programming is a computer programming paradigm based on logic where program statements express facts and rules about a problem within a system of formal logic.
Examples of logic programming languages are, Prolog, Datalog, Alice, Ciao, ASP, Twelf.
It is based on the specification of a relationship between terms, facts and using these, together with rules for inference new facts can be generated from existing facts.
Logic programming enables one to request specific inferred facts by executing queries which are obtained by the program by searching through clauses and combining them in various ways, when these combinations don't produce the correct results, backtracking is performed.
From this search variables in the rules may be bound to terms, these bindings will have to be undone during backtracking.
These terms may be constants, structures(may hold bound/unbound or other structures), and variables.
This binding is done through unification
Pros
Logic programming expresses knowledge independent of implementation.
Programs are more flexible, compressed and can be understood,.
It's use extends beyond computational disciplines as it relies on reasoning and a precise meaning of expressions.
It can be naturally changed so as to support special forms of knowledge such as meta-level or higher-order knowledge.
Logic programming enables knowledge to be separated from its use and therefore it is machine architecture independent.
Cons
Users(programmers) prefer overly operational machine operated programs.
There is no way of representing computational concepts found in built-in mechanisms of state variables.
Computation verses deduction.
To understand logic programming, we shall first see the differences between a computation and a deduction.
Computation
To compute we start from the given expression and according to the fixed set of instructions(program) we can generate a result.
An example
15 + 26 -> (1 + 2 + 1)1 -> (3 + 1)1 -> 41.
Computation is mechanical and requires no ingenuity.
Deduction
To deduce we start from a conjecture and according to the given set of rules(axioms, inference rules) we try to construct a proof of the conjecture.
An example
for n > 2,...357 years of hard work...,QED.
The logic programming model.
Logic programming is based on named relations between terms, facts stating these relations and inference rules for new facts which come from established facts.
A fact consists of the name of the relation and its terms in a syntactic notation.
e.g a binary relation, parent/2 means the relation is named parent and governs 2 terms.
e.g a unary relation, parent/1 which governs 1 term.
Examples of facts with binary relations
parent(john doe)
parent(one two)
A query could be, ?-parent(x, doe) where by x is an unbound variable.
The above query asks the system to scan and find facts matching the query then shows the values of the variables for which the matches occur.
The body of the query is the goal of the search and a fact matches a goal if there is a binding for the variables in the goal. Therefore the goal in this case results in one successive binding X = john.
It is conventional for variable names to begin with a capital letter and constants with a small letter.
Unlike facts which may contain variables, queries don't need to and this feature is useful for expressing a fact like equal(X, X) which states that X equal X for any value of X.
Example of a rule
grandparent(X, Z) :- parent(X, Y), parent(Y, Z)
:- is the head of the rule and the following part is the body of the rule.
The above rule means that after establishing the facts parent(X, Y) and parent(Y, Z) for value X, Y, Z, we infer the fact grandparent(X, Z).
We can also interpret it as replacing the goal grandparent(X, Z) by the goal list parent(X, Y), parent(Y, Z) for any X, Y, Z bindings.
Inference mechanism.
The inference technique is as follows;
We have the query ?-grandparent(john, X) which asks for X of which john is a grandparent and makes grandparent(john, X) the initial goal.
The system will try to find/infer the goal for some binding of X.
The clause grandparent(X, Z) :- parent(X, Y), parent(Y, Z) is used as a rule for inference.
We therefore make a copy with fresh variables
grandparent(X1, Z1) :- parent(X1, Y1), parent(Y1, Z1) and try to make the goal grandparent(john, X) clause and its head equal by binding the variables in them.
This is called a unification process, we shall discuss it in the next section.
The clause copy is now
grandparent(john, X) :- parent(john, Y1), parent(Y1, X).
We replace the goal grandparent(John, X) by the new goal list
parent(john, Y1), parent(Y1, X)
Then we unify the parent(john, Y1) with a fact parent(john doe) by using the binding X=doe.
The answer to the query is grandparent(john, doe).
Unification.
The simplest form of unification involves constants and variables as we have seen however there are three more possibilities namely;
- Unification between two constants succeeds if both constants are equal otherwise fails.
- Unification between two unbound variables where the variable in the head is bound to the one in the goal succeeds.
- Unification between unbound variables and constants, the unification succeeds if the constant is bound to the variable.
Unifying of structures, lists and sets.
A structure is a named list of a fixed number of components also called functor.
E.g, times(2, X) is an example of a structure with name times and components 2 and X.
Structures can only be unified with other variables or structures.
Two structures are unified by the same rules as (head, goal) pair when their names and number of components are equal furthermore these components should be unifiable pairwise by finding proper bindings.
Unification of lists follow the same rules as for structures.
An example
[X plus(1, X), times(2, X)] and [a, plus(1, Y), times(2, a)] is unified by X = a and Y = a.
Unification of sets is as follows;
An example
We have the fact pa({john|jane}, doe) which summarizes to pa(john, doe), pa(jane, doe).
The goal list is;
[ pa(X,doe) ?= pa({john|john},doe )],<<( "X",X)
and it yields two possible unification results;
[pa(john, doe) ?= pa({john|jane}, doe )],<<( "X",john)
[pa(jane, doe) ?= pa({john|jane}, doe )],<<( "X",jane)
We use the unify instruction since this multiplication might occur to different degrees for each term pairs in the head and first goal.
The idea is to perform the unification one term pair at a time rather than for the
entire(head goal) pair. and we have
[ pa(→X, doe) ?= pa(→{john|jane}, doe)],<<("X",X)
After which the term pair to be unified is marked with a preceding → into
[pa(john, →doe) ?= pa({john|jane}, →doe)],<<("X",john)
[pa(→X, doe) ?= pa({john|→jane}, doe)],<<("X",X)
Implementing a unification.
The following sets of C data types are used for the construction of terms.
struct variable{
char *name;
struct term *term;
}
struct structure{
char *functor;
int arity;
struct term **components;
}
typedef enum{Is_Constant, Is_Variable, Is_Structure} Term_Type;
typedef struct term{
Term_Type type;
union{
char *constant; //Is_Constant
struct variable variable; //Is_variable
struct structure structurel //Is_Structure
} term;
} Term;
We define Term as a discriminated union of constant, variable and structure.
A constant is represented as a pointer to its value and stored as a string.
A variable is also represented by a pointer and it's name is kept.
For bound variables, a pointer points to the term to which the variable is bound.
An unbound variable is marked by a null pointer.
A structure is implemented as a record with three fields specifying the functor, number of components and a pointer to an array of N components which is useful for allocation.
Unification of two terms
int unifyTerms(Term *goal_arg, Term *head_arg){
//Handle bound variables
Term *goal = deref(goal_arg);
Term *head = deref(head_arg);
if(goal->type == Is_Variable || head->type == Is_Variable){
return unify_unbound_variable(goal, head);
}else{
return unify_non_variables(goal, head);
}
}
Unification will distinguish the unification involving a variable and the unification involving two non-variable terms.
The above unify_terms() routine will take care of any bound variables by dereferencing the terms.
taking care of unbound variables
Term *deref(Term *t){
while(t->type == Is_Variable && t->term.variable.term != 0){
t = t->term.variable.term;
}
return t;
}
A term is unbound when it remains a variable after dereferencing.
The function deref() follows a pointer chain until it finds a non-variable or variable with a zero pointer.
Unification with at least one unbound variable.
int unify_unbound_variable(Term *goal, Term *head){
//handling identical values
if(goal == head)
//trivial unification of identical variables
else{
//bind unbound variable to the other term
if(head->type == Is_Variable){
trail_binding(head);
head->term.variable.term = goal;
}else{
trail_binding(goal);
goal->term.variable.term = head;
}
}
//unification succeeds
return 1;
}
The routine identifies a special case(where both bound and unbound variables are the same). This unification is trivial.
The term that is the variable is bound to the other term and this term is registered by the trail_binding function so that it can be unbound later during backtracking
Unifying two non-variables
int unify_non_variables(Term *goal, Term *head){
//handling differnt type terms
if(goal->type != head->type)
return 0;
switch(goal->type){
case Is_Constant: //both constants
return unify_constants(goal, head);
case Is_Structure:
return unify_structures(&goal->term.structure, &head->term.structure);
}
}
If two terms are of different types, then the unification fails otherwise a suited routine for the data type is called.
Unifying two constants
int unify_constants(Term *goal, Term *head){
return strcmp(goal->term.constant, head->term.constant) == 0;
}
Two constants are unified when a string comparison on their values succeed.
Unifying two structures
int unify_structures(struct structure *s_goal, struct structure *s_head){
int counter;
if(s_goal -> arity( !- s_head->arity || strcmp(s_goal->functor, s_head->arity; counter++){
if(!unify_terms(s_goal->components[counter[, s_head->components[counter]))
return 0;
}
return 1;
}
First the two structures are checked if they have the same arity and then unify_terms is called for each pair of terms.
If it succeeds, unification of the two structures succeeds otherwise it fails.
Unifying two unbound variables.
Variables are associated with each other such that they are both unbound, when one of them is bound to a constant or third variable, so will the other.
This is done by binding one of the variables to the other and dereferencing any variable before use so as to find out what it is actually bound to.
The problem is that binding an unbound variable B to an unbound variable A results in an unbound variable B.
The image shows the expected result of a sequence of four variable-variable bindings, first B-A, C-B, D-B and E-C.
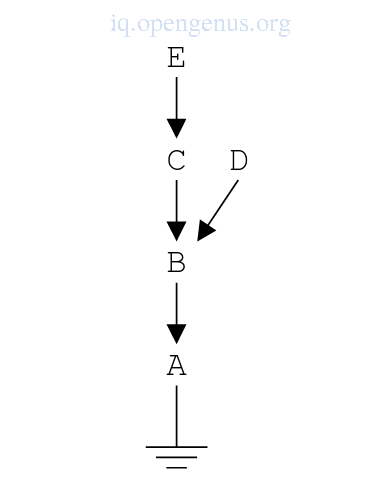
The image shows the actual binding.
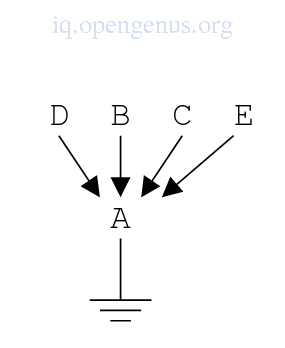
Binding B-A results in a binding B-A but binding C-B starts by dereferencing B and C only to find B is actually A therefore in the implementation C is bound to A instead of B. This happens for bindings D-B and E-C.
Summary.
In logic programming the user specifies the problem statements and the logic programming system will find the solution to the problem by tracing through the given information.
Prolog is most widely used logic programming language, it involves a pattern-matching mechanism, a backtracking strategy which searches for possible solutions and uniform data structures from which programs are built.
References.
- Logic and Prolog : Richard Spencer-Smith.
- Logic programming courseware by California State University, Sacramento.
- Modern Compiler Design 2nd edition Dick Grune Kees van Reeuwijk Henri E. Bal Ceriel J.H. Jacobs Koen Langendoen.
