
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored 3 approaches to merge K sorted arrays such that the resulting array is sorted as well. This involve the concept of Min / Max Heap.
Table of contents:
- Problem Statement
- Approach 1 : Naive Approach
- Approach 2: Using merging
- Approach 3: Using Min-Heap
Pre-requisite: Min/ Max Heap
Problem Statement
Given K no. of sorted arrays of size N each, merge and sort them, print the sorted output.
Example
Input:
3 4
1 4 7 10
2 5 8 11
3 6 9 12
Output:
1 2 3 4 5 6 7 8 9 10 11 12
Solution
Approach 1 : Naive Approach
The basic idea behind this approach is to iterate through each array and keep track of the current element in each array, then add the smallest element to the final result array. This process is repeated until all elements have been added to the final result array.
This process is as follows:
- First, initialize a array of size N * K.
- Then, for each array in the input, we create a pointer to keep track of the current element in that array.
- We then iterate through each array and compare the current element at the pointer for each array.
- The smallest element is added to the final result array, and the pointer for the array with the smallest element is incremented.
This process is repeated until all elements have been added to the final result array.
Implementation
Implementation of naive approach in java:
public class Main {
public static int[] merge(int[][] arrays) {
int k = arrays.length;
int n = arrays[0].length;
// Initialize the result array
int[] result = new int[k * n];
// Create an array to keep track of the current element for each input array
int[] pointer = new int[k];
// Initialize the result array index
int index = 0;
// Repeat until all elements have been added to the final result array
while (index < k * n) {
int min = Integer.MAX_VALUE;
int minArray = -1;
// Find the array with the smallest current element
for (int i = 0; i < k; i++) {
if (pointer[i] < n && arrays[i][pointer[i]] < min) {
min = arrays[i][pointer[i]];
minArray = i;
}
}
// Add the smallest element to the final result array
result[index++] = min;
pointer[minArray]++;
}
return result;
}
public static void main(String[] args) {
int K = s.nextInt();
int N = s.nextInt();
int arr[][] = new int[k][n];
for(int i=0,; i<k; i++) {
for(int j=0; j<n; j++) {
arr[i][j] = s.nextInt();
}
}
int[] result = merge(arr);
for (int i : result) {
System.out.print(i + " ");
}
}
}
- Below Image shows the representation of naive approach
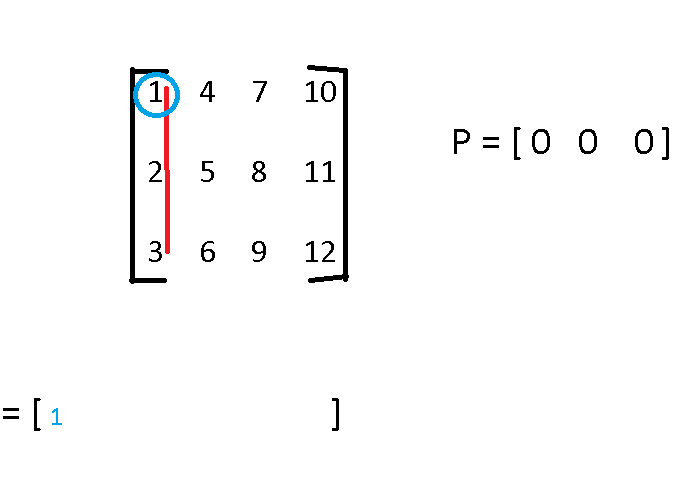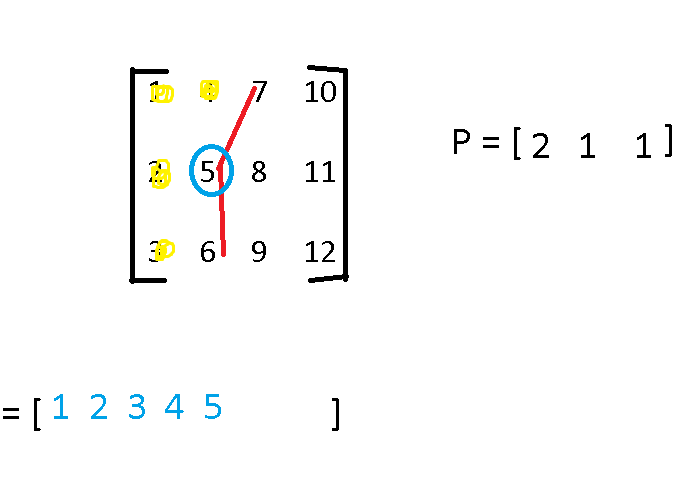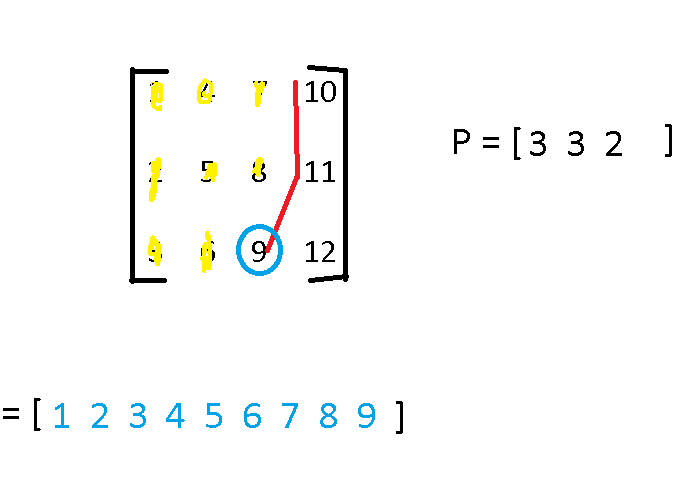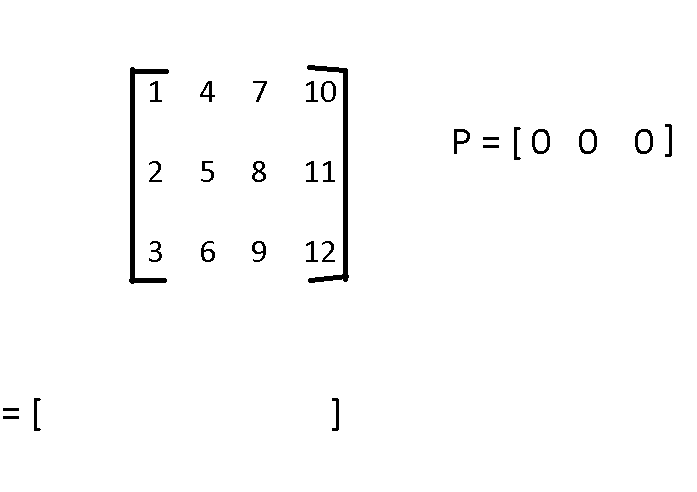
Step by Step Guide to use naive approach
- Initialize an empty array called result to store the final merged and sorted array.
- Create an array called pointers of size K to keep track of the current index of each input array. Initialize each element to 0.
- Create a variable size to store the total number of elements in all the input arrays.
- Create a while loop that continues until size is equal to the number of elements added to the final result array.
- Inside the while loop, initialize a variable min to a very large value (e.g. Integer.MAX_VALUE) and a variable minArray to -1.
- Use a for loop to iterate through each input array. In each iteration, check if the current pointer index is less than N and if the current element in the array is less than min.
- If the current element is smaller than min, update min to the current element and minArray to the current array index.
- After the for loop, add the value of min to the result array and increment the pointer index of the array at index minArray by 1.
- Also, increment the size variable by 1.
- Repeat steps 4 to 9 until size is equal to the total number of elements in all input arrays.
- Return the result array.
Complexity Analysis
Time complexity: O(N * K^2)
- In each iteration, we also compare the current element at the pointer for each array, which take O(K) time.
- So the overall time complexity becomes O(K * N * K).
Space Complexity: O(N * K)
- we are using an additional array of size O(N * K) to store the final result.
Approach 2: Using merging
The basic idea behind this approach is to repeatedly merge pairs of arrays until we are left with a single merged and sorted array.
This process is as follows:
- The first step is to divide the K arrays into pairs and merge each pair using a merge sort-like approach.
- We can then take the resulting arrays and merge them again, continuing this process until we have a single merged and sorted array.
One key advantage of this approach is that it can be easily parallelized, allowing us to take advantage of multiple processors or threads to speed up the merge process.
Implementation
Implementation of merging approach in java:
public class Main {
public static int[] merge(int[][] arrays) {
int k = arrays.length;
int n = arrays[0].length;
// Initialize the result array
int[] result = new int[k * n];
// Repeat until we have a single merged array
while (k > 1) {
int index = 0;
for (int i = 0; i < k; i += 2) {
int[] left = arrays[i];
int[] right = i + 1 < k ? arrays[i + 1] : new int[0];
arrays[index++] = mergeTwoArrays(left, right);
}
k = (k + 1) / 2;
}
return arrays[0];
}
// Helper method to merge two sorted arrays
public static int[] mergeTwoArrays(int[] left, int[] right) {
int[] result = new int[left.length + right.length];
int i = 0, j = 0, k = 0;
while (i < left.length && j < right.length) {
if (left[i] < right[j]) {
result[k++] = left[i++];
} else {
result[k++] = right[j++];
}
}
while (i < left.length) {
result[k++] = left[i++];
}
while (j < right.length) {
result[k++] = right[j++];
}
return result;
}
public static void main(String[] args) {
int K = s.nextInt();
int N = s.nextInt();
int arr[][] = new int[k][n];
for(int i=0,; i<k; i++) {
for(int j=0; j<n; j++) {
arr[i][j] = s.nextInt();
}
}
int[] result = merge(arr);
for (int i : result) {
System.out.print(i + " ");
}
}
}
- Below Image shows the representation of merging approach

Complexity Analysis
Time Complexity: O(N * K * log(K))
- The time complexity of this algorithm is O(N * K * log(K)), where N is the size of each array and K is the number of arrays.
Space Complexity: O(N * K) - we are using an additional array of size O(N * K) to store the final result.
Approach 3: Using Min-Heap
The basic idea behind using a min heap is that we can insert the first element from each of the K arrays into the heap and then repeatedly extract the minimum element from the heap and add it to the final sorted array. After extracting an element from the heap, we then insert the next element from the same array into the heap, ensuring that the heap always contains the smallest element from each of the K arrays.
This process is as follows:
- First we create a min heap with a size of K and insert the first element from each of the K arrays into the heap.
- We then repeatedly extract the minimum element from the heap and add it to the final sorted array.
- After extracting an element from the heap, we then insert the next element from the same array into the heap, ensuring that the heap always contains the smallest element from each of the K arrays.
Implementation
Implementation of Min-heap approach in java:
import java.util.PriorityQueue;
public class Main {
public static int[] merge(int[][] arrays) {
// Create a min heap with a size of K
PriorityQueue<ArrayContainer> heap = new PriorityQueue<ArrayContainer>(arrays.length, (a, b) -> a.array[a.index] - b.array[b.index]);
// Insert the first element from each of the K arrays into the heap
for (int i = 0; i < arrays.length; i++) {
heap.offer(new ArrayContainer(arrays[i], 0));
}
// Create a final array to store the merged elements
int[] result = new int[arrays.length * arrays[0].length];
int index = 0;
// Repeat until the heap is empty
while (!heap.isEmpty()) {
// Extract the minimum element from the heap and add it to the final array
ArrayContainer ac = heap.poll();
result[index++] = ac.array[ac.index];
// Insert the next element from the same array into the heap
if (ac.index < ac.array.length - 1) {
heap.offer(new ArrayContainer(ac.array, ac.index + 1));
}
}
return result;
}
// Helper class to store array and current index
static class ArrayContainer {
int[] array;
int index;
ArrayContainer(int[] array, int index) {
this.array = array;
this.index = index;
}
}
public static void main(String[] args) {
int K = s.nextInt();
int N = s.nextInt();
int arr[][] = new int[k][n];
for(int i=0,; i<k; i++) {
for(int j=0; j<n; j++) {
arr[i][j] = s.nextInt();
}
}
int[] result = merge(arr);
for (int i : result) {
System.out.print(i + " ");
}
}
}
- Below Image shows the representation of min-heap approach
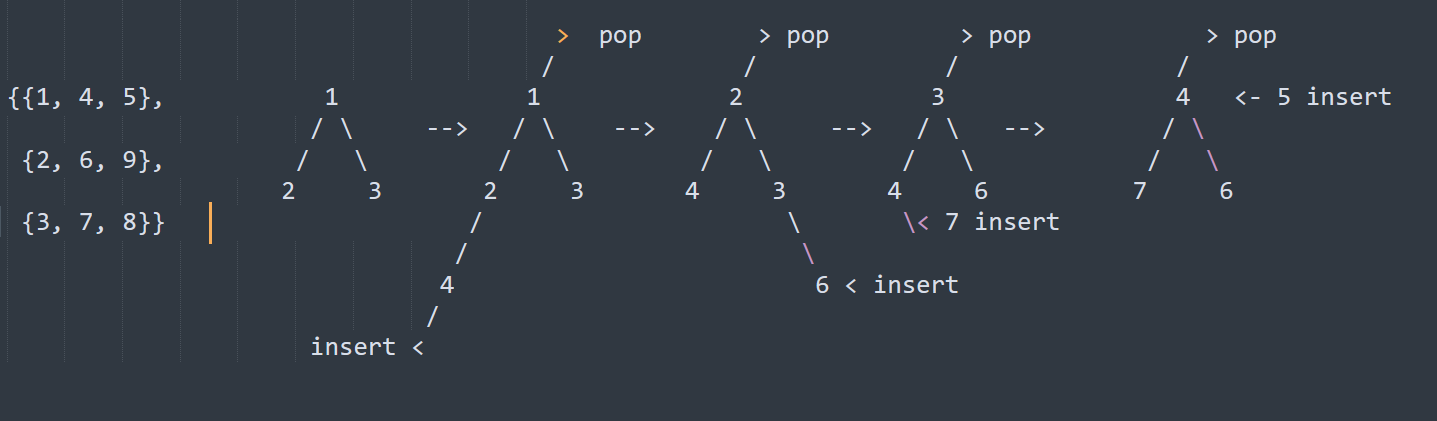
and so on.
Explanation
- In this example, the merge() method takes in a 2D array of integers called arrays and returns the merged and sorted array.
- The ArrayContainer class is a helper class which is used to store the array and current index. This is used to extract the next element from the same array after the current element has been extracted from the heap.
Step by Step Guide to use min-heap approach
- Initialize an empty array called result to store the final merged and sorted array.
- Create a min-heap of size K to store the current element of each input array.
- Use a for loop to iterate through each input array and add the first element of each array to the min-heap.
- Create a while loop that continues until the min-heap is empty.
5 Inside the while loop, remove the minimum element from the min-heap and add it to the result array. - Check if the input array from which the minimum element was removed has any more elements. If it does, add the next element to the min-heap.
- Repeat steps 4-6 until the min-heap is empty.
- Return the result array
Complexity Analysis
Time Complexity: O(N * K * log(K)),
- where N is the size of each array and K is the number of arrays.
Space Complexity: O(K)
- as we only need to store the elements in the heap at any given time. or O(N * K) if we want to store it in a output array.
With this article at OpenGenus, you must have the complete idea of solving this problem of merging K sorted arrays.
