
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 45 minutes
Heap is a binary tree with two special properties: it must have all its nodes in specific order and its shape must be complete.
Keep in mind-
- We can have duplicate values in a heap — there’s no restriction against that.
- A heap doesn’t follow the rules of a binary search tree; unlike binary search trees, the left node does not have to be smaller than the right node! The ordering of the child nodes isn’t important for a heap; the only ordering that matters is the heap-order property, or the ordering of parent nodes compared to their children.
Heap can be broadly classified in two types :
1. Min heap
2. Max heap
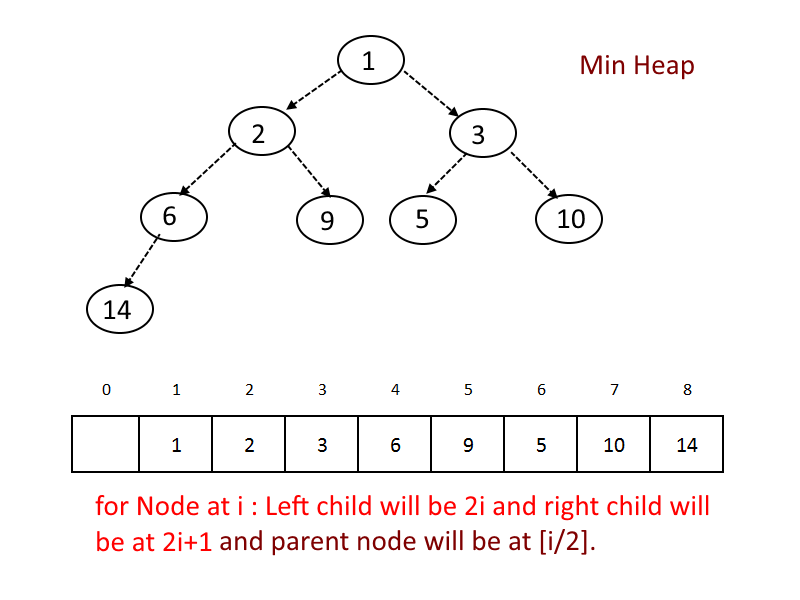
Min Heap
A min heap is a heap where every single parent node, including the root, is less than or equal to the value of its children nodes.
The most important property of a min heap is that the node with the smallest, or minimum value, will always be the root node.
Max Heap
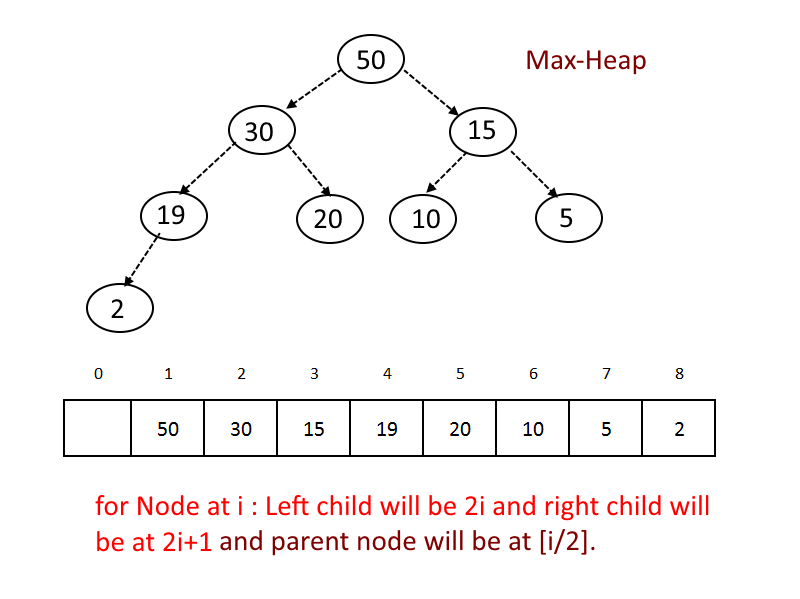
A max heap is effectively the converse of a min heap; in this format, every parent node, including the root, is greater than or equal to the value of its children nodes.
The important property of a max heap is that the node with the largest, or maximum value will always be at the root node.
Implementation
- Use array to store the data.
- Start storing from index 1, not 0.
- For any given node at position i:
- Its Left Child is at [2*i] if available.
- Its right child is at [2*i+1] if available.
- Its Parent Node is at [i/2] if available.
Heap Majorly has 3 operations –
- Insert Operation(Time complexity O(log n))
- Delete Operation (Time complexity O(log n))
- Extract-Min (OR Extract-Max) (Time complexity O(n))
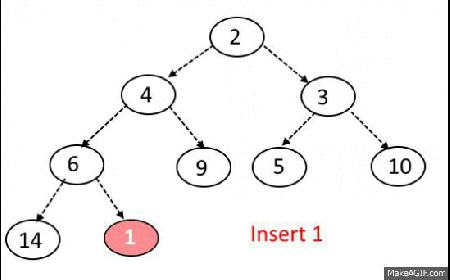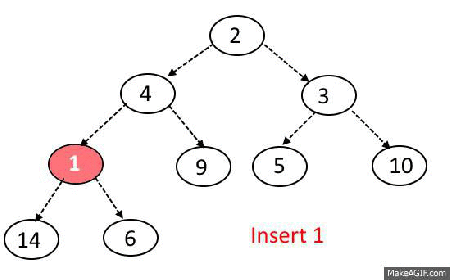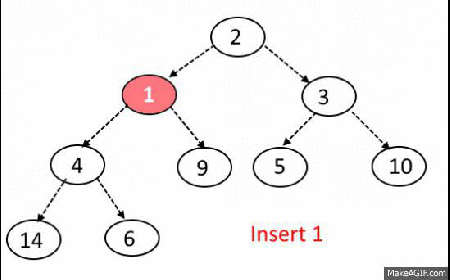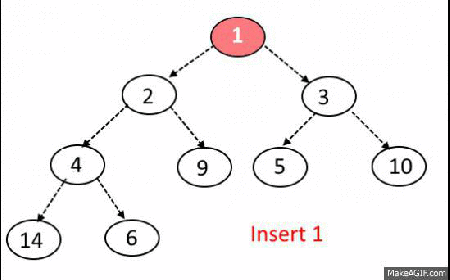
Insert Operation
Steps:
- Add the element at the bottom leaf of the Heap.
- Perform the Bubble-Up operation.
- All Insert Operations must perform the bubble-up operation(it is also called as up-heap, percolate-up, sift-up, trickle-up, heapify-up, or cascade-up)
Psuedocode
MIN-HEAP-INSERT(A,key)
heap-size[A] <- heap-size[A] + 1
A[heap-size[A]] <- +inf
HEAP-DECREASE-KEY(A,heap-size[A],key)
Bubble-up Operation
Steps:
- If inserted element is smaller than its parent node in case of Min-Heap OR greater than its parent node in case of Max-Heap, swap the element with its parent.
- Keep repeating the above step, if node reaches its correct position, STOP.
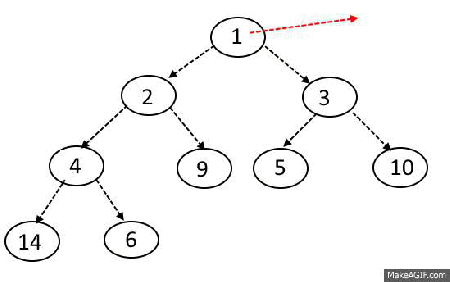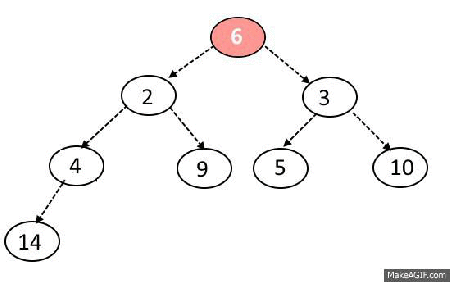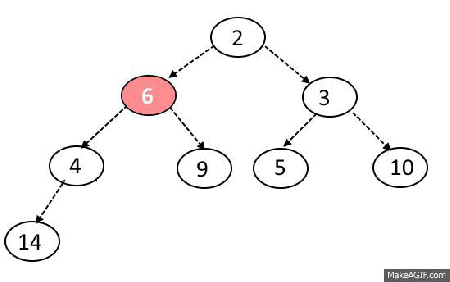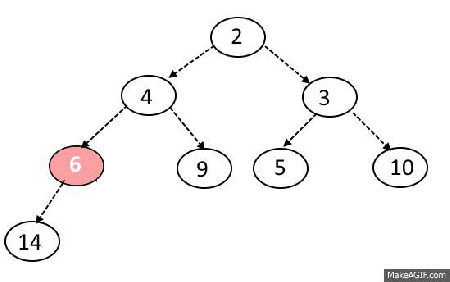
Extract-Min OR Extract-Max Operation
Steps:
- Take out the element from the root.( it will be minimum in case of Min-Heap and maximum in case of Max-Heap).
- Take out the last element from the last level from the heap and replace the root with the element.
- Perform Sink-Down.
- All delete operation must perform Sink-Down Operation ( also known as bubble-down, percolate-down, sift-down, trickle down, heapify-down, cascade-down).
Psuedocode:
HEAP-EXTRACT-MIN(A)
if heap-size[A] < 1
then error ‘‘heap underflow’’
min <- A[1]
A[1] <- A[heap-size[A]]
heap-size[A] <- heap-size[A] - 1
MIN-HEAPIFY(A,1)
return min
Sink-Down Operation
Steps:
- If replaced element is greater than any of its child node in case of Min-Heap OR smaller than any if its child node in case of Max-Heap, swap the element with its smallest child(Min-Heap) or with its greatest child(Max-Heap).
- Keep repeating the above step, if node reaches its correct position, STOP.
Psuedocode:
HEAP-DECREASE-KEY(A,i,key)
if key > A[i]
then error ‘‘new key is larger than current key’’
A[i] <- key
while i > 1 and A[parent(i)] > A[i]
do exchange A[i] <-> A[parent(i)]
i <- parent(i)
Delete Operation
Steps:
- Find the index for the element to be deleted.
- Take out the last element from the last level from the heap and replace the index with this element .
- Perform Sink-Down.
Complete implementation of Min-heap in Java
public class minHeap {
public int capacity;
public int [] mH;
public int currentSize;
public minHeap(int capacity){
this.capacity=capacity;
mH = new int [capacity+1];
currentSize =0;
}
public void createHeap(int [] arrA){
if(arrA.length>0){
for(int i=0;i<arrA.length;i++){
insert(arrA[i]);
}
}
}
public void display(){
for(int i=1;i<mH.length;i++){
System.out.print(" " + mH[i]);
}
System.out.println("");
}
public void insert(int x) {
if(currentSize==capacity){
System.out.println("heap is full");
return;
}
currentSize++;
int idx = currentSize;
mH[idx] = x;
bubbleUp(idx);
}
public void bubbleUp(int pos) {
int parentIdx = pos/2;
int currentIdx = pos;
while (currentIdx > 0 && mH[parentIdx] > mH[currentIdx]) {
swap(currentIdx,parentIdx);
currentIdx = parentIdx;
parentIdx = parentIdx/2;
}
}
public int extractMin() {
int min = mH[1];
mH[1] = mH[currentSize];
mH[currentSize] = 0;
sinkDown(1);
currentSize--;
return min;
}
public void sinkDown(int k) {
int smallest = k;
int leftChildIdx = 2 * k;
int rightChildIdx = 2 * k+1;
if (leftChildIdx < heapSize() && mH[smallest] > mH[leftChildIdx]) {
smallest = leftChildIdx;
}
if (rightChildIdx < heapSize() && mH[smallest] > mH[rightChildIdx]) {
smallest = rightChildIdx;
}
if (smallest != k) {
swap(k, smallest);
sinkDown(smallest);
}
}
public void swap(int a, int b) {
int temp = mH[a];
mH[a] = mH[b];
mH[b] = temp;
}
public boolean isEmpty() {
return currentSize == 0;
}
public int heapSize(){
return currentSize;
}
public static void main(String args[]){
int arrA [] = {3,2,1,7,8,4,10,16,12};
System.out.print("Original Array : ");
for(int i=0;i<arrA.length;i++){
System.out.print(" " + arrA[i]);
}
minHeap m = new minHeap(arrA.length);
System.out.print("\nMin-Heap : ");
m.createHeap(arrA);
m.display();
System.out.print("Extract Min :");
for(int i=0;i<arrA.length;i++){
System.out.print(" " + m.extractMin());
}
}
}
Output
Original Array : 3 2 1 7 8 4 10 16 12
Min-Heap : 1 3 2 7 8 4 10 16 12
Extract Min : 1 2 3 4 7 8 10 12 16
Complete implementation of Max-heap in Java
public class maxHeap {
public int capacity;
public int [] mH;
public int currentSize;
public maxHeap(int capacity){
this.capacity=capacity;
mH = new int [capacity+1];
currentSize =0;
}
public void createHeap(int [] arrA){
if(arrA.length>0){
for(int i=0;i<arrA.length;i++){
insert(arrA[i]);
}
}
}
public void display(){
for(int i=1;i<mH.length;i++){
System.out.print(" " + mH[i]);
}
System.out.println("");
}
public void insert(int x) {
if(currentSize==capacity){
System.out.println("heap is full");
return;
}
currentSize++;
int idx = currentSize;
mH[idx] = x;
bubbleUp(idx);
}
public void bubbleUp(int pos) {
int parentIdx = pos/2;
int currentIdx = pos;
while (currentIdx > 0 && mH[parentIdx] < mH[currentIdx]) {
swap(currentIdx,parentIdx);
currentIdx = parentIdx;
parentIdx = parentIdx/2;
}
}
public int extractMax() {
int max = mH[1];
mH[1] = mH[currentSize];
mH[currentSize] = 0;
sinkDown(1);
currentSize--;
return max;
}
public void sinkDown(int k) {
int greatest = k;
int leftChildIdx = 2 * k;
int rightChildIdx = 2 * k+1;
if (leftChildIdx < heapSize() && mH[greatest] < mH[leftChildIdx]) {
greatest = leftChildIdx;
}
if (rightChildIdx < heapSize() && mH[greatest] < mH[rightChildIdx]) {
greatest = rightChildIdx;
}
if (greatest != k) {
swap(k, greatest);
sinkDown(greatest);
}
}
public void swap(int a, int b) {
int temp = mH[a];
mH[a] = mH[b];
mH[b] = temp;
}
public boolean isEmpty() {
return currentSize == 0;
}
public int heapSize(){
return currentSize;
}
public static void main(String args[]){
int arrA [] = {3,2,1,7,8,4,10,16,12};
System.out.print("Original Array : ");
for(int i=0;i<arrA.length;i++){
System.out.print(" " + arrA[i]);
}
maxHeap m = new maxHeap(arrA.length);
System.out.print("\nMax-Heap : ");
m.createHeap(arrA);
m.display();
System.out.print("Extract Max :");
for(int i=0;i<arrA.length;i++){
System.out.print(" " + m.extractMax());
}
}
}
Output
Original Array : 3 2 1 7 8 4 10 16 12
Max-Heap : 12 10 7 8 2 1 4 0 3
Extract Max : 12 10 8 7 4 3 2 1 0
Applications
The heap data structure has many applications:
- Heapsort: One of the best sorting methods being in-place and with no quadratic worst-case scenarios.
- Selection algorithms: A heap allows access to the min or max element in constant time, and other selections (such as median or kth-element) can be done in sub-linear time on data that is in a heap.
- Graph algorithms: By using heaps as internal traversal data structures, run time will be reduced by polynomial order. Examples of such problems are Prim's minimal-spanning-tree algorithm and Dijkstra's shortest-path algorithm.
- Priority Queue: A priority queue is an abstract concept like "a list" or "a map"; just as a list can be implemented with a linked list or an array, a priority queue can be implemented with a heap or a variety of other methods.
- K-way merge: A heap data structure is useful to merge many already-sorted input streams into a single sorted output stream. Examples of the need for merging include external sorting and streaming results from distributed data such as a log structured merge tree. The inner loop is obtaining the min element, replacing with the next element for the corresponding input stream, then doing a sift-down heap operation. (Alternatively the replace function.) (Using extract-max and insert functions of a priority queue are much less efficient.)
- Order statistics: The Heap data structure can be used to efficiently find the kth smallest (or largest) element in an array.
