
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes
When building a deep learning project the most common problem we all face is choosing the correct hyperparameters (often known as optimizers). This is critical as the hyperparameters determine the expertise of the machine learning model.
In Machine Learning (ML hereafter), a hyperparameter is a configuration variable that’s external to the model and whose value is not estimated from the data given. Hyperparameters are an essential part of the process of estimating model parameters and are often defined by the practitioner.
When an ML algorithm is used for a specific problem, for example when we are using a grid search or a random search algorithm, then we are actually tuning the hyperparameters of the model to discover the values that help us to achieve the most accurate predictions.
What is Learning Rate?
Learning rate (λ) is one such hyperparameter that defines the adjustment in the weights of our network with respect to the loss gradient descent. It determines how fast or slow we will move towards the optimal weights
The Gradient Descent Algorithm estimates the weights of the model in many iterations by minimizing a cost function at every step.
Here is the algorithm:
Repeat until convergence {
Wj = Wj - λ θF(Wj)/θWj
}
Where:
- Wj is the weight
- θ is the theta
- F(Wj) is the cost function respectively.
In order for Gradient Descent to work, we must set the learning rate to an appropriate value. This parameter determines how fast or slow we will move towards the optimal weights. If the learning rate is very large we will skip the optimal solution. If it is too small we will need too many iterations to converge to the best values. So using a good learning rate is crucial.
In simple language, we can define learning rate as how quickly our network abandons the concepts it has learned up until now for new ones.
Learning rate explained through a child's interaction
To understand this better let's consider an example.
If a child sees ten dogs and all of them are black in color, he might believe that all dogs are black and would consider this as a feature when trying to identify a dog.
Imagine he’s shown a white dog, and his parents tell him that it’s a dog. With a desirable learning rate, he would quickly understand that black color is not an important feature of dogs and would look for another feature.
But with a low learning rate, he would consider the white dog as an outlier and would continue to believe that all dogs are black.
And if the learning rate is too high, he would instantly start to believe that all dogs are white even though he has seen more black dogs than white ones.
The point is it's’ really important to achieve a desirable learning rate because:
- both low and high learning rates results in wasted time and resources
- A lower learning rate means more training time
- more time results in increased cloud GPU costs
- a higher rate could result in a model that might not be able to predict anything accurately
A desirable learning rate is one that’s low enough so that the network converges to something useful but high enough so that it can be trained in a reasonable amount of time.
Tuning the learning rate
The learning rate is the most important hyperparameter for tuning neural networks. A good learning rate could be the difference between a model that doesn’t learn anything and a model that presents state-of-the-art results.
The below diagram demonstrates the different scenarios one can fall into when configuring the learning rate.
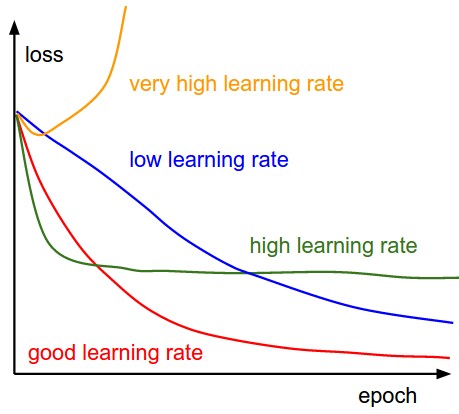
Effect of various learning rates on convergence (Img Credit: cs231n)
The obvious way to find a desirable or optimal learning rate is through trial and error. To do this efficiently, there are a few ways that we should adhere to.
Search from coarse to fine learning rate
A learning rate of 0.01 and 0.011 are unlikely to yield vastly different results. Even if they did, searching in such small increments is very costly and inefficient: what if both learning rates caused the model to diverge? The time spent training would be a waste.
A more efficient way is to try widely different learning rates to determine the range of learning rates you should explore and concentrate your efforts there.
For instance, whenever I am trying to tune the learning rate, I generally start off by searching across the learning rates 1e-7, 1e-6, 1e-5, … 0.01, 0.1, 1. In other words, I search across various orders of 10 to find an optimal range of learning rates. Then, I search in smaller increments. For instance, if I found the optimal range to be somewhere between 0.01 and 0.1, I would then start searching learning rates in that range such as 0.03. This is exactly similar to the idea behind binary search and is a widely applicable technique.
Don’t start off by training on the entire dataset
Starting off with the entire dataset is likely to be a waste of time. Chances are, some learning rates will cause your loss to diverge or fluctuate and some learning rates are likely to train very slowly, so these orders of learning rates can be removed from your search after a few iterations.
Although trial and error is a relatively fail-proof way of tuning the learning rate, a more efficient way which does minimal training to find the best learning rate to start from is “Learning Rate Test”.
The basic idea is that you want to efficiently find the maximum learning rate you can use which will improve the loss. In order to find that value, you train slightly with multiple learning rates and see how the loss changes.
The actual procedure is:
Choose a minimum and maximum learning rate to search through (e.g. 1e-7 and 0.1)
Train the model for several epochs using SGD while linearly increasing the learning rate from the minimum to maximum learning rate.
At each iteration, record the accuracy (or loss).
Plot the test accuracy, and see where the loss/accuracy starts to improve, and when it starts to get worse/plateau/to become ragged. The latter learning rate is the maximum learning rate that converges and is a good value for your initial learning rate. The former learning rate, or 1/3 – 1/4 of the maximum learning rates is a good minimum learning rate that you can decrease if you are using learning rate decay.
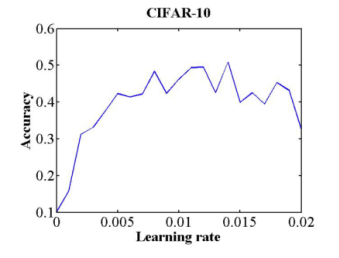
If the test accuracy curve looks like the above diagram, a good learning rate to begin from would be 0.006, where the loss starts to become jagged.
Learning rate should be adaptive
This method of improving the convergence rate of hyperparameters reduces the need for the manual tuning of the initial learning rate. This method works by dynamically updating the learning rate during optimization using the gradient with respect to the learning rate of the update rule itself. Computing this "hypergradient" needs little additional computation, requires only one extra copy of the original gradient to be stored in memory, and relies upon nothing more than what is provided by reverse-mode automatic differentiation.
Conclusion and further reading
It’s clear that configuring a model’s learning rate is a crucial task, and whatever approach you opt for, it will be time-consuming and challenging.
A powerful technique that involves selecting a range of learning rates for a neural network has been discussed in the paper “Cyclical Learning Rates for Training Neural Networks" by Leslie N. Smith.
