Reading time: 30 minutes

A vertex cover of a graph G is a set of vertices, V_c, such that every edge in G has at least one of vertex in V_c as an endpoint. This means that every vertex in the graph is touching at least one edge.

Minimum vertex cover
The vertex covering number also called the minimum vertex covering number is the size of the smallest vertex cover of G and is denoted τ(G).

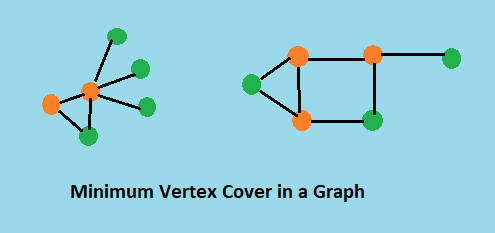
The problem of finding a minimum vertex cover is a classical optimization problem in computer science and is an NP-hard problem. In fact, the vertex cover problem was one of Karp's 21 NP-complete problems and is therefore a classical NP-complete problem in complexity theory.

Vertex Cover Problem is a known NP Complete problem, i.e., there is no polynomial time solution for the graph problem. There are approximate polynomial time algorithms to solve the graph problem though which gives the aproximation of the answer not greater than twice of minimum vertex cover.
Although the problem is NP complete, it can be solved in polynomial time for following types of graphs.

1. Bipartite Graph
2. Tree

Here we will see Naive approach and Dynamic programming approach to solve the vertex cover problem for a binary tree graph and reduce the complexity from O(2ⁿ) to O(n²).

1. Naive Approach

The idea of the approach to find minimum vertex covr in a tree is to consider following two possibilities for root and recursively for all the nodes down the root.

1) Root is a part of vertex cover:
In this case root covers all children edges. We recursively calculate size of vertex covers for left and right subtrees and add 1 to the result (for root).
2) Root is not a part of vertex cover:
In this case, both children of root must be included in vertex cover to cover all root to children edges. We recursively calculate size of vertex covers of all grandchildren and number of children to the result (for two children of root).

Finaly we take the minimum of the two, and return the result.

// The function returns size of the minimum vertex cover 
int vertexCover(struct node *root) 
{
	// The size of minimum vertex cover is zero if tree is empty or there is only one node i.e. root.
	if (root == NULL) 
		return 0; 
	if (root->left == NULL && root->right == NULL) 
		return 0; 

	// Calculate size of vertex cover when root is a part of it.
	int size_root_inc = 1 + vertexCover(root->left) + vertexCover(root->right); 

	// Calculate size of vertex cover when root is not a part of it. 
	int size_root_exc = 0; 
	if (root->left) 
	size_root_exc += 1 + vertexCover(root->left->left) + vertexCover(root->left->right); 
	if (root->right) 
	size_root_exc += 1 + vertexCover(root->right->left) + vertexCover(root->right->right); 

	// Return the minimum of the two
	return min(size_root_inc, size_root_exc); 
}

The complexity of this approach is exponential i.e. O(2ⁿ) because we recursively solve the same subproblems many times.

2. Dynamic Programmic Approach

The problem has overlapping subprolems property. Like typical Dynamic Programming(DP) problems, re-computations of same subproblems can be avoided by storing the solutions to subproblems and solving problems in bottom up manner.
We do the same for this problem, we solve the vertex cover problem in bottom up manner and store the solutions of the subproblems to calculate the minimum vertex cover of the problem.

So here we use the same approach as the naive one but with memoization. We a special value vc to each node i.e. we store the minimum vertex cover to each node of the tree which represents the minimum vertex cover of the partial tree rooted at that node.
In bottom up manner we start from the leaf nodes, compute its minimum vertex cover and store it to that node. Now for the parent node we recursively compute the vertex cover from its children nodes and store it to that node. In this approach we calculate the vertex cover of any node only once and reuse the stored value if required.

// A dynamic programmic based solution that returns size of the minimum vertex cover.
int vertexCover(struct node *root) 
{
	// The size of minimum vertex cover is zero if tree is empty or there is only one node i.e. root.
	if (root == NULL)
		return 0; 
	if (root->left == NULL && root->right == NULL)
		return 0; 

	// If vertex cover for this node is already evaluated, then return it 
	// to save recomputation of same subproblem again. 
	if (root->vc != -1)
		return root->vc;

	// Calculate size of vertex cover when root is part of it 
	int size_root_inc = 1 + vertexCover(root->left) + vertexCover(root->right);

	// Calculate size of vertex cover when root is not part of it
	int size_root_exc = 0;
	if (root->left)
	size_root_exc += 1 + vertexCover(root->left->left) + vertexCover(root->left->right); 
	if (root->right) 
	size_root_exc += 1 + vertexCover(root->right->left) + vertexCover(root->right->right); 

	// Minimum of two values is vertex cover, store it before returning.
	root->vc = min(size_root_inc, size_root_exc); 

    // returning minimum of the two.
	return root->vc; 
} 

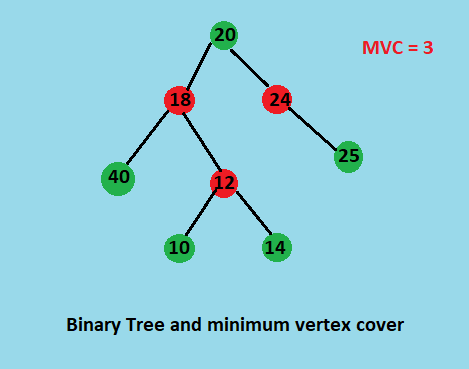
The DP approach evalutes vertex cover for each node exactly once and reconstructs the solution for parent node from the solution of its children nodes,and in similar way computes the minimum vertex cover for the root node.

Implementation

Code in C++

/* Dynamic programming based solution for Vertex Cover problem for a Binary Tree */
#include <iostream>
#include <cstdlib>

int min(int x, int y) { return (x < y) ? x : y; }

/* A binary tree node has data, pointer to left child and a pointer to 
right child */
struct node
{
    int data;
    int vc;
    struct node *left, *right;
    node(int data) : data(data),vc(-1),left(NULL),right(NULL){}
};
// A dynamic programmic based solution that returns size of the minimum vertex cover.
int vertexCover(struct node *root)
{
    // The size of minimum vertex cover is zero if tree is empty or there is only one node i.e. root.
    if (root == NULL)
        return 0;
    if (root->left == NULL && root->right == NULL)
        return 0;

    // If vertex cover for this node is already evaluated, then return it.
    // to save recomputation of same subproblem again.
    if (root->vc != -1)
        return root->vc;

    // Calculate size of vertex cover when root is part of it
    int size_root_inc = 1 + vertexCover(root->left) + vertexCover(root->right);

    // Calculate size of vertex cover when root is not part of it
    int size_root_exc = 0;
    if (root->left)
        size_root_exc += 1 + vertexCover(root->left->left) + vertexCover(root->left->right);
    if (root->right)
        size_root_exc += 1 + vertexCover(root->right->left) + vertexCover(root->right->right);

    // Minimum of two values is vertex cover, store it before returning.
    root->vc = min(size_root_inc, size_root_exc);

    // returning minimum of the two.
    return root->vc;
}

struct node *newNode(int data)
{
    struct node *temp = new node(data);
    return temp;
};

int main()
{
    struct node *root = newNode(20);
    root->left = newNode(18);
    root->left->left = newNode(40);
    root->left->right = newNode(12);
    root->left->right->left = newNode(10);
    root->left->right->right = newNode(14);
    root->right = newNode(24);
    root->right->right = newNode(25);

    std::cout << "Size of the minimum vertex cover is " << vertexCover(root);
    return 0;
}

Output

Size of the minimum vertex cover is 3

Complexity

Time Complexity

• The naive approach takes O(2ⁿ) time in the worst case.
• The dynamic programming approach takes O(n²) in the worst case and Θ(3*n) in average case.

Space Complexity

• The naive approach takes O(1) auxiliary space.
• The DP approach takes O(1) auxiliary space.

Applications

• The Traveling Salesperson Problem
  The traveling salesperson problem is a classic computer science problem discussed in graph theory and complexity theory.
• Efficient dynamic detection of race conditions.