We are given a string with repeating characters and we need to rearrange this string such that no two adjacent characters are same. To solve this problem, we will use Priority Queue data structure and will be able to rearrange the string in O(N logN) time where N is the number of characters in the string.

Examples

Input String: aabc
Output String: acba

Input String: aaabcab
Output String: abacaba

Input String: aabbc
Output String: aback

Input String: aaab
Output String: NOT POSSIBLE

Input String: aa
Output String: NOT POSSIBLE

Solution

We will use a priority queue to store the characters with their frequencies and then pick the character with the highest frequency and add it to the output string.

Now we will add the character again in the queue if its frequency is more than 1. We will repeat this procedure until the queue is empty. If at the end the length of output string is same as the length of the input string then output the string else output 'Not Possible'.

Algorithm

1. Build a priority queue that will store all the characters with their frequencies.
2. Create a variable ‘prev' that will store the previously added character and initialize it with ‘#' character and -1 frequency.
3. While our queue is not empty.
   1. Remove an element from the queue and add it to the output string.
   2. Decrement the frequency of this element by 1.
   3. Add this element back to the queue if its frequency is > 0.
   4. Set 'prev' variable to this element.
4. If the length of output string is equal to the input string output the result else output ’Not possible'.

Explanation

Let the input string be "aabc".

Now we will add the characters in the queue, and one by repeat the step 3rd in the algorithm until our queue is not empty.

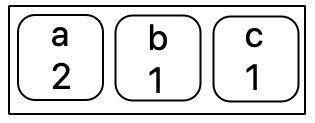
As you can see we have all three characters in the queue and we will remove one element from the head of the queue and add it to the output string.
Output String = "a".

After removing the character we have again added it to the queue as it's frequency was > 0.

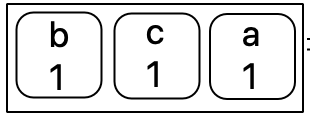
Again we will remove an element from the queue and add it to our string.
Output String = "ab".

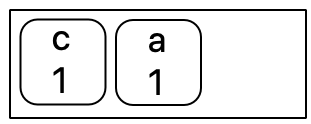
Output String = "abc".

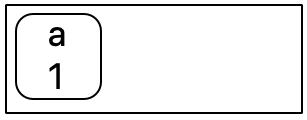
Output String = "abca".

Now the queue is empty and we will stop this process and now we will check if the length of output string is equal the length of the input string.
As you can see in this case both of the strings are of equal length hence the output generated is correct and no two adjacent characters are same.

Final Output String = "abca".

Implementation in Java:

Following is the implementation of our above approach in Java:

package genus.open;

import java.util.Comparator;
import java.util.PriorityQueue;

//Creating a class to store our key data
class Key{
    char character;
    int freq;

    Key(char character, int freq){
        this.character = character;
        this.freq = freq;
    }
}
//Implementing our comparator to compare the keys
class KeyComparator implements Comparator<Key>{
    public int compare(Key key1, Key key2){
        if(key1.freq < key2.freq){
            return 1;
        }else if(key1.freq > key2.freq) {
            return -1;
        } return 0;
    }
}

public class Main {
    //this method rearranges string so two adjacent characters are not same
    static void rearrangeString(String string){
        int len = string.length();
        //creating an array to store the count of the characters
        int[] characterCount = new int[26];
        //loop to find and set the values of the array
        for(int i = 0; i < len; i++){
            characterCount[string.charAt(i) - 97] += 1;
        }

        PriorityQueue<Key> pQueue = new PriorityQueue<>(new KeyComparator());

        //adding keys to our priority queue if the count of that character is > 0
        for(int i = 97; i <= 'z'; i++){
            if((characterCount[i-97]) > 0){
                pQueue.add(new Key((char)i, characterCount[i-97]));
            }
        }

        string = "";

        Key prev = new Key('#', -1);

        while(pQueue.size() > 0) {
            Key k = pQueue.poll();//this method removes and returns the an element from the head of the queue
            string += k.character;

            if (prev.freq > 0) {
                pQueue.add(prev);
            }

            k.freq -= 1;
            prev = k;
        }

        if(string.length() != len){
            System.out.println("NOT POSSIBLE");
        }else{
            System.out.println(string);
        }
    }

    public static void main(String[] args) {
        String s = "aabbcadb";
        rearrangeString(s);
    }
}

As you can see in the above code we have created a class named Key to store our key data(character and frequency), then we have created another class KeyComparator which is nothing but a comparator which compares the frequency of the given keys.
Next we have created our Main class which contains our main method and rearrageString method, it is this method where the actual logic is implemented.

Output: ababcabd

Time Complexity

Time complexity of our approach: O(N log N)

In our main method we have two for loops in which the first loop has a time complexity of O(n), second loop has time complexity of O(nlogn) as adding an element in the priority queue takes log(n) time. And in the third loop where we are removing and again adding an element the time complexity is again O(nlogn).
Hence after adding all these we get O(nlogn).

With this article at OpenGenus, you have the complete knowledge of solving this problem. Enjoy.