Reading time: 35 minutes

Example:

Lets say we have an array of 4 elements :{4, 7, 1, 5, 2} and we have to insert all the elements in the max-priority queue.

First as the priority queue is empty, so 4 will be inserted initially.
Now when 7 will be inserted it will moved to front as 7 is greater than 4.
While inserting 1, as it is the current minimum element in the priority queue, it will remain in the back of priority queue.

Now 5 will be inserted between 7 and 4 as 5 is smaller than 7.

Now 2 will be inserted between 4 and 1 as it is smaller than 4 but greater than 1.

All the steps are represented in the diagram below:

Priority queue can be implemented by:

• Using Array/List
• Using Heap

1. Using Array/List:

A simple implementation is to use array of following structure.

struct item 
{
    int item; 
    int priority;
}

Suppose we have n elements and we have to insert these elements in the priority queue. We can use list and can insert elements in O(n) time and can sort them to maintain a priority queue in O(nlog₂n) time.

2. Using Heap:

We can use heaps to implement the priority queue.
It will take O(log₂n) time to insert and delete each element in the priority queue.

Based on heap structure, priority queue also has two types max-priority queue and min-priority queue.

There are several specialized heap data structures that either supply additional operations or outperform heap-based implementations for specific types of keys, specifically integer keys.

Examples:

• Binary Heap
• Binomial heap
• Fibonacci heap etc.

Here we will focus only on implementing max-priority queue using Binary heap (Max-Heap). Doing so, we maintain the Max-Heap property, which is value of any node in the max-heap tree is greater than both of its child.

Operations

A typical priority queue supports following operations.

• Insert(Item, Priority)
• GetHighestPriority()
• DeleteHighestPriority()
• IncreasePriority(Index, NewPriority)

1. Insert(Item, Priority)

Inserting a new element takes O(log₂n) time. We add a new item with given priority at the end of the tree. If new item's priority is less than its parent, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property. To regain the property, we shift up the element to its proper position.

// Inserts a new Item with priority p
Insert(int item, int p) 
{ 
    if (heap_size == capacity) 
    { 
        cout << "\nOverflow: Could not insert Item\n"; 
        return; 
    } 
  
    // First insert the new key at the end 
    heap_size++; 
    int i = heap_size - 1; 
    harr[i].val = item; 
    harr[i].priority = p;
  
    // Fix the max heap property if it is violated (shift up)
    while (i != 0 && harr[parent(i)].priority < harr[i].priority) 
    { 
       swap(&harr[i], &harr[parent(i)]); 
       i = parent(i); 
    } 
} 

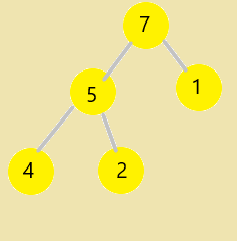
Example:

Initially there are 5 elements in priority queue.
Now lets insert a new item with priority 6.
In the diagram below, inserting another element having value 6 is violating the property of max-priority queue, so it is swapped with its parent having value 1, thus maintaining the max priority queue.

2. GetHighestPriority()

It returns the root element or the maximum priority element of Max Heap. Time Complexity of this operation is O(1) as we do no modify the heap.

 // Returns the maximum priority element (key at root) from max heap 
int GetHighestPriority() 
{
   return harr[0]; 
} 

3. DeleteHighestPriority()
In this operation, the maximum priority element will be removed and the last element of heap will be placed at index 0 and max_heapify will be performed on node 0 as placing last element on index 0 will violate the property of max-heap. Time Complexity of this Operation is O(log₂n).

// Method to remove highest priority element (or root) from max heap 
void DeleteHighestPriority() 
{ 
    if (heap_size <= 0) 
    {
        cout<< "Can’t remove element as queue is empty";
        return ; 
    }
    if (heap_size == 1) 
    { 
        heap_size--; 
        return ;
    } 
    harr[0] = harr[heap_size-1]; 
    heap_size--; 
    MaxHeapify(0); 
} 

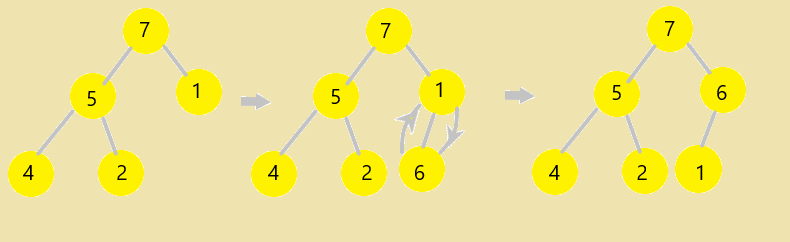
Example:

Lets remove the highest priority element, which is 7 from the tree.
Now 7 is replaced with last node of tree, which is 1.
In the diagram below, root node of tree is violating the property of max-priority queue, to maintain it we call MaxHeapify() procedure at index 0(i.e. root node) i.e. we shift down the element to its correct position.
By calling MaxHeapify() it recursively calls itself to regain the max-priority queue property.

4. IncreasePriority(Index, NewPriority)

If the new priority value of a node is less than the parent of the node, then we don’t need to do anything. Otherwise, we need to traverse up to fix the violated heap property. Time complexity of this operation is O(log₂n).

// Increases priority at index 'i' to NewPriority. 
IncreasePriority(int i, int NewPriority ) 
{ 
   if(NewPriority < harr[i].priority) 
   {
       cout<<"New value is less than current value, can’t be Updated" <<endl;
       return;
   }
   harr[i].priority = NewPriority; 
   while (i != 0 && harr[parent(i)].priority < harr[i].priority) 
   { 
       swap(&harr[i], &harr[parent(i)]); 
       i = parent(i); 
   } 
} 

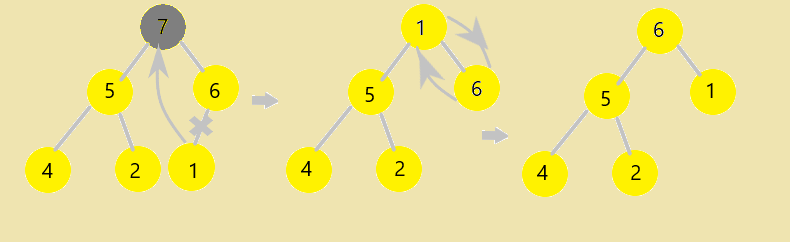
Example:

Lets increase the priority of the element at position 1 i.e. the element having priority 5 to 9.
Now it is violating the max-heap property, so to regain the property we shift up the element to its correct position i.e. we swap it with its parent(here root) element as the parent element has a priority of 7 which is less than the new priority assigned to it.

Complexity

The complexity of operations of priority queue implemented by Binary Heap (Max-Heap):

Time Complexity

1. Insert(): It takes O(log₂n) time per operation.
2. GetHighestPriority(): It takes O(1) time per operation.
3. DeleteHighestPriority(): It takes O(log₂n) time per operation.
4. IncreasePriority(): It takes O(log₂n) time per operation.

Space Complexity
It takes O(n) space complexity.
where n is total number of elements.

Implementation

code in C++ 14

// A C++ program to demonstrate common pririty Queue Operations using Binary Heap
#include<iostream> 
#include<climits> 
using namespace std; 
// A node element having some Value(name) and Priority
struct node
{
    char val;
    int priority;
};
// Prototype of a utility function to swap two integers 
void swap(node *x, node *y); 
// A class for Max Heap 
class MaxHeap
{ 
    node *harr; // pointer to array of elements in heap 
    int capacity; // maximum possible size of max heap 
    int heap_size; // Current number of elements in max heap 
public: 
    // Constructor 
    MaxHeap(int capacity); 
  
    // to heapify a subtree with the root at given index 
    void MaxHeapify(int ); 
      
     // to get index of parent of node at index i
    int parent(int i) { return (i-1)/2; } 
  
    // to get index of left child of node at index i 
    int left(int i) { return (2*i + 1); } 
  
    // to get index of right child of node at index i 
    int right(int i) { return (2*i + 2); } 
  
    // Increases priority value of node at index i to NewPriority 
    void IncreasePriority(int i, int NewPriority); 
  
    // Returns the maximum priority element (key at root) from max heap 
    node GetHighestPriority() {
    return harr[0]; 
    }
  
    // Deletes the highest priority element(key at root). 
    void DeleteHighestPriority(); 
  
    // Inserts a new Item with Priority p 
    void Insert(char Item,int p); 
}; 
  
// Constructor: Builds a heap from a given array a[] of given size 
MaxHeap::MaxHeap(int cap) 
{ 
    heap_size = 0; 
    capacity = cap; 
    harr = new node[cap]; 
} 
  
// Inserts a new Item with priority p
void MaxHeap::Insert(char item, int p) 
{ 
    if (heap_size == capacity) 
    { 
        cout << "\nOverflow: Could not insert Item\n"; 
        return; 
    } 
  
    // First insert the new key at the end 
    heap_size++; 
    int i = heap_size - 1; 
    harr[i].val = item; 
    harr[i].priority = p;
  
    // Fix the max heap property if it is violated 
    while (i != 0 && harr[parent(i)].priority < harr[i].priority) 
    { 
       swap(&harr[i], &harr[parent(i)]); 
       i = parent(i); 
    } 
} 
  
// Increases priority at index 'i' to NewPriority. 
void MaxHeap::IncreasePriority(int i, int NewPriority ) { 
  if(NewPriority < harr[i].priority) {
      cout<<"New value is less than current value, can’t be Updated" <<endl;
       return;
       }
   harr[i].priority = NewPriority; 
   while (i != 0 && harr[parent(i)].priority < harr[i].priority) 
   { 
       swap(&harr[i], &harr[parent(i)]); 
       i = parent(i); 
   } 
}  

// Method to remove highest priority element (or root) from max heap 
void MaxHeap::DeleteHighestPriority()
{ 
    if (heap_size <= 0) {
    cout<< "Can’t remove element as queue is empty";
        return ; 
        }
    if (heap_size == 1) 
    { 
        heap_size--; 
        return ;
    } 
    harr[0] = harr[heap_size-1]; 
    heap_size--; 
    MaxHeapify(0); 
} 

// A recursive method to heapify a subtree with the root at given index 
// This method assumes that the subtrees are already heapified 
void MaxHeap::MaxHeapify(int i) 
{ 
    int l = left(i); 
    int r = right(i); 
    int largest = i; 
    if (l < heap_size && harr[l].priority > harr[i].priority) 
        largest = l; 
    if (r < heap_size && harr[r].priority > harr[largest].priority) 
        largest = r; 
    if (largest != i) 
    { 
        swap(&harr[i], &harr[largest]); 
        MaxHeapify(largest); 
    } 
} 
  
// A utility function to swap two elements 
void swap(node *x, node *y) 
{ 
    node temp = *x; 
    *x = *y; 
    *y = temp; 
} 
  
// Driver program to test above functions 
int main() 
{   
    MaxHeap h(11); 
    h.Insert('A',3); 
    h.Insert('B',5);  
    h.Insert('C',2); 
    h.Insert('D',4); 
    h.Insert('E',9); 
    h.Insert('F',15);
    node temp;
    temp = h.GetHighestPriority();
    cout << temp.val << " ";
    h.DeleteHighestPriority();
    temp=h.GetHighestPriority();
    cout << temp.val << " "; 
    h.IncreasePriority(2, 25); 
    temp=h.GetHighestPriority();
    cout << temp.val ; 
    return 0; 
} 

Applications

1. CPU Scheduling
2. Graph algorithms like Dijkstra’s shortest path algorithm, Prim’s Minimum Spanning Tree, etc.
3. All queue applications where priority is involved.

References

• See the chapter 6 in [CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms (3rd Edition). MIT Press and McGraw-Hill. 2009.