
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 40 minutes
Binomial Heap is an extension of Binary Heap that provides faster union or merge operation together with other operations provided by Binary Heap. A Binomial Heap is a collection of Binomial trees. Binomial Heap is used to implement priority queues.
Binomial Trees
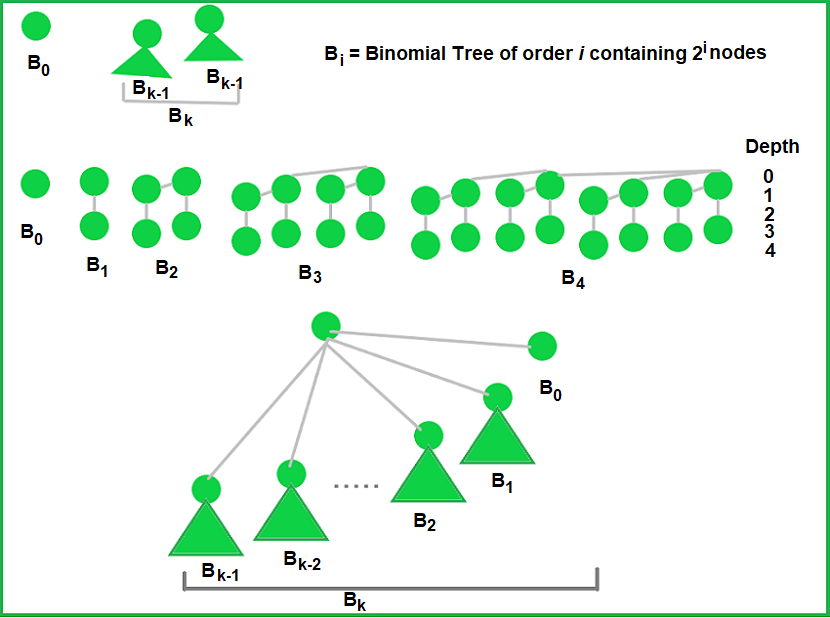
A Binomial Tree is a unique structure tree which follows the following properties:
- A Binomial Tree of order 0 has exactly 1 node.
- A Binomial Tree of order k can be constructed by taking two binomial trees of order k-1 and making one as leftmost child or other.
A Binomial Tree of order k has following properties:
- It has exactly 2k nodes.
- It has a depth or height of k.
- There are exactly kCi nodes at depth(height) i, for i=0, 1, 2, .....k-1, k.
- The root of tree has degree k and children of root are themselves are binomial trees of order k-1, k-2, ....1, 0 from left to right.
Binomial Heap
A Binomial Heap is a set of Binomial Trees which follows Binomial Heap Property.
Binomial Heap Property
- Every binomial tree in a binomial min heap obeys the min-heap property (that the key of a node is greater than or equal to the key of its parent) and every binomial tree in a binomial max heap obeys the max-heap property (that the key of a node is less than or equal to the key of its parent).
- There can only be either one or zero binomial trees for each order. In other words, for every k, there is at most one binomial tree of order k in the heap.
Example:
Lets take an example of Binomial Heap of 13 nodes, it is a collection of 3 Binomial trees of order 0, 2 and 3.
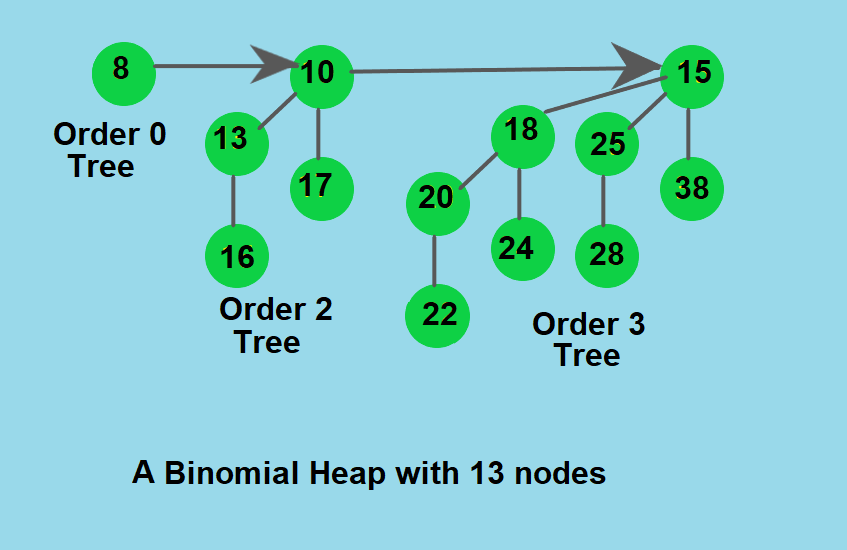
Here in the diagram each node of the tree is following the Min Heap property in its own Binomial Tree. As 15 is the smallest element and root of the order 3 Binomial tree, 10 is the smallest element and root of the order 2 Binomial Tree and 8 is the root of the order 0 Binomial Tree.
We merge these three trees to get the Binomial Heap of 13 nodes.
Now the question is how should we know the orders of different trees required for a n nodes Binomial Heap?
The solution of this problem lies within the Binary representation of n.
Binary Representation of a number and Binomial Heaps
A Binomial Heap with n nodes has the number of Binomial Trees equal to the total number of set bits in the Binary representation of n. For example let n be 13, here 3 set bits in the binary representation of 13 (00001101), hence 3 Binomial Trees required. We can also relate the degree of these Binomial Trees with positions of set bits. With this relation, we can conclude that there are O(log2n) Binomial Trees in a Binomial Heap with n nodes as a number n can be represented in binary with log2n binary digits.
Operations
The main operation in Binomial Heap is union(), all other operations mainly use this operation. The union() operation is to combine two Binomial Heaps into one.
The Basic operations of the Binomial Heap are as follows:
- Union(H1, H2) or Merge(H1, H2)
- Insert(k)
- GetMin()
- ExtractMin()
- DecreaseKey(x, k)
- Delete(x)
1. Union(H1, H2) or Merge(H1, H2)
The simplest and most important operation is the merging(union) of two binomial trees of the same order within a binomial heap. Due to the structure of binomial trees, they can be merged trivially. As their root node is the smallest element within the tree, by comparing the two keys, the smaller of them is the minimum key, and becomes the new root node. Then the other tree becomes a subtree of the combined tree. This operation is basic to the complete merging of two binomial heaps.
-
The first step is to simply merge the two Heaps in non-decreasing order of degrees. In the following diagram, figure(b) shows the result after merging.
-
After the simple merge, we need to make sure that there is at most one Binomial Tree of any order. To do this, we need to combine Binomial Trees of the same order. We traverse the list of merged roots, we keep track of three-pointers, prev, x and next-x. There can be following 4 cases when we traverse the list of roots.
- Case 1: Orders of x and next-x are not same, we simply move ahead.
In following 3 cases orders of x and next-x are same. - Case 2: If the order of next-next-x is also same, move ahead.
- Case 3: If the key of x is smaller than or equal to the key of next-x, then make next-x as a child of x by linking it with x.
- Case 4: If the key of x is greater, then make x as the child of next.
- Case 1: Orders of x and next-x are not same, we simply move ahead.
// This function perform union operation on two
// binomial heap i.e. h1 & h2
list<Node *> Union(list<Node *> &h1,
list<Node *> &h2)
{
// _new to another binomial heap which contain
// new heap after merging h1 & h2
list<Node *> _new;
list<Node *>::iterator it = h1.begin();
list<Node *>::iterator ot = h2.begin();
while (it != h1.end() && ot != h2.end())
{
// if D(h1) <= D(h2)
if ((*it)->degree <= (*ot)->degree)
{
_new.push_back(*it);
it++;
}
// if D(h1) > D(h2)
else
{
_new.push_back(*ot);
ot++;
}
}
// if there remains some elements in h1 binomial heap
while (it != h1.end())
{
_new.push_back(*it);
it++;
}
// if there remains some elements in h2 binomial heap
while (ot != h2.end())
{
_new.push_back(*ot);
ot++;
}
return _new;
}
2. Insert(k)
Inserting a new element to a heap can be done by simply creating a new heap containing only this element and then merging it with the original heap. Due to the merge, insert takes O(log n) time. However, across a series of n consecutive insertions, insert has an amortized time of O(1).
// Utility Function for inserting a Binomial Tree into binomial heap
void insertTree(Node *tree)
{
// creating a new heap i.e temp
list<Node *> temp;
// inserting Binomial Tree into heap
temp.push_back(tree);
// perform union operation to finally insert
// Binomial Tree in original heap
heap = Union(heap, temp);
adjust();
}
// Function for inserting a key into the binomial heap
void insert(int key)
{
Node *temp = newNode(key);
insertTree(temp);
}
3. GetMin()
A simple way to getMin() is to traverse the list of root of Binomial Trees and return the minimum key. This implementation requires O(logn) time. It can be optimized to O(1) by maintaining a pointer to minimum key root.
A simple way to getMin() is to traverse the list of root of Binomial Trees and return the minimum key. This implementation requires O(log n) time. It can be optimized to O(1) by maintaining a pointer to minimum key root.
The pointer must be updated when performing any operation other than Find minimum. This can be done in O(log n) without raising the running time of any operation.
// Function to get the Min-value
// present in the binomial heap
Node *getMin()
{
list<Node *>::iterator it = heap.begin();
Node *temp = *it;
while (it != heap.end())
{
if ((*it)->data < temp->data)
temp = *it;
it++;
}
return temp;
}
4. ExtractMin()
To extract the minimum element from the heap, first find this element by GetMin(), remove it from its binomial tree, and obtain a list of its subtrees. Then transform this list of subtrees into a separate binomial heap by reordering them from smallest to largest order. Then merge this heap with the original heap. Since each root has at most log n children, creating this new heap is O(log n). Merging heaps is
O(log n), so the entire ExtractMin() operation is O(log n).
// Function to delete the Minimum element of Binomial Heap
void extractMin()
{
list<Node *> newheap, lo;
Node *temp;
// temp contains the pointer of minimum value
// element in heap
temp = getMin();
list<Node *>::iterator it;
it = heap.begin();
while (it != heap.end())
{
if (*it != temp)
{
// inserting all Binomial Tree into new
// binomial heap except the Binomial Tree
// contains minimum element
newheap.push_back(*it);
}
it++;
}
lo = removeMinTree(temp);
heap = Union(newheap, lo);
adjust();
}
5. DecreaseKey(x, k)
After decreasing the key of an element, it may become smaller than the key of its parent, violating the minimum-heap property. If this is the case, we exchange the element with its parent, and possibly also with its grandparent, and so on, until the minimum-heap property is no longer violated. Each binomial tree has height at most log n, so this takes O(log n) time.
// Function to decrease the value of old_val
// to new_val
void decreaseKey( int old_val,
int new_val)
{
// First check element present or not
list<Node *>::iterator it=heap.begin();
Node *node = NULL;
while (it != heap.end() && node == NULL)
{
node = findNode(*it, old_val);
it++;
}
// return if Node is not present
if (node == NULL)
return;
// Reduce the value to the minimum
node->data = new_val;
Node *parent = node->parent;
// Update the heap according to reduced value
while (parent != NULL && node->data < parent->data)
{
swap(node->data, parent->data);
node = parent;
parent = parent->parent;
}
}
6. Delete(x)
To delete an element from the heap, decrease its key to negative infinity (that is, some value lower than any element in the heap) and then delete the minimum in the heap by calling ExtractMin().
// Function to delete an element
void Delete(int val)
{
// Reduce the value of element to minimum
decreaseKey(val, INT_MIN);
// Delete the minimum element from heap
extractMin();
}
Example:
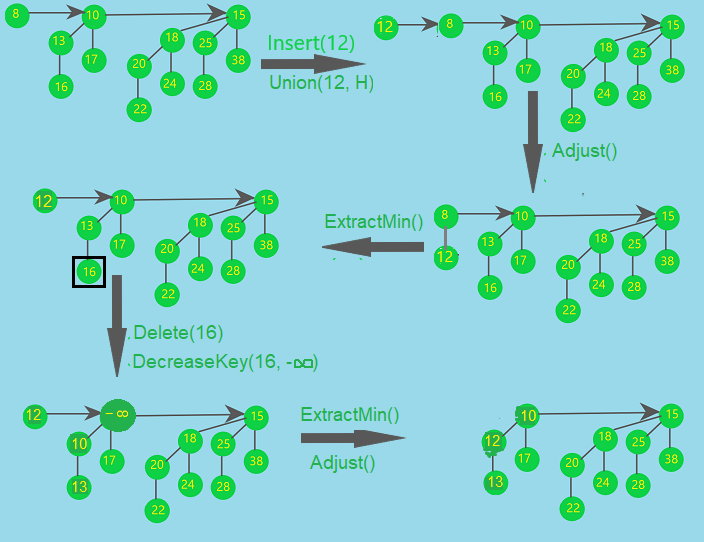
let's take an example to understand different operations of Binomial Heap.
In the given diagram a Binomial Heap is given now let's insert 12 to the Heap,
to do so we create a new heap with element only 12 and then merge it with the original Heap. After merging them we need to adjust the heap so that it satisfies the min-heap property and there should exists at most one tree of any order to do so we call adjust() function.
Now let's delete the minimum element which is 8 that can be found by calling GetMin() function then we remove the element and remove the containing tree also, then we rebuild that tree and merge it with the original Heap to get the overall binomial heap.
Now let's delete the element 16, to do so we find the element and then decrease the key to negative infinity so that it becomes the overall minimum of the heap then we remove it from heap by calling extractMin(). Now we adjust the tree to maintain min-heap and binomial heap properties.
Complexity
The complexity of operations of Binomial Heap (Min-Heap):
Time Complexity
- Insert(): It takes O(1) (Amortized) O(log n) (worst-case) time per operation.
- Union(): It takes O(log n) time per operation.
- GetMin(): It takes O(log n) time per operation.
- ExtractMin(): It takes O(log n) time per operation.
- DecreaseKey(): It takes O(log n) time per operation.
- Delete(): It takes O(log n) time per operation
Space Complexity
It takes O(n) space complexity.
Implementation
Code in C++
// C++ program to implement different operations on Binomial Heap
#include<iostream>
#include<list>
#include<algorithm>
#include<climits>
using namespace std;
// A Binomial Tree node.
struct Node
{
int data, degree;
Node *child, *sibling, *parent;
};
class BHeap
{
list<Node*> heap;
public:
Node *newNode(int key)
{
Node *temp = new Node;
temp->data = key;
temp->degree = 0;
temp->child = temp->parent = temp->sibling = NULL;
return temp;
}
// This function merge two Binomial Trees.
Node *mergeBTrees(Node *b1, Node *b2)
{
// Make sure b1 is smaller
if (b1->data > b2->data)
swap(b1, b2);
// We basically make larger valued tree
// a child of smaller valued tree
b2->parent = b1;
b2->sibling = b1->child;
b1->child = b2;
b1->degree++;
return b1;
}
// This function perform union operation on two
// binomial heap i.e. h1 & h2
list<Node *> Union(list<Node *> &h1,
list<Node *> &h2)
{
// _new to another binomial heap which contain
// new heap after merging h1 & h2
list<Node *> _new;
list<Node *>::iterator it = h1.begin();
list<Node *>::iterator ot = h2.begin();
while (it != h1.end() && ot != h2.end())
{
// if D(h1) <= D(h2)
if ((*it)->degree <= (*ot)->degree)
{
_new.push_back(*it);
it++;
}
// if D(h1) > D(h2)
else
{
_new.push_back(*ot);
ot++;
}
}
// if there remains some elements in h1 binomial heap
while (it != h1.end())
{
_new.push_back(*it);
it++;
}
// if there remains some elements in h2 binomial heap
while (ot != h2.end())
{
_new.push_back(*ot);
ot++;
}
return _new;
}
// adjust function rearranges the heap so that
// heap is in increasing order of degree and
// no two binomial trees have same degree in this heap
void adjust()
{
if (heap.size() <= 1)
return ;
list<Node *> newheap;
list<Node *>::iterator it1, it2, it3;
it1 = it2 = it3 = heap.begin();
if (heap.size() == 2)
{
it2 = it1;
it2++;
it3 = heap.end();
}
else
{
it2++;
it3 = it2;
it3++;
}
while (it1 != heap.end())
{
// if only one element remains to be processed
if (it2 == heap.end())
it1++;
// If D(it1) < D(it2) i.e. merging of Binomial
// Tree pointed by it1 & it2 is not possible
// then move next in heap
else if ((*it1)->degree < (*it2)->degree)
{
it1++;
it2++;
if (it3 != heap.end())
it3++;
}
// if D(it1),D(it2) & D(it3) are same i.e.
// degree of three consecutive Binomial Tree are same
// in heap
else if (it3 != heap.end() &&
(*it1)->degree == (*it2)->degree &&
(*it1)->degree == (*it3)->degree)
{
it1++;
it2++;
it3++;
}
// if degree of two Binomial Tree are same in heap
else if ((*it1)->degree == (*it2)->degree)
{
Node *temp;
*it1 = mergeBTrees(*it1, *it2);
it2 = heap.erase(it2);
if (it3 != heap.end())
it3++;
}
}
}
// inserting a Binomial Tree into binomial heap
void insertTree(Node *tree)
{
// creating a new heap i.e temp
list<Node *> temp;
// inserting Binomial Tree into heap
temp.push_back(tree);
// perform union operation to finally insert
// Binomial Tree in original heap
heap = Union(heap, temp);
adjust();
}
// inserting a key into the binomial heap
void insert(int key)
{
Node *temp = newNode(key);
insertTree(temp);
}
// removing minimum key element from binomial heap
// this function take Binomial Tree as input and return
// binomial heap after
// removing head of that tree i.e. minimum element
list<Node *> removeMinTree(Node *tree)
{
list<Node *> _heap;
Node *temp = tree->child;
Node *lo;
// making a binomial heap from Binomial Tree
while (temp)
{
lo = temp;
temp = temp->sibling;
lo->sibling = NULL;
_heap.push_front(lo);
}
return _heap;
}
// return pointer of minimum value Node
// present in the binomial heap
Node *getMin()
{
list<Node *>::iterator it = heap.begin();
Node *temp = *it;
while (it != heap.end())
{
if ((*it)->data < temp->data)
temp = *it;
it++;
}
return temp;
}
// Function to delete the Minimum element of Binomial Heap
void extractMin()
{
list<Node *> newheap, lo;
Node *temp;
// temp contains the pointer of minimum value
// element in heap
temp = getMin();
list<Node *>::iterator it;
it = heap.begin();
while (it != heap.end())
{
if (*it != temp)
{
// inserting all Binomial Tree into new
// binomial heap except the Binomial Tree
// contains minimum element
newheap.push_back(*it);
}
it++;
}
lo = removeMinTree(temp);
heap = Union(newheap, lo);
adjust();
}
// Function to search for an element
Node * findNode(Node * it, int val)
{
if (it == NULL)
return NULL;
// check if key is equal to the root's data
if (it->data == val)
return it;
/*// if value is less than root's data then it is not in this tree
// because it follows Min-Heap property
if(it->data > val)
return NULL;
*/
// Recur for child
Node *res = findNode(it->child, val);
if (res != NULL)
return res;
return findNode(it->sibling, val);
}
// Function to decrease the value of old_val
// to new_val
void decreaseKey( int old_val,
int new_val)
{
// First check element present or not
list<Node *>::iterator it=heap.begin();
Node *node = NULL;
while (it != heap.end() && node == NULL)
{
node = findNode(*it, old_val);
it++;
}
// return if Node is not present
if (node == NULL)
return;
// Reduce the value to the minimum
node->data = new_val;
Node *parent = node->parent;
// Update the heap according to reduced value
while (parent != NULL && node->data < parent->data)
{
swap(node->data, parent->data);
node = parent;
parent = parent->parent;
}
}
// Function to delete an element
void Delete(int val)
{
// Reduce the value of element to minimum
decreaseKey(val, INT_MIN);
// Delete the minimum element from heap
extractMin();
}
// print function for Binomial Tree
void printTree(Node *h)
{
while (h)
{
cout << h->data << " ";
printTree(h->child);
h = h->sibling;
}
}
// print function for binomial heap
void printHeap()
{
list<Node *>::iterator it;
it = heap.begin();
while (it != heap.end())
{
printTree(*it);
it++;
}
cout<<"\n";
}
};
// Driver program to test above functions
int main()
{
int ch,key;
BHeap H;
H.insert(10);
H.insert(20);
H.insert(30);
H.insert(40);
H.insert(50);
cout<< "Heap elements after insertion:\n";
H.printHeap();
Node *temp = H.getMin();
cout << "Minimum element of heap "
<< temp->data << "\n";
// Decrease key of 30 to 8
H.decreaseKey(30, 8);
temp = H.getMin();
cout << "Now Minimum element of heap "<< temp->data << "\n";
// Delete minimum element of heap
H.extractMin();
cout << "Heap after deletion of minimum element\n";
H.printHeap();
H.Delete(20);
cout << "Heap after deletion of 20\n";
H.printHeap();
return 0;
}
Applications
- Discrete event simulation
A discrete-event simulation (DES) models the operation of a system as a (discrete) sequence of events in time. - Implementation of Priority queues
We prefer Binomial Heap over Binary heap for implementing priority queues as Binomial Heap provides faster merge operation(O(log n) than O(n)) and also it gives amortized insert time of O(1) than O(log n) of Binary heap. - Network Bandwidth management
Priority queuing can be used to manage limited resources such as bandwidth on a transmission line from a network router.
References
- See the chapter 19 in [CLRS] Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms (3rd Edition). MIT Press and McGraw-Hill. 2009.
