
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
In this article, we will solve Subset Sum problem using a recursive approach where the key idea is to generate all subset recursively. It will take O(2^N) time complexity.
Subset sum problem is that a subset A of n positive integers and a value sum is given, find whether or not there exists any subset of the given set, the sum of whose elements is equal to the given value of sum.
Example:
Given the following set of positive numbers:
{ 2, 9, 10, 1, 99, 3}
We need to find if there is a subset for a given sum say 4:
{ 1, 3 }
For another value say 5, there is another subset:
{ 2, 3}
Similarly, for 6, we have {2, 1, 3} as the subset.
For 7, there is no subset where the sum of elements equal to 7.
This problem can be solved using following algorithms:
- Recursive method
- Backtracking
- Dynamic Programing
In this article, we will solve this using a recursive approach.
Recursive method
The Subset sum problem can be divided into two cases:
- We include current element in subset and recurse the remaining elements within remaining sum
- We exclude current element from subset and recurse for remaining elements.
- Finally, we return true if we get subset by including or excluding current item else we return false.
The base case of the recursion would be when no items are left or sum becomes negative. We return true when sum becomes 0 i.e. subset is found.
Pseudocode:
boolean subset_sum(list, starting_index, sum)
{
if (sum == 0)
return true;
if (length(list) - starting_index == 1)
if(list[0] == sum)
return true;
else
return false;
boolean result_1 = subset_sum(list, starting_index + 1, sum - list[starting_index);
boolean result_2 = subset_sum(list, starting_index + 1, sum);
return result_1 | result_2;
}
Example
Consider the following array/ list of integers:
{1, 3, 2}
We want to find if there is a subset with sum 3.
Note that there are two such subsets {1, 2} and {3}. We will follow our recursive approach.
We will maintain a stack of calls which is empty {} intially.
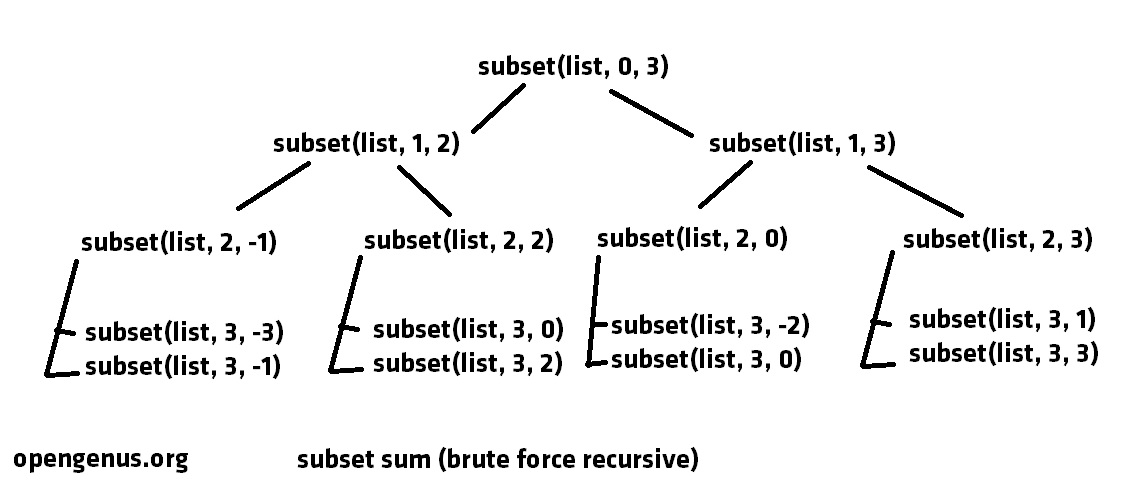
Step 1: subset(list, 0, 3)
The call is subset(list, 0, 3)
Call stack { subset(list, 0, 3) }
Let us start with element at index 0: 1
There will be two calls:
subset(list, 1, 2) : case in which 1 is added
subset(list, 1, 3) : case in which 1 is ignored
Call stack: { subset(list, 0, 3), subset(list, 1, 2), subset(list, 1, 3) }
Step 2: subset(list, 1, 3)
Call stack: { subset(list, 0, 3), subset(list, 1, 2), subset(list, 1, 3) }
We consider element at index 1: 3 which results in two calls:
subset(list, 2, 0): case when 3 is considered (as sum == 0, found)
subset(list, 2, 3): case when 3 is ignored
Consider subset(list, 2, 3) where element at index 2 is 2 and gives rise to:
subset(list, 3, 1): where 2 is considered
subset(list, 3, 3): where 2 is ignored
As we have reached the end, this path gave rise to one true for {3}
Step 3: subset(list, 1, 2)
We consider element at index 1: 3 which results in two calls:
subset(list, 2, -1): case when 3 is considered (as sum == 0, found)
subset(list, 2, 2): case when 3 is ignored
Consider subset(list, 2, 2) where element at index 2 is 2 and gives rise to:
subset(list, 3, 0): where 2 is considered (as sum == 0, we found a result)
subset(list, 3, 2): where 2 is ignored
For the other path subset(list, 2, -1), we can skip this as the sum has become negative.
As we have reached the end, this path gave rise to one true for {1, 2}
Following diagram captures the idea:
Implementation
Following is the implementation in Java for our recursive approach for SubSet sum problem:
// Part of OpenGenus IQ
class subset_sum_recursive
{
static boolean subset_sum_util(int list[], int starting_index, int sum)
{
if (sum == 0)
return true;
if (list.length - starting_index == 1)
if(list[starting_index] == sum)
return true;
else
return false;
boolean result_1 = subset_sum_util(list, starting_index + 1, sum - list[starting_index]);
boolean result_2 = subset_sum_util(list, starting_index + 1, sum);
return result_1 | result_2;
}
static boolean subset_sum(int list[], int sum)
{
if(list.length < 1)
return false;
if(list.length == 1)
if(list[0] == sum)
return true;
else
return false;
return subset_sum_util(list, 0, sum);
}
public static void main (String[] args)
{
int list[] = {2, 1, 99, 3};
System.out.println(subset_sum(list, 7));
}
}
Following is the implementation in C++:
/* Part of Cosmos by OpenGenus Foundation */
#include<iostream>
using namespace std;
/*
*Find whether or not there exists any subset
* of array that sum up to targetSum
*/
class Subset_Sum
{
public:
// RECURSIVE METHOD
bool subsetSum_Recursive(int arr[], int n, int sum)
{
if (sum == 0)
return true
if (n < 0 || sum < 0)
return false;
bool include = subsetSum_Recursive(arr, n - 1, sum - arr[n]);
bool exclude = subsetSum_Recursive(arr, n - 1, sum);
return include || exclude;
}
};
int main()
{
int i, n, sum;
Subset_Sum S;
cout << "Enter the number of elements in the set" << endl;
cin >> n;
int a[n];
cout << "Enter the values" << endl;
for(i=0;i<n;i++)
cin>>a[i];
cout << "Enter the value of sum" << endl;
cin >> sum;
bool f = false;
S.subsetSum_Recursive(a, n, sum);
if (f)
cout << "subset with the given sum found" << endl;
else
cout << "no required subset found" << endl;
return 0;
}
Complexity
-
Worst case time complexity:
Θ(2^n) -
Space complexity:
Θ(1)
