
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 30 minutes | Coding time: 10 minutes
In this article, we will solve Subset Sum problem using a backtracking approach which will take O(2^N) time complexity but is significantly faster than the recursive approach which take exponential time as well.
Subset sum problem is the problem of finding a subset such that the sum of elements equal a given number. The backtracking approach generates all permutations in the worst case but in general, performs better than the recursive approach towards subset sum problem.
A subset A of n positive integers and a value sum is given, find whether or not there exists any subset of the given set, the sum of whose elements is equal to the given value of sum.
Example:
Given the following set of positive numbers:
{ 2, 9, 10, 1, 99, 3}
We need to find if there is a subset for a given sum say 4:
{ 1, 3 }
For another value say 5, there is another subset:
{ 2, 3}
Similarly, for 6, we have {2, 1, 3} as the subset.
For 7, there is no subset where the sum of elements equal to 7.
This problem can be solved using following algorithms:
- Recursive method
- Backtracking
- Dynamic Programing
In this article, we will solve this using Backtracking approach
Backtracking
In Backtracking algorithm as we go down along depth of tree we add elements so far, and if the added sum is satisfying explicit constraints, we will continue to generate child nodes further. Whenever the constraints are not met, we stop further generation of sub-trees of that node, and backtrack to previous node to explore the nodes not yet explored.We need to explore the nodes along the breadth and depth of the tree. Generating nodes along breadth is controlled by loop and nodes along the depth are generated using recursion (post order traversal).
Steps:
- Start with an empty set
- Add the next element from the list to the set
- If the subset is having sum M, then stop with that subset as solution.
- If the subset is not feasible or if we have reached the end of the set, then backtrack through the subset until we find the most suitable value.
- If the subset is feasible (sum of seubset < M) then go to step 2.
- If we have visited all the elements without finding a suitable subset and if no backtracking is possible then stop without solution.
Pseudocode
void subset_sum(int list[], int sum, int starting_index, int target_sum)
{
if( target_sum == sum )
{
subset_count++;
if(starting_index < list.length)
subset_sum(list, sum - list[starting_index-1], starting_index, target_sum);
}
else
{
for( int i = starting_index; i < list.length; i++ )
{
subset_sum(list, sum + list[i], i + 1, target_sum);
}
}
}
Example
Consider the following array/ list of integers:
{1, 3, 2}
We want to find if there is a subset with sum 3.
Note that there are two such subsets {1, 2} and {3}. We will follow our backtracking approach.
Consider our empty set {}
We add 1 to it {1} (sum = 1, 1 < 3)
We add 2 to it {1, 3} (sum = 3, 3 == 3, found)
We remove 3 from it {1} (sum = 1, 1 < 3)
We add 2 to it {1, 2} (sum = 3, 3 == 3, found)
We remove 2 and see that all elements have been considered.
Following diagram captures the idea:
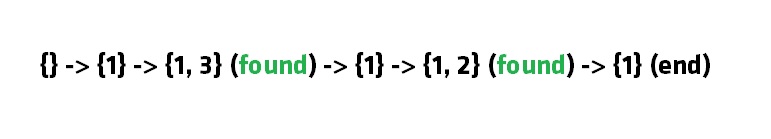
Implementations in Java and C++
Following is the implementation of the backtracking approach in Java:
public class subset_sum_backtrack
{
static int subset_count = 0;
static void subset_sum(int list[], int sum, int starting_index, int target_sum)
{
if( target_sum == sum )
{
subset_count++;
if(starting_index < list.length)
subset_sum(list, sum - list[starting_index-1], starting_index, target_sum);
}
else
{
for( int i = starting_index; i < list.length; i++ )
{
subset_sum(list, sum + list[i], i + 1, target_sum);
}
}
}
public static void main(String args[])
{
int list[] = {1, 3, 5, 2};
subset_sum(list, 0, 0, 6);
System.out.println(subset_count);
}
}
Following is the implementation in C++:
/* Part of Cosmos by OpenGenus Foundation */
#include<iostream>
using namespace std;
/*
*Find whether or not there exists any subset
* of array that sum up to targetSum
*/
class Subset_Sum
{
public:
// BACKTRACKING ALGORITHM
void subsetsum_Backtracking(int Set[] , int pos, int sum, int tmpsum, int size, bool & found)
{
if (sum == tmpsum)
found = true;
// generate nodes along the breadth
for (int i = pos; i < size; i++)
{
if (tmpsum + Set[i] <= sum)
{
tmpsum += Set[i];
// consider next level node (along depth)
subsetsum_Backtracking(Set, i + 1, sum, tmpsum, size, found);
tmpsum -= Set[i];
}
}
}
};
int main()
{
int i, n, sum;
Subset_Sum S;
cout << "Enter the number of elements in the set" << endl;
cin >> n;
int a[n];
cout << "Enter the values" << endl;
for(i=0;i<n;i++)
cin>>a[i];
cout << "Enter the value of sum" << endl;
cin >> sum;
bool f = false;
S.subsetsum_Backtracking(a, 0, sum, 0, n, f);
if (f)
cout << "subset with the given sum found" << endl;
else
cout << "no required subset found" << endl;
return 0;
}
Complexity
-
Worst case time complexity:
Θ(2^n) -
Space complexity:
Θ(1)
