Three address code

Three address code is generated by a compiler for code optimization, it uses a maximum of three addresses to represent any statement. In this article we discuss it.

Table of contents.

1. Introduction.
2. Addresses and instructions.
3. An implementation using quadruples.
4. An implementation using triples.
5. Static single assignment (SSA) form.
6. Summary.
7. References.

Introduction.

Three address code is an intermediate code used by optimizing compilers whereby a given expression is broken down into several separate instructions which can be easily translated into assembly language.

For example a source language expression a+b*c is translated into a sequence of three-address instruction as follows,

t1 = b * c
t2 = a + t1

t1 and t2 are compiler generated temporary names.
Three address code exhibits multi-operator arithmetic expressions and nested flow-of-control statements which makes it useful for generating and optimizing target code.

We can also view three-address code as a linearized representation of syntax to a directed acyclic graph(DAG) whereby names correspond to the interior nodes of the DAG as shown below.
An example

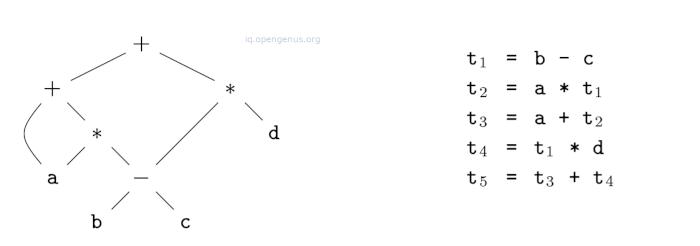
Addresses and instructions.

Three-address code involves addresses and instructions.

In object-oriented terms addresses will correspond to classes while instructions correspond to the appropriate subclasses.

An address can either be a name, constant or a compiler-generated temporary.
In a sequence of instructions symbolic labels will represent the index of a three-address instruction.

These symbolic labels are used by instructions which alter the flow of control.
Labels can be used in place of actual indexes by making a separate pass or by backpatching.

Forms of three-address instructions

1. Assignment in the form of a = b op c where op is a binary arithmetic or logical operation and a, b and c are addresses.
2. Assignments in the form a = op b where op is a unary operation. Essential unary operations include unary minus, logical negation and conversion operators.
3. Copy instructions in the form of a = b where a is assigned to the value of b.
4. An unconditional jump in the form of goto L. Instructions labeled L are next to be executed.
5. Conditional jumps in the form of if a goto L and ifFalse a goto L. These execute the instruction with label L next if a is true and false respectively, otherwise the following three-address instruction in the sequence is executed next.
6. Conditional jumps in the form of if a relop y goto L, These apply relational operators such as <, ==, >=, <= etc to a and b. If not the next instruction in the sequence is executed next.
7. Procedure calls and returns are implemented as follows, param a for parameters; call p, n and y = call p, n for procedure and function calls respectively. return y where y represents a return value.

An example

for the procedure call (a1, a2, ..., an) we have the following three address instructions;
param a1
param a2
...
param an
call p, n.
Where n is the number of actual parameters in call p, n.
n is not redundant since calls can be nested.

8. Indexed copy instructions in the form of a = b[i] and a[i] = b. An instruction a = b[i] sets a to the value in the location i memory units beyond location b and the instruction a[i] = b sets contents of location i units beyond a to the value of b.
9. Address and pointer assignments in the form of a = &b, a = * b and a = b. An instruction a = &b will set the right value of a to be the location of left value of $b^2$. Presumably b is a name(temporary) denoting an expression with left value such as A[i][j], a is a pointer or temporary whose right value is a location.
   right value of a is made equal to contents of that location. * a = b sets right value of the object pointed to by a to the right value.

An example
Given the statement,
do i = i+1; while (a[i] < v);

A possible translation would be;

L:    t1 = i + 1
      i = t1
      t2 = i * 8
      t3 = a[t2]
      if t3 < v goto L

From the above translation we use a symbolic label L attached to the first instruction.

or (position numbers)

100:    t1 = i + 1
101:    i = t1
102:    t2 = i * 8
103:    t3 = a[t2]
104:    if t3 < v goto L 

The above shows position numbers for the instructions starting at position 100.

In both translations, the last instruction is a conditional jump to the first instruction.
The multiplication i*8 is appropriate for an array of elements each taking 8 units of space.
Choice of allowed operators is an important factor in that the operator set must be rich enough to implement operations in the source language otherwise the optimizer and code generator must work harder to rediscover the structure and generate good code.

An implementation using quadruples.

The description of three-address instructions specifies components for each type of instructions however no data structure is specified.

In compilers these instructions are implemented as objects or records with fields for the operator and operands.
This representation has four fields namely, op, arg1, arg2, and result.
op contains an internal code for the operator e.g a three-address instruction x = y + z is represented by placing + in op, y in arg1, z in arg2 and x in result.
However there are exceptions to this;

• Instructions with unary operators like x = minus y or x = y don't use arg2. For a copy statement like x = y, op is = while for other operations, the assignment operator is implied.
• Operators like param neither uses arg2 nor result.
• Conditional and unconditional jumps put the target label in result.

An example
Given the assignment a = b * -c + b * -c;

The translation into three-address code is as follows;

t1 = minus c
t2 = b * t1
t3 = minus c
t4 = b * t3
t5 = t2 + t4
a = t5

The special operator minus is used to distinguish the unary minus operator as in -c from the binary minus operator as in b-c.
The unary minus has two addresses and does the copy statement a = t5.

The implementation of the above three-address code.

#	op	arg1	arg2	result
0	minus	c		t1
1	*	b	t1	t2
2	minus	c		t3
3	*	b	t3	t4
4	+	t2	t4	t5
5	=	t5		a

Identifiers a, b, c are used in the fields arg1, arg2, arg3 instead of pointers to their symbolic-table entries.
Temporary names can be either be entered into the symbol tables like programmer defined names or implemented as objects of class temp with its own methods.

An implementation using triples.

A triple three-address implementation will have three fields namely, op, arg1 and arg2. Unlike quadruples where the result field is used for temporary names, in triples we refer to the result of an operation x op y by its position. Therefore instead of a temporary t1 in the above table, we would refer to position 0.

An example
Given the statement a = b * -c + b * -c;

Its syntax tree is as follows;

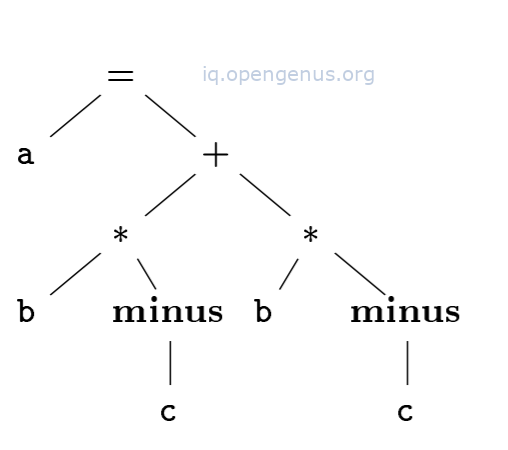
The triple structure is as follows;

#	op	arg1	arg2
0	minus	c
1	*	b	(0)
2	minus	c
3	*	b	(2)
4	+	(1)	(3)
5	=	a	(4)

The copy statement a = t5 is encoded in the triple representation by placing a in the arg1 field and (4) in the arg2 field.

An advantage of quadruples over triples can be seen in an optimizing compiler whereby instructions are moved around. For quadruples if we move an instruction that computes a temporary t, instructions using t don't change. With triples moving an instruction requires changing of all references to that result.
This is solved by indirect triples which consist of a list of pointers to triples.

An example
If we use an array instruction to list pointers to triples, triples from the above table will be represented as follows,

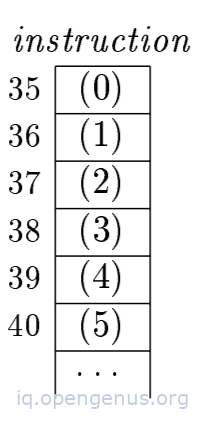
An thus an optimizing compiler can move an instruction by reordering the instruction list without affecting the triples.

Static single assignment (SSA) form.

SSA distinguishes itself from three-address code, firstly, all assignments are to variables with distinct names hence the name static single assignment.

An example
Given the three-address code,

p = a + b
q = p - c
p = q * d
p = e - p
q = p + q

Its SSA form is as follows,

p1 = a + b
q1 = p1 - c
p2 = q1 * d
p3 = e - p2
q2 = p3 + q1

The same variable may be defined in two different control-flow paths e.g
if(flag) x = -1; else x = 1;
y = x * a;
has two control-flow paths where variable x is defined. Therefore, if we use different names for x in the true part and false part of the statement, which assignment should be used in the second assignment?

The second distinction aspect of SSA is that it uses a notational convention called the $\varnothing$-function to combine two definitions of x. i.e
if ( flag ) x1 = -1; else x2 = 1;
x3 = $\varnothing$(x1; x2);

$\varnothing$(x1, x2) has the value x1 if the control flow passes through the true part of the conditional and the value x2 is the control passes through the false part.
We conclude that the $\varnothing$ function returns the value of its arguments corresponding to the control-flow path taken to get to the assignment statement containing the $\varnothing$-function.

Summary.

Three address code is generated by a compiler for code optimization.
It uses a maximum of three addresses to represent any statement.
Three-address code is built upon addresses and instructions.
In object oriented terms, addresses correspond to classes and instructions to the appropriate subclasses.
Three-address code can be implemented by records with fields for the addresses, we have discussed triples, and quadruples for such.

References.

1. Compilers Principles, Techniques, & Tools, Alfred V. Aho, Monica S. Lam.
2. Three-address code generation