
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have presented 2 different approaches to implement 2 Queue Data Structure using a single Array Data Structure.
Table of content
- Definitions
- Algorithm
2.1. Method 1
2.2. Method 2: Optimized - Time & Space complexity
- A way of implementation
1. Definitions
Standard Containers are objects which stores collections of other objects. They are implemented using template classes so they could accept any kind of data type and they need a way to manage the space allocated for them and a way to access them, directly using an index, or through iterators which represent reference objects with similar properties of pointers.
Ex. deque, list
Any container should implement at least these functions:
- empty
- size
- front
- back
- push_back
- pop_front
Queues are containers adaptors based on FIFO (Firs In First Out) rule of accessing elements, meaning we insert elements at one head and remove them from the other head. They are dynamic in size.
template <class T, class Container = deque<T> > class queue;

Containers adaptors are based on standard containers to access their members through them, meaning they encapsulate a standard container called the underlying container and implement its methods.
Arrays are standard containers that uses a strict linear sequence to access their elements, so they are also called sequence containers. The size of them is given as a template parameter and it is allocated at compilation, so they are fixed in size.
template < class T, size_t N > class array;
Note: Do not confuse them with the ordinary arrays used when you declare it with [].
There are major differences between arrays objects and ordinary arrays since arrays are user defined objects with a totally different declaration syntax, structure representation and member functions whilst ordinary arrays are simple a storage of elements (of any type, standard or user defined) in a sequence.
Ex. of declarations:
array<int,3> a1 = {1,2,3}; //array container
int a2[3] = {1,2,3}; //ordinary array
For simplicity of this article we are going to use the ordinary arrays.
2. Algorithm
As we could see from definitions, arrays are fixed and queues are dynamic in size, so we must find a way to split the array in such away that both queues will share the same space keeping the FIFO rule.
Method 1
The common approach is to split the array into 2 halves, and use the indexes to manipulate elements inside the queues.

This method it is useful if you have more than 2 queues, for k queues you might split the array into k parts.
push pseudo code
push(element)
if array[headQueue] is empty
array[headQueue] <- elem;
headQueue <- headQueue - 1
else Queue is full
pop pseudo code
pop()
if ( array[headQueue] is not empty )
temp = array[headQueue] ;
for each element on the left side of array[queueSize]
move all the elements to the right with 1 position
else Queue is empty
return temp;
Method 2: Optimized
As you might already thought you can store elements from the both queues by using the starting point of the both heads of the array and not count the size of them. As long as there is space in the array fill in the elements from one stack or another, so they might not be equal in length as the previous method.

Since the array has only 2 heads, this method can be applied only for 2 queues.
push pseudo code
push(element)
if array[headQueue] is empty
array[headQueue] <- elem;
headQueue <- headQueue + 1
else Queue is full
pop pseudo code
pop()
if ( array[0] is not empty )
temp = array[0] ;
for each element in array
move all the elements to the right (or left) with 1 position
else Queue is empty
return temp;
3. Time & Space complexity
Method 1
push method has O(1) complexity in time and O(n) in space.
pop method has O(n) complexity in time and space.
Method 2
push method has O(1) complexity in time and O(n) in space.
pop method has O(n) complexity in time in space.
4. A way of implementation
Method 1
#include <iostream>
using namespace std;
class Queue2Array
{
private:
int *v, sizeV, idxQ1, idxQ2;
public:
Queue2Array(int size)
{
if (size > 0)
{
v = new int[size];
sizeV = size;
idxQ1 = sizeV / 2 -1;
idxQ2 = sizeV -1;
}
}
void pushQ1(int elem)
{
if (v[idxQ1]==0 && idxQ1 >= 0 )
v[idxQ1--] = elem;
//else Queue 1 is full
}
int popQ1()
{
int temp;
if ( v[sizeV / 2 -1] )
{
temp = v[sizeV / 2 -1] ;
for (int i=sizeV / 2 -1; i > 0 ;i--) //move all the elements to the right
{
v[i] = v[i-1];
v[i-1] = 0;
}
}
//else Queue 1 is empty
return temp;
}
void pushQ2(int elem)
{
if (v[idxQ2]==0 && idxQ2 >= sizeV/2 )
v[idxQ2--] = elem;
//else Queue 2 is full
}
int popQ2()
{
int temp;
if ( v[sizeV-1] )
{
temp = v[sizeV-1] ;
for (int i=sizeV-1; i > sizeV/2 ;i--) //move all the elements to the right
{
v[i] = v[i-1];
v[i-1] = 0;
}
}
//else Queue 2 is empty
return temp;
}
void coutV()
{
for (int i=0;i<sizeV;i++)
cout<<"v["<<i<<"]="<<v[i]<<endl;
}
};
int main()
{
Queue2Array a(5);
a.pushQ1(11);
a.pushQ1(12);
a.pushQ1(13);
a.pushQ2(21);
a.pushQ2(22);
a.pushQ2(23);
a.coutV();
cout<<a.popQ1()<<endl;
a.coutV();
cout<<a.popQ1()<<endl;
a.coutV();
cout<<a.popQ1()<<endl;
a.coutV();
cout<<a.popQ2()<<endl;
a.coutV();
cout<<a.popQ2()<<endl;
a.coutV();
cout<<a.popQ2()<<endl;
a.coutV();
return 0;
}
Step by step example
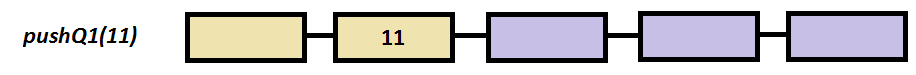
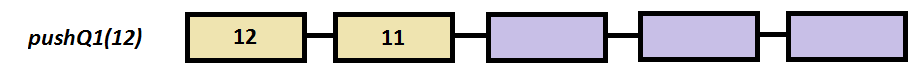
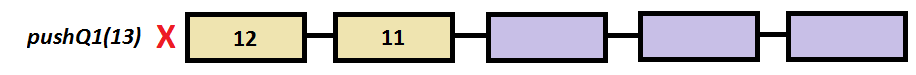
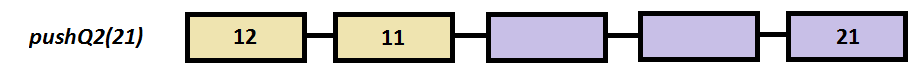
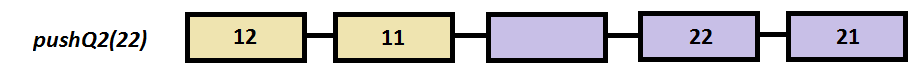
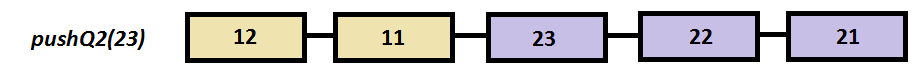
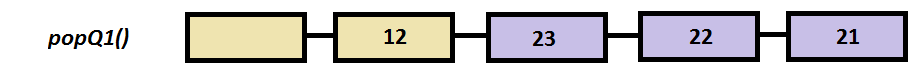
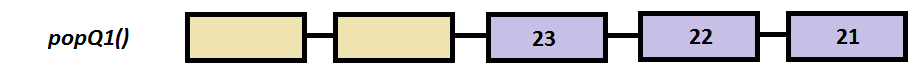
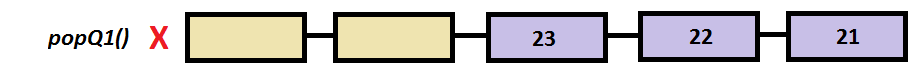
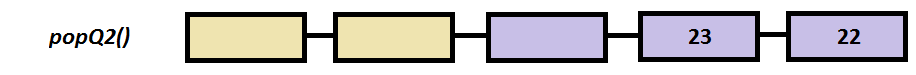
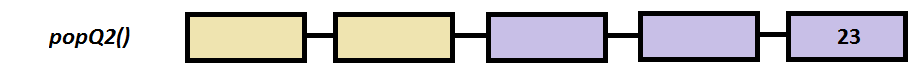
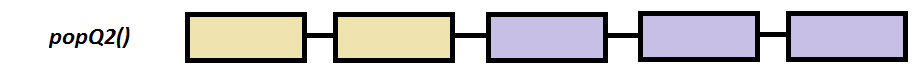
Method 2
#include <iostream>
using namespace std;
class Queue2Array
{
private:
int *v, sizeV, idxQ1, idxQ2;
public:
Queue2Array(int size)
{
if (size > 0)
{
v = new int[size];
sizeV = size;
idxQ1 = 0;
idxQ2 = sizeV -1;
}
}
void pushQ1(int elem)
{
if (v[idxQ1]==0 && idxQ1 <= idxQ2 )
v[idxQ1++] = elem;
//else Queue 1 is full
}
int popQ1()
{
int temp;
if ( v[0] )
{
temp = v[0] ;
if(idxQ1 > 1)
for (int i=0; i+1 < idxQ1 ;i++) //move all the elements to the left
{
v[i] = v[i+1];
v[i+1] = 0;
}
else
v[0] = 0;
idxQ1--;
}
//else Queue 1 is empty
return temp;
}
void pushQ2(int elem)
{
if (v[idxQ2]==0 && idxQ2 >= idxQ1 )
v[idxQ2--] = elem;
//else Queue 2 is full
}
int popQ2()
{
int temp;
if ( v[sizeV-1] )
{
temp = v[sizeV-1] ;
if(idxQ2 < sizeV-2)
for (int i=sizeV-1; i-1 > idxQ2 ;i--) //move all the elements to the right
{
v[i] = v[i-1];
v[i-1] = 0;
}
else
v[sizeV-1] = 0;
idxQ2++;
}
//else Queue 2 is empty
return temp;
}
void coutV()
{
for (int i=0;i<sizeV;i++)
cout<<"v["<<i<<"]="<<v[i]<<endl;
}
};
int main()
{
Queue2Array a(5);
a.pushQ1(11);
a.pushQ1(12);
a.pushQ1(13);
a.pushQ2(21);
a.pushQ2(22);
a.pushQ2(23);
a.coutV();
cout<<a.popQ1()<<endl;
a.coutV();
a.pushQ2(23);
a.coutV();
return 0;
}
Step by step example

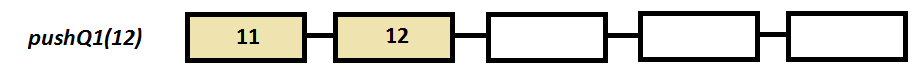
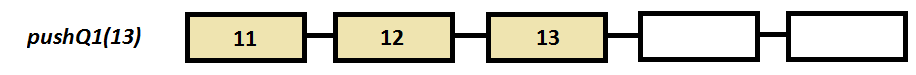
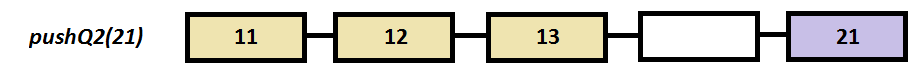
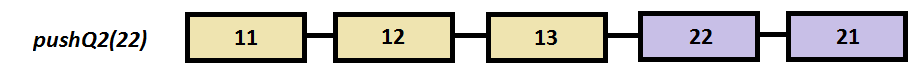
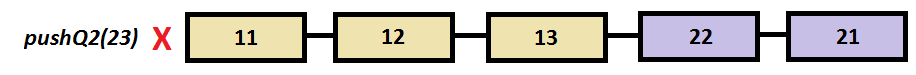
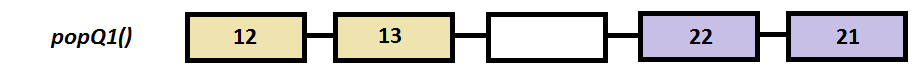
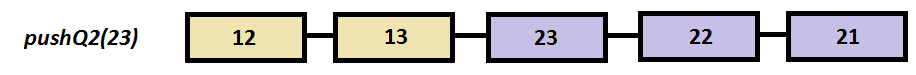
With this article at OpenGenus, you must have the complete idea of how to implement 2 Queues in a single Array.
