
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this article, we have explored the Car Pooling Problem in depth and presented an efficient approach to solve it using the concept of Prefix Sum.
Table of contents:
- Problem Statement
- Constraints
- Example Test Cases
- Explanation of Example 1
- Prefix Sum
- Algorithm for Car pooling problem
- Code for Car pooling Problem
- Code Explanation
- Time Complexity
- Space Complexity
- Another Approach: Complexity O(N^2)
- Conclusion
Problem Statement:
There is a car with capacity empty seats. The vehicle only drives east (i.e., it cannot turn around and drive west).
You are given the integer capacity and an array trips where trips[i] = [numPassengersi, fromi, toi] indicates that the ith trip has numPassengersi passengers and the locations to pick them up and drop them off are fromi and toi respectively. The locations are given as the number of kilometers due east from the car's initial location.
Return true if it is possible to pick up and drop off all passengers for all the given trips, or false otherwise.
Constraints
- 1 <= trips.length <= 1000
- trips[i].length == 3
- 1 <= numPassengersi <= 100
- 0 <= fromi < toi <= 1000
- 1 <= capacity <= 10^5
Example Test Cases
- Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: true - Input: trips = [[2,1,5],[3,3,7]], capacity = 4
Output: false
Explanation of Example 1
In this case the car is moving only in one direction that is east and we have to check that whether the passengers that we pick and drop at any index are less than or equal to the capacity mentioned.

This is the initial condition where car is at the index=0 and no. Of passengers=0.

Now car moves to index one and two passengers enter into it.

Car moves to index 2
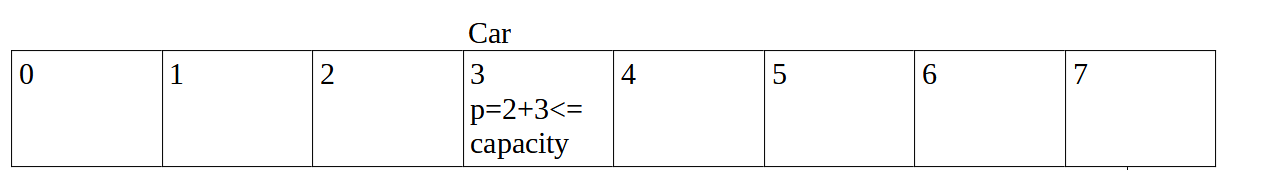
Now car moves to index =3 and 3 additional people enter into it but p<=capacity so it is valid.

Car moves to index 4 with total passengers 5.

At index=5 , 2 passengers drop off which sat in the car at index 1

Now car moves to index = 6

At last at index 7 all the remaining passengers drop off from the car and p=0.
Similarly when we analyse example 2 we can see that the capacity mentioned is 4 but at index = 3 the value of p becomes 5 so it means the trip is not valid and the answer is false.
So, the concept that can be used in this problem is prefix sum or cumulative sum.
Prefix Sum
To understand this concept let us consider an array = [3, -1, 4, -3, 5, 7]
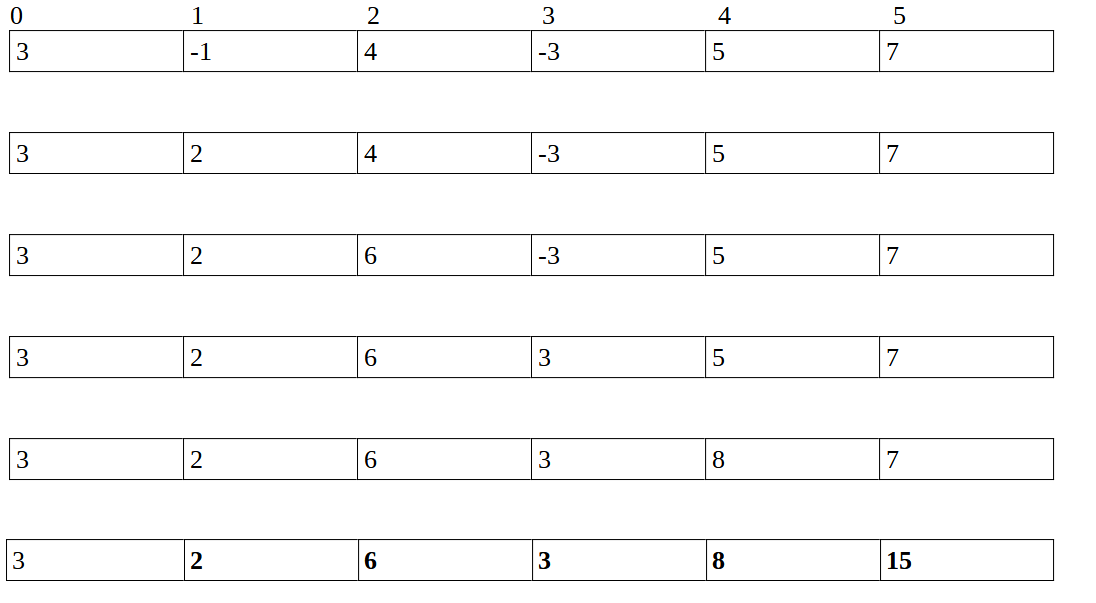
So in each step you can see if we want to calculate the prefix array then the
arr[i]= arr[i] + arr[i-1]
So if you want to calculate for complete array then its pseudocode is
for (i=0 to n-1 ; i++)
{
arr[i] = arr[i] + arr[i-1]
}
So to calculate the sum between range [i, j]
we have:
arr[i,j] = arr[j] – arr[i-1]
Algorithm for Car pooling problem
- Initiate vector of vector named as trips.
- Finaldrop=-1;
3. for(trip[] from trips[][])
maximum of(finaldrop, drop index of each trip)
- Initiate prefixsum array and insert values in it
for(vector<int>trip: trips){
prefixsum[trip[1]]+=trip[0];
prefixsum[trip[2]]-=trip[0];
}
- Perform cumulative sum on the prefix sum array and check the addition at each index with the capacity and if it greater then print false and it will exit the loop and print true.
Code for Car pooling Problem
#include<bits/stdc++.h>
using namespace std;
int main(){
vector<vector<int>> trips={{2,1,5},
{3,3,7}};
int capacity=5;
int finaldrop=-1;
for(vector<int>trip: trips){
finaldrop= max(finaldrop, trip[2]);
}
vector<int>prefixsum(finaldrop+1, 0);
for(vector<int>trip: trips){
prefixsum[trip[1]]+=trip[0];
prefixsum[trip[2]]-=trip[0];
}
for(int i=0; i<finaldrop; i++){
prefixsum[i+1]+=prefixsum[i];
if(prefixsum[i]>capacity){
cout<<"False"<<endl;
return 0;
}
}
cout<<"True"<<endl;
return 0;
}
Input: trips = [[2,1,5],[3,3,7]], capacity = 5
Output: True
Code Explanation:
- Declare a integer variable finaldrop =-1 to calculate the final dropping index.
- Traverse each vector and compare the drop indexes of each trip using max function.
- Initiate the vector prefixsum to store the prefix sum array.
- Now make the vector prefixsum of size finaldrop+1 and make all values of that vector to zero.
- Traverse the trips and add number of passengers at that particular index and write the negative of that number of passengers if they are dropping off.
Eg:

Prefixsum array (initially)

Prefixsum array(after traversing the trips)

-
Traverse the prefixsum array and perform prefix sum or cumulative sum on it so that the array becomes:

-
And simultaneously check whether the any index of the prefixsum array is greater that the capacity and if it is then return false or else then it will come out of the loop and and return true which means the trip was possible.
Time Complexity:
Time Complexity of this approach would be O(n) as the first loop would run of O(n) then the next both loops of prefix sum would run for O(n) times as well. We could even consider the last loop as of constant time complexity because the maximum drop index can be 1000 and not more than that and so for that we can even declare the array of 1001. But in this case we have not declared that and used vectors instead.
So, the time complexity is O(n).
Space Complexity
In this we have used vector as an array so the space complexity for it would be O(n)
Another Approach: Complexity O(N^2)
In this, first iterate over the sub-trips and then in the inner loop
iterate over the start and endpoint of the trip and add the value of the number of passengers to the element of the array of that index.
for(int i=0;i<trips.size();i++){
for(int j=trips[i][1];j<trips[i][2];j++){
arr[j]+=trips[i][0];
if(arr[j]>capacity){
cout<<" false"<<endl;
return 0;
}
}
}
cout<<"True"<<endl;
Here there are nested for loops so the time complexity is O(n^2).
Conclusion
This article at OpenGenus focused on solving car pooling problem and understanding the concept of prefix sum array which was required to solve this problem.
