
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Table of contents:
- Arithmetic coding (Encoding)
- Arithmetic coding (Decoding)
- Example (Encoding)
- Example (Decoding)
- Implementation (encoding and decoding)
- Time Complexity
- Application
- Question
Arithmetic coding (Encoding)
Arithmetic coding is a sophisticated method to compress data based on the probability of occurrence of each unique symbol in a message.
To encode a message, we can do as follows:
Step 1: Calculate the frequency of occurrences of each unique character/ symbol in the message. Then use the frequency to generate the probability of occurrence for each unique character/ symbol
Step 2: The initial entire range will be
[0, 1)
Calculate the cumulative sum using the probability of occurrence calculated in step 1 and assign each unique character/symbol to an interval of probabilities. (see encoding example - step 2)
Step 3: For each character/ symbol in the message, we narrow down the entire interval based on the upper bound and lower bound of the interval of probabilities of that character. Calculate a new cumulative sum and assign each unique character/symbol to a range in the new interval. (see encoding example - step 3)
Step 4: Calculate the tag:
tag = (upper_bound_of_last_char_range + lower_bound_of_last_char_range)/2
Arithmetic coding (Decoding)
Assume that we have a tag, the coding model (probability of occurrence of each character/ symbol in the message), and the length of the message.
We will iteratively narrow down the entire interval until the number of iterations equals the length of the message. For each iteration, we will narrow down the entire interval based on the tag. We choose the sub-interval that contains the tag to be the new entire interval. The message is the character/ symbol that has its interval chosen to be the new entire interval during each iteration. (see decoding example)
Example (Encoding)
Assume that we want to encode the message "OpenGenus" using arithmetic coding.
The length of the message is 9 (i.e. the message has 9 characters). The unique characters are 'O', 'p', 'e', 'n', 'G', 'u', 's'.
Step 1: Generate the probability of occurrence of each unique character.
The table below shows the frequency of occurrences of each unique character in the message "OpenGenus", then use it to calculate the probability of occurrence of each unique character:
| Character | Frequency | Probability |
|---|---|---|
| 'O' | 1 | 1/9 = 0.1111111111111111 |
| 'p' | 1 | 1/9 = 0.1111111111111111 |
| 'e' | 2 | 2/9 = 0.2222222222222222 |
| 'n' | 2 | 2/9 = 0.2222222222222222 |
| 'G' | 1 | 1/9 = 0.1111111111111111 |
| 'u' | 1 | 1/9 = 0.1111111111111111 |
| 's' | 1 | 1/9 = 0.1111111111111111 |
Step 2: The initial interval for each character in the message is as follows:
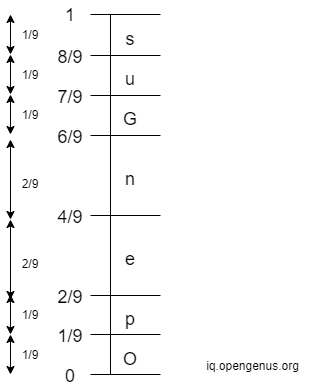
Step 3: Iterate through the whole message 'OpenGenus'. For each character in the message, we narrow down the entire range based on the upper bound and lower bound of the interval of that character. The initial entire interval is
[0, 1)
After the entire interval is narrowed down, find the new range of probabilities of each unique character in the new entire interval. See the demonstration below:
- 1st Iteration: The 1st character in 'OpenGenus' is 'O'. The interval of 'O' is
[0, 1/9)
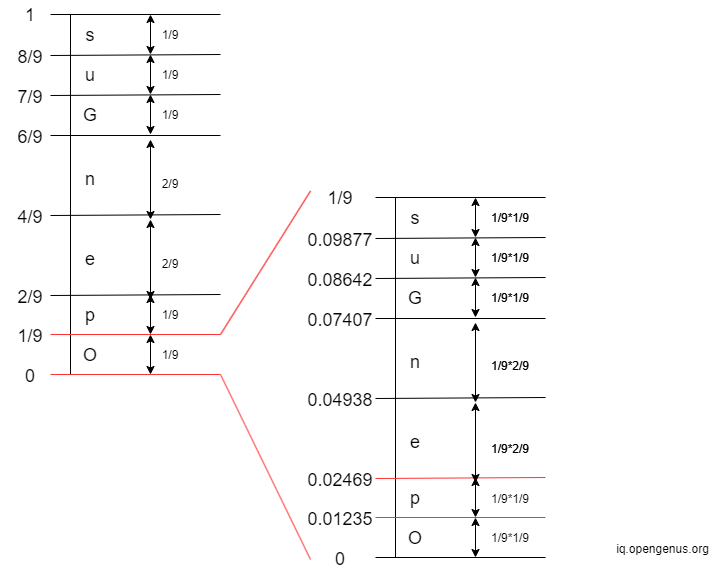
- 2nd Iteration: The 2nd character in 'OpenGenus' is 'p'. The interval of 'p' is
[0.01235, 0.02469)
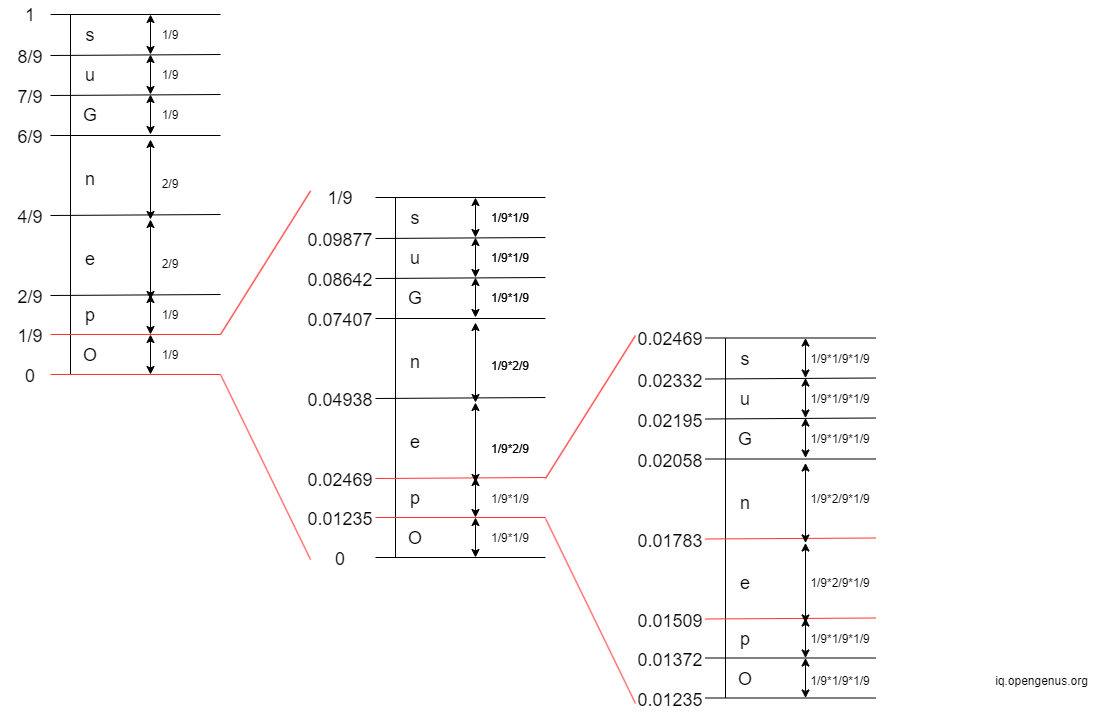
- 3rd Iteration: The 3rd character in 'OpenGenus' is 'e'. The interval of 'e' is
[0.01509, 0.01783)
- 4th Iteration: The 4th character in 'OpenGenus' is 'n'. The interval of 'n' is
[0.01631, 0.01692)
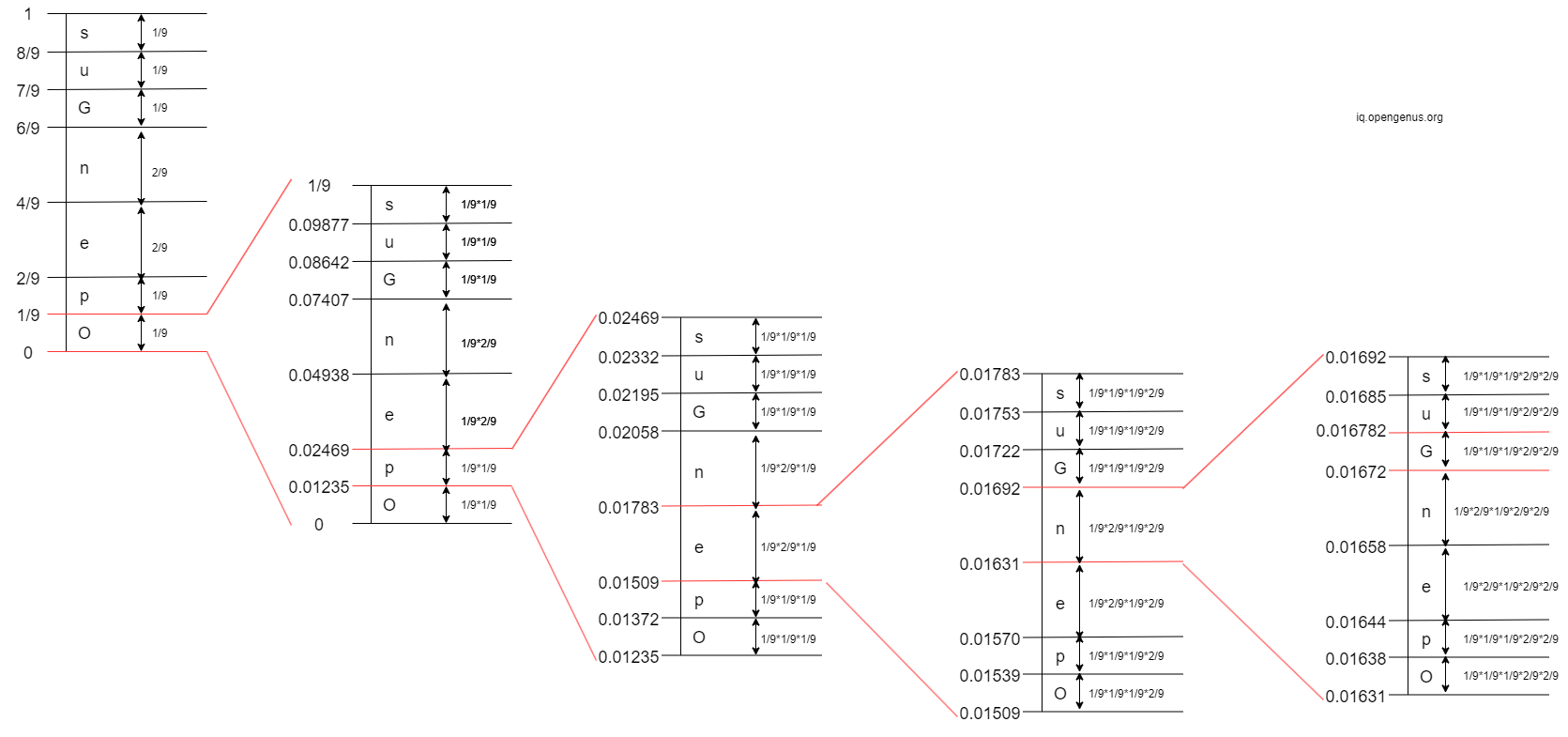
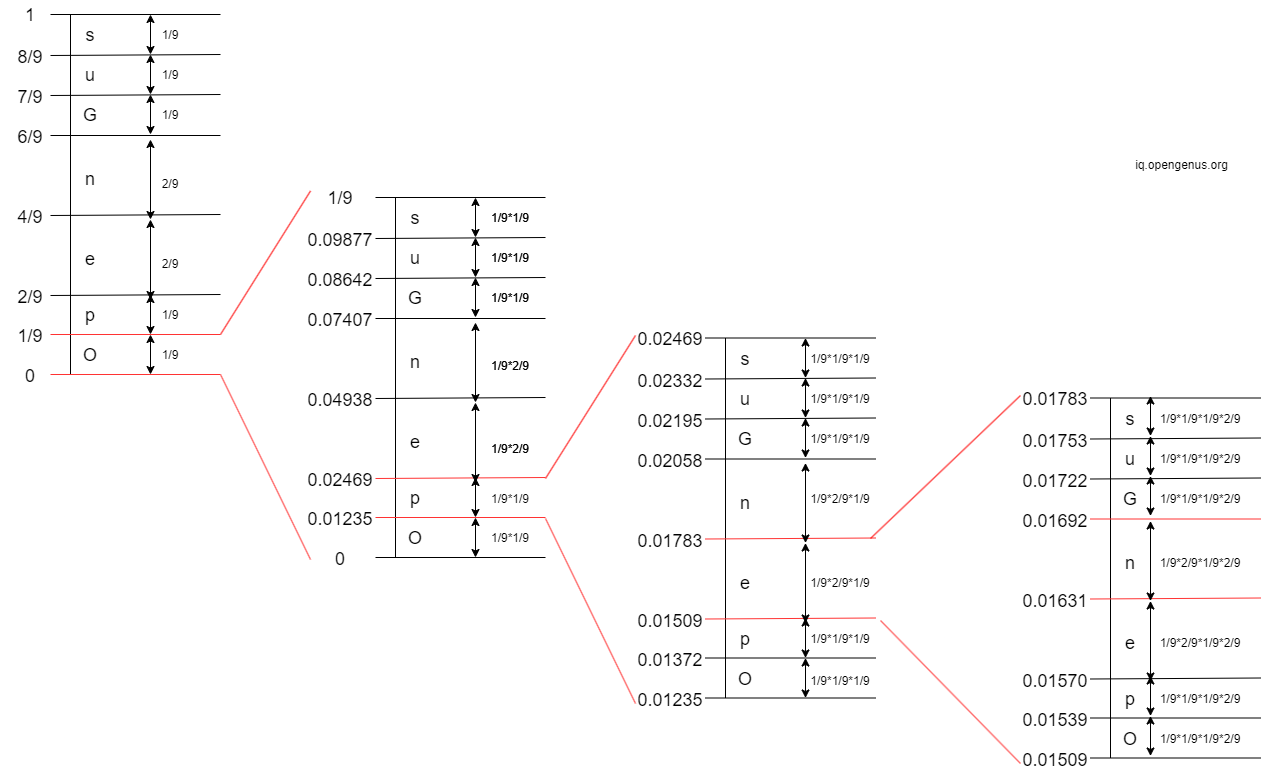
- 5th Iteration: The 5th character in 'OpenGenus' is 'G'. The interval of 'G' is
[0.01672, 0.016782)
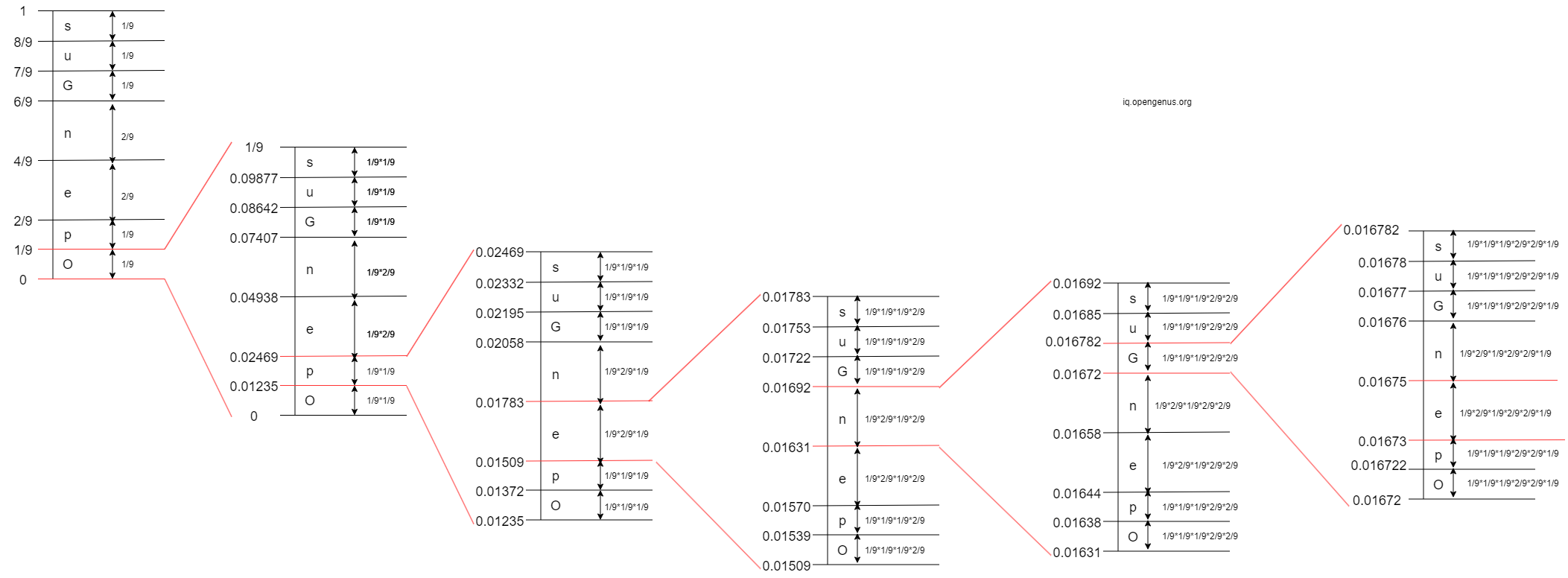
- 6th Iteration: The 6th character in 'OpenGenus' is 'e'. The interval of 'e' is
[0.01673, 0.01675)
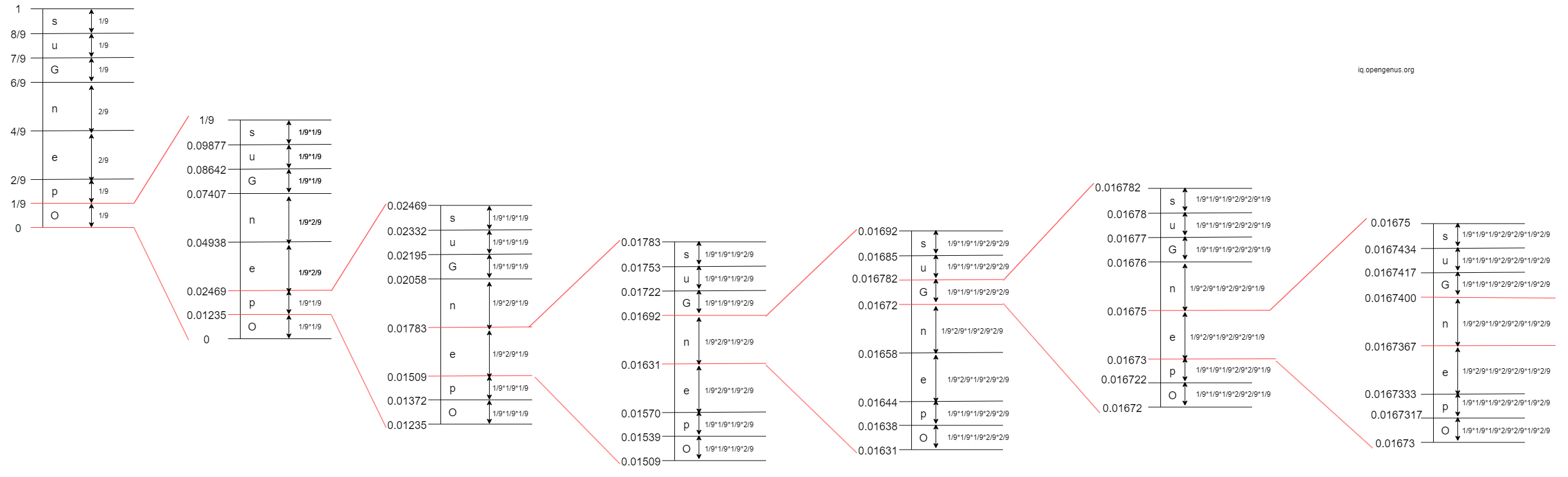
- 7th Iteration: The 7th character in 'OpenGenus' is 'n'. The interval of 'n' is
[0.0167367, 0.0167400)
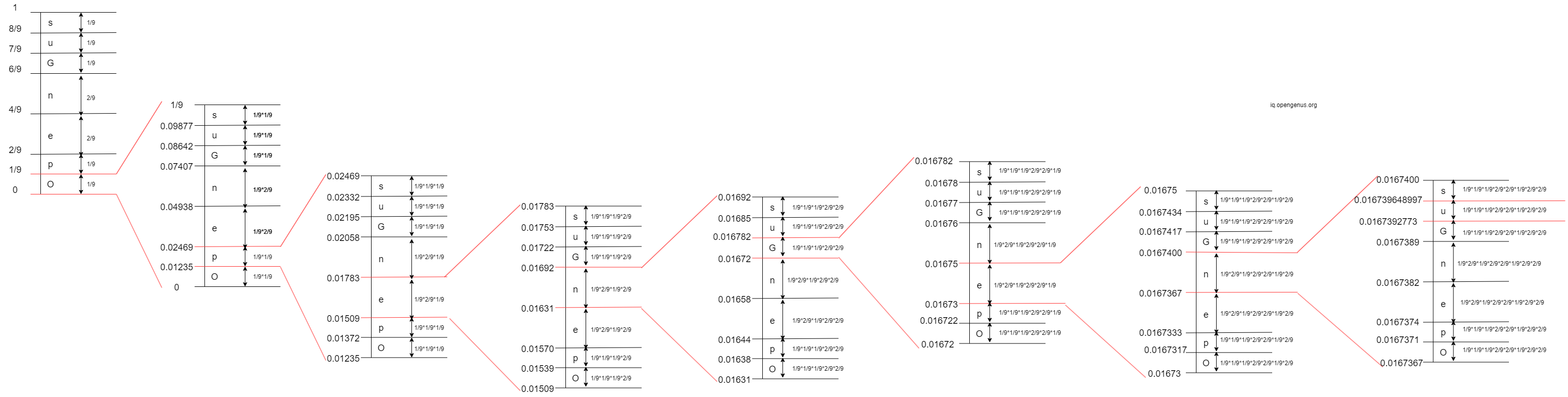
- 8th Iteration: The 8th character in 'OpenGenus' is 'u'. The interval of 'u' is
[0.0167392773, 0.016739648997)
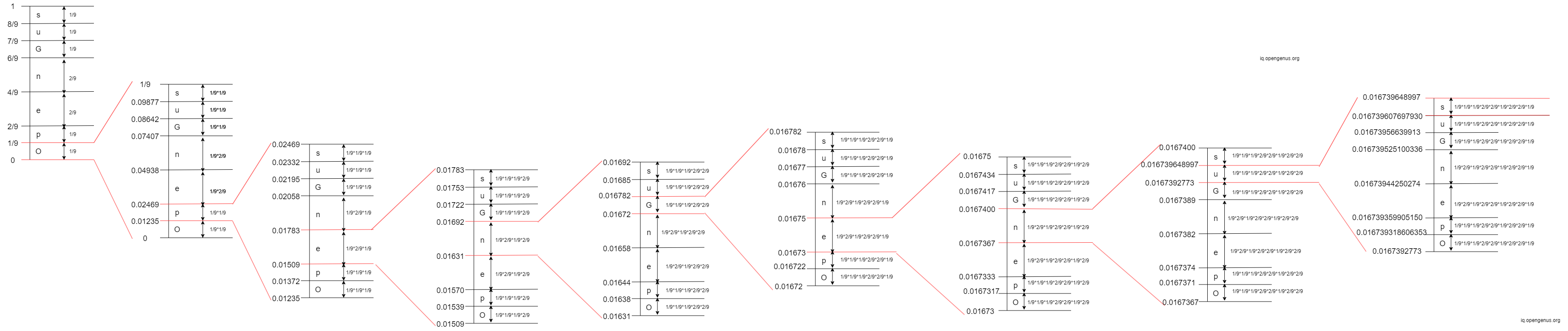
- 9th Iteration: The 9th character in 'OpenGenus' is 's'. The interval of 's' is
[0.016739607697930, 0.016739648997)

Step 4: Calculate the tag:
tag = (0.016739648997 + 0.016739607697930)/2 = approximately 0.016739628347
Example (Decoding)
Assume that we want to decode the tag from the previous example about encoding
tag = 0.016739628347
The length of the message is 9 (i.e. the message has 9 characters).
The probability of each character is as follows:
{'O': 0.1111111111111111, 'p': 0.1111111111111111, 'e': 0.2222222222222222, 'n': 0.2222222222222222, 'G': 0.1111111111111111, 'u': 0.1111111111111111, 's': 0.1111111111111111}
Since the length of the message is 9, there are 9 iterations.
- 1st Iteration: 0 < tag = 0.016739628347 < 1/9 => 1st character is 'O'

- 2nd Iteration: 0.01235 < tag = 0.016739628347 < 0.02469 => 2nd character is 'p'

- 3rd Iteration: 0.01509 < tag = 0.016739628347 < 0.01783 => 3rd character is 'e'

- 4th Iteration: 0.01631 < tag = 0.016739628347 < 0.01692 => 4th character is 'n'

- 5th Iteration: 0.01672 < tag = 0.016739628347 < 0.016782 => 5th character is 'G'

- 6th Iteration: 0.01673 < tag = 0.016739628347 < 0.01675 => 6th character is 'e'

- 7th Iteration: 0.0167367 < tag = 0.016739628347 < 0.0167400 => 7th character is 'n'

- 8th Iteration: 0.0167392773 < tag = 0.016739628347 < 0.016739648997 => 8th character is 'u'

- 9th Iteration: 0.016739607697930 < tag = 0.016739628347 < 0.016739648997 => 9th character is 's'

Implementation (encoding and decoding)
Python implementation for arithmetic encoding and decoding:
def get_unique_char(message): # O(n^2)
unique_char = []
for character in message: # O(n)
unique = True
# check if the character has already been added to unique_char list
for e in unique_char: # O(n)
if e == character:
# change unique to False if the character already exist in unique_char list
unique = False
break
if unique:
unique_char.append(character) # O(1) amortized
return unique_char
def get_frequency(message, unique_char): # O(n^2)
# use a dictionary where
# the key is the unique character
# the value is the frequency
frequency = {}
for character in unique_char: # O(n)
char_freq = 0
# count the number of occurrences of the current character
for e in message: # O(n)
if character == e:
# increase char_freq by 1 every time a character in message
# is the same as a character in the unique_char list
char_freq += 1
frequency[character] = char_freq # Average case O(1) or Amortized worst case O(n)
return frequency
def get_occurring_probability(message, frequency): # O(n)
# use a dictionary where
# the key is the unique character
# the value is the probability of occurrence
probability = {}
message_length = len(message)
for key, value in frequency.items(): # O(n)
# probability of occurrence of a unique character = frequency/message_length
probability[key] = value / message_length
return probability
def get_cumulative_sum(lower_bound, upper_bound, probability_ls): # O(n) (where append to a list takes O(1) amortized)
cumulative_sum = [lower_bound]
diff_btw_two_bounds = upper_bound - lower_bound
char_lower_bound = lower_bound
for probability in probability_ls: # O(n)
char_upper_bound = char_lower_bound + (diff_btw_two_bounds * probability)
cumulative_sum.append(char_upper_bound) # O(1) amortized
char_lower_bound = char_upper_bound
return cumulative_sum
def associate_key_with_interval(cumulative_sum, unique_char): # O(n) (where adding to a dictionary O(1) average case)
# use a dictionary where
# the key is the unique character
# the value is a list of length 2 where
# - the first element is the lower bound
# - the second element is the upper bound
interval = {}
i = 0
j = 0
while i < len(cumulative_sum) - 1: # O(n)
key = unique_char[j]
lower_bound = cumulative_sum[i]
upper_bound = cumulative_sum[i + 1]
interval[key] = [lower_bound, upper_bound] # Average case O(1) or Amortized worst case O(n)
i += 1
j += 1
return interval
# get_tag() takes O(n^2) (if get_cumulative_sum() and associate_key_with_interval() take O(n))
def get_tag(probability, unique_char, message):
# put all values from probability dictionary into a probability list
probability_ls = []
for key, value in probability.items(): # O(n)
probability_ls.append(value) # O(1) amortized
# then use the probability list to calculate cumulative sum of probability_ls
# initially, the lower bound is 0.0 and the upper bound is 1.0
cumulative_sum = get_cumulative_sum(0.0, 1.0, probability_ls) # O(n) (where append to a list takes O(1) amortized)
print('Cumulative sum for interval [0, 1): ', cumulative_sum)
# associate each key with its interval
interval_dict = associate_key_with_interval(cumulative_sum,
unique_char) # O(n) (where adding to a dictionary O(1) average case)
# get the tag
tag = 0.0
for character in message: # O(n)
# get the interval of the current character (narrow down the interval)
char_interval = interval_dict.get(character) # Average case O(1) or Amortized worst case O(n)
# get the lower and upper bound of the interval of the current character
char_lower_bound = char_interval[0]
char_upper_bound = char_interval[1]
# calculate the tag: tag = average of lower and upper bound
# the tag is recalculated until the last element in the message is reached
tag = (char_lower_bound + char_upper_bound) / 2.0
# every time the interval is narrowed down:
# - get the new cumulative sum for the new interval
# - each key will have a new lower and upper bound in the new interval
cumulative_sum = get_cumulative_sum(char_lower_bound, char_upper_bound,
probability_ls) # O(n) (where append to a list takes O(1)
interval_dict = associate_key_with_interval(cumulative_sum,
unique_char) # O(n) (where adding to a dictionary O(1) average case)
return tag
def concatenate_char(ls): # O(n)
string = ''
for e in ls: # O(n)
string += e
return string
def arithmetic_encoding(message): # O(n^2)
# generate a list that contains unique characters in the message
unique_char = get_unique_char(message) # O(n^2)
print('Unique char in the message: ', unique_char)
# get frequency of occurrences of all unique characters in the message
frequency = get_frequency(message, unique_char) # O(n^2)
print('Frequency of each unique character: ', frequency)
# get probability of occurrence of all unique characters in the message
probability = get_occurring_probability(message, frequency) # O(n)
print('Occurring probability of each unique character: ', probability)
# get the tag: get_tag() takes O(n^2) (if get_cumulative_sum() and associate_key_with_interval() take O(n))
tag = get_tag(probability, unique_char, message) # O(n^2)
return tag, probability
def arithmetic_decoding(probability, message_length, tag): # O(n^2)
# put all values from probability dictionary into a probability list
# put all keys from probability dictionary into a unique_char list
probability_ls = []
unique_char = []
for key, value in probability.items(): # O(n)
probability_ls.append(value) # O(1) amortized
unique_char.append(key) # O(1) amortized
# then use the probability list to calculate cumulative sum of probability_ls
# initially, the lower bound is 0.0 and the upper bound is 1.0
cumulative_sum = get_cumulative_sum(0.0, 1.0, probability_ls) # O(n) (where append to a list takes O(1) amortized)
# associate each key with its interval
interval_dict = associate_key_with_interval(cumulative_sum,
unique_char) # O(n) (where adding to a dictionary O(1) average case)
i = 0
message_char_ls = []
current_lower_bound = 0.0
current_upper_bound = 1.0
while i < message_length: # O(n)
for key, value in interval_dict.items(): # O(n)
# get the interval of the current character (key)
lower_bound = value[0]
upper_bound = value[1]
# check if tag is within the interval of the current character (key)
if (tag > lower_bound) and (tag < upper_bound):
# narrow down the interval
current_lower_bound = lower_bound
current_upper_bound = upper_bound
# add the character to message_char_ls if tag is within the interval of the current character (key)
message_char_ls.append(key) # O(1) amortized
break
# every time the interval is narrowed down:
# - get the new cumulative sum for the new interval
# - each key will have a new lower and upper bound in the new interval
cumulative_sum = get_cumulative_sum(current_lower_bound, current_upper_bound,
probability_ls) # O(n) (where append to a list takes O(1) amortized)
interval_dict = associate_key_with_interval(cumulative_sum,
unique_char) # O(n) (where adding to a dictionary O(1) average case)
i += 1
return concatenate_char(message_char_ls)
def run_arithmetic_coding():
message = 'OpenGenus'
message_len = len(message)
print('The message is ', message)
print('The length of the message is', message_len)
tag, probability = arithmetic_encoding(message)
print('The tag for ', message, ' is ', tag)
decoded_msg = arithmetic_decoding(probability, message_len, tag)
print('Decode the message using probability (coding model), message length, and the generated tag: ', decoded_msg)
if __name__ == '__main__':
run_arithmetic_coding()
If we run the program above for the message 'OpenGenus', we will have the following output:
The message is OpenGenus
The length of the message is 9
Unique char in the message: ['O', 'p', 'e', 'n', 'G', 'u', 's']
Frequency of each unique character: {'O': 1, 'p': 1, 'e': 2, 'n': 2, 'G': 1, 'u': 1, 's': 1}
Occurring probability of each unique character:
{
'O': 0.1111111111111111,
'p': 0.1111111111111111,
'e': 0.2222222222222222,
'n': 0.2222222222222222,
'G': 0.1111111111111111,
'u': 0.1111111111111111,
's': 0.1111111111111111
}
Cumulative sum for interval [0, 1): [0.0, 0.1111111111111111, 0.2222222222222222, 0.4444444444444444, 0.6666666666666666, 0.7777777777777777, 0.8888888888888888, 1.0]
The tag for OpenGenus is 0.016739628347327812
Decode the message using probability (coding model), message length, and the generated tag: OpenGenus
Time Complexity
The time complexity for the above implementation is:
- Encoding:
O(n^2)(see the comment in the Python implementation for detailed analysis) - Decoding:
O(n^2)(see the comment in the Python implementation for detailed analysis)
Application
Arithmetic coding is used for
- data compression (compress files such as JPEG, PNG, etc)
- image or video compression
- text compression
- etc
It helps reduce the size of files that are transmitted through the network and makes the transmission more efficient.
Question
What is the tag for the message "AB"?
