Boundary Fill Algorithm

In the days of MS-Paint, we all drew something and filled it with a color. Such task falls under Region Filling (Seed-Fill) Algorithms.

Region Filling is the process of filling a region or an image. Further depending upon filling, it can be categorized as:

1. Boundary Filling Algorithm - region inside the boundary of same pixel value
2. Flood Filling Algorithm - region having same pixel value

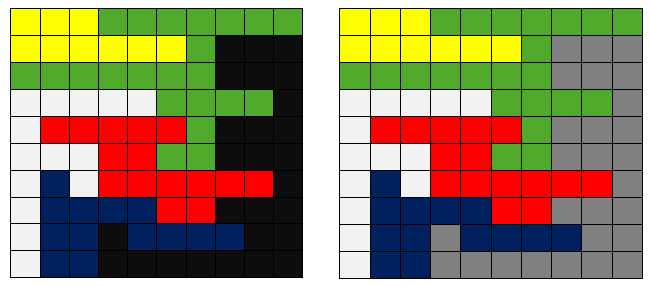
Fig.1 Flood Fill Algorithm

Fig.2 Boundary Fill Algorithm

In this article, we are going to discuss about Boundary Algorithm.

Introduction to Boundary Fill Algorithm

In computer graphics, Boundary Fill algorithm is used to fill a inside of closed polygon having boundary of same color with a desired color. It is mainly used with interactive-painting packages where an inside point can be easily chosen as its approach requires a starting pixel also called seed, to start with.

Details on Implementation and Problem statement

It is mainly implemented using stack-based recursion. Functioning of the boundary-fill requires an interior point (x,y) , fill color and boundary color to start with. The algorithm starts by checking whether a pixel value equals to boundary color or fill color . If not, pixel is filled with desired color and advances to check for neighboring pixels. Else, not. The process continues until it hits all sides of the boundary region.

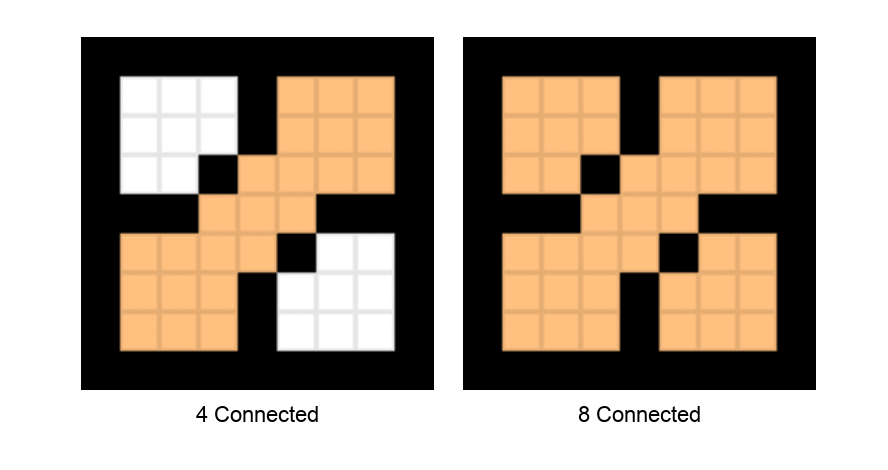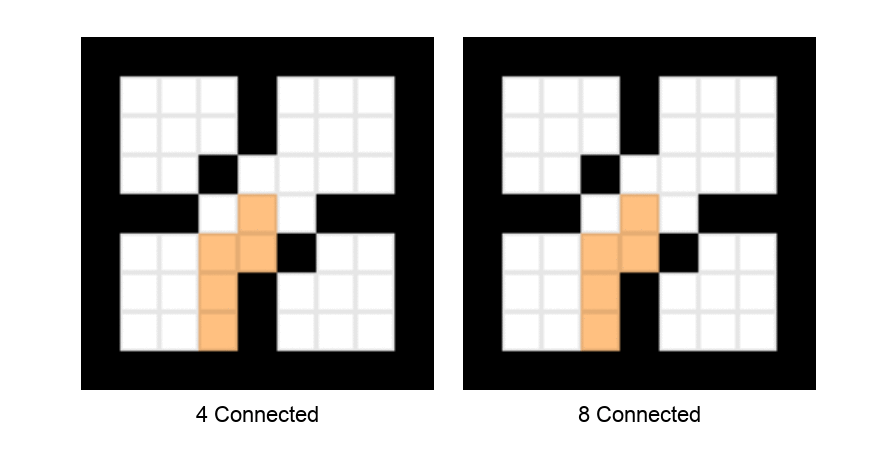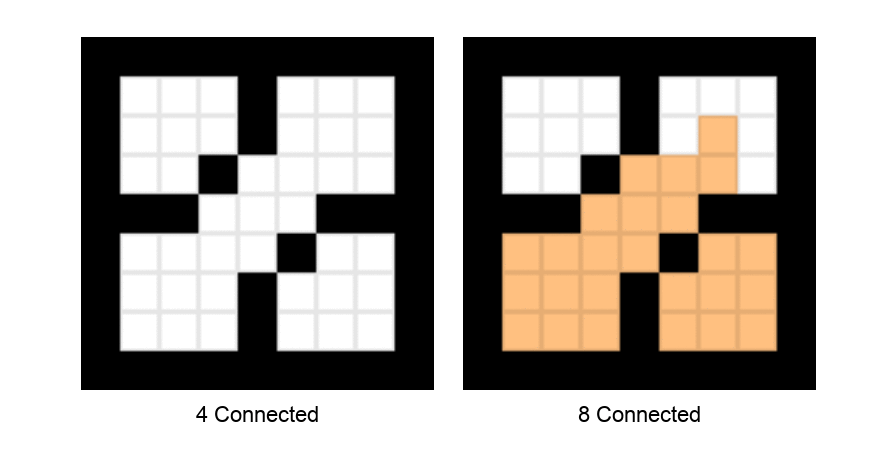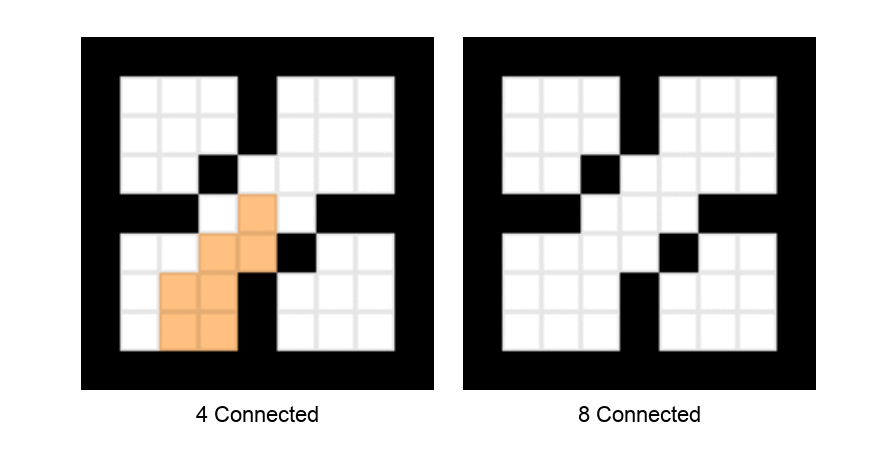
Further, Boundary-fill algorithm can be implemented using 4-connected pixels and 8-connected pixels.
4-connected pixels : Neighboring pixels are pixels on left,right,above and below of current pixel.
8-connected pixels : Neighboring pixels are left,right ,above ,below and 4 diagonal pixels as shown below.

Fig.3 Neighboring Pixels

4-connected vs 8-connected

In case of sharp boundaries, 4-connected method fails, while 8-connected method filled the region efficiently. Following figure represents the situation.

Boundary Fill Algorithm

Steps in Boundary Fill Algorithm:

1. There are two defined colors: color of boundary (color_boundary) and color that needs to be filled (color_fill)
2. Get color (say color1) of the current pixel
3. If color1 is equal to color_boundary or color_fill, nothing needs to be done as correct color is already assigned.
4. If color1 is not equal to the two values:
   4.1. Add color_fill to the current pixel.
   4.2. Do the same process for 4 adjacent pixel points: (x, y-1), (x+1, y), (x, y+1), (x-1, y)
   4.3. If 8-connected fill is being done, do the same process for 4 diagonal pixel points additionally: (x+1, y-1), (x+1, y+1), (x-1, y+1), (x-1, y-1).
5. Do the process for every pixel point.

void boundary_fill(int x,int y,int  fill_color,int boundary_color){
	
	int cur_color = getpixel(x,y);

	if(cur_color == boundary_color or cur_color == fill_color)
		return;

	fillpixel(x,y,fill_color);

	boundary_fill(x,y-1,fill_color,boundary_color);
	boundary_fill(x+1,y,fill_color,boundary_color);
	boundary_fill(x,y+1,fill_color,boundary_color);
	boundary_fill(x-1,y,fill_color,boundary_color);

	/*For 8-connected pixels,additional calls
	boundary_fill(x+1,y-1,fill_color,boundary_color);
	boundary_fill(x+1,y+1,fill_color,boundary_color);
	boundary_fill(x-1,y+1,fill_color,boundary_color);
	boundary_fill(x-1,y-1,fill_color,boundary_color);
	*/
}

The time complexity of Boundary Fill Algorithm is O(N) where N is the number of pixels.

The space complexity is O(N) from the recursive calls. In an iterative implementation, space complexity will be O(1).

Restrictions

1. Starting point should be inside closed polygon.
2. For all edges of a polygon, boundary color should be same.
3. It may fail to fill in case some interior pixels are already filled with color.

With this article at OpenGenus, you must have the complete idea of Boundary Fill Algorithm.