Calculate Binomial Coefficient using Dynamic Programming

Reading time: 30 minutes | Coding time: 10 minutes

Binomial Coefficient is the coefficient in the Binomial Theorem which is an arithmetic expansion. It is denoted as C(N, K) which is equal to N! / (K! * (N-K)!) where ! denotes factorial.

This follows a recursive relation using which we will calculate the N binomial coefficient in linear time O(N * K) using Dynamic Programming.

To know Binomial Coefficient, first we have to know what is Binomial Theorem?

What is Binomial Theorem ?

Binomial Theorem is also called as Binomial Expansion delineat the powers in algebric equations. Binomial Theorem helps us to find the expanded the expanded polynomial without multiplying the bunch of binomials at a time. The expanded polynomial will always contain one more than the power you are expanding.

Following figure shows the General formula to expand the algebric equations by using Binomial Theorem,

According to theorem, expansion goes as following for any of the algebric equation containing any positve power,

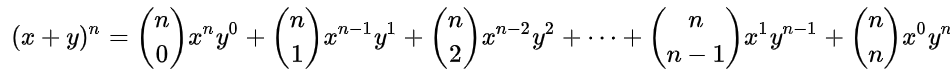
As after getting done by expansion one task remains pending that is to calculate the Binomial Coefficients (ⁿC_k)

Binomial Coefficients gives (ⁿC_k) combinations to choose k elements from n-element set.

How to calculate Binomial Coefficient ?

Binomial coefficient (ⁿC_k) is calculate by computing according to following expansion,

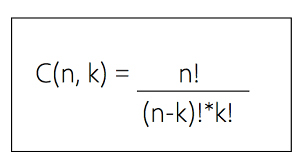
As per the above expansion, Binomial Coefficients (ⁿC₀, ⁿC₁, ⁿC₂...ⁿC_n) of Binomial Theorem are computed.

Example :
³C₂ :
= 3! / ((3 - 2)! * 2!)
= 3! / (1! * 2!)
= 3! / (1 * 2)
= 3! / 2
= 6 / 2

The number of permutation on a set of n elements is given by n!
Note :

• 0! = 1
• 1! = 1

Naive Approach

The value of C(n,k) can be recursively calculated because of the only identity mentioned below :

C(n, k) = C(n-1, k-1) + C(n-1, k) 

This hold true because:

C(n, k) = n! / (k! * (n-k)!)
        = (n-1)! * n / (k! * (n-k)!)
        = (n-1)! * n / ((k-1)! * k * (n-k-2)! * (n-k-1) * (n-k))
        = (n-1)! / ((k-1)! * (n-k-1)!) * (n / k * (n-k))
        = [(n-1)! / ((k-1)! * (n-k-1)!)] * (1/(n-k) + 1/k)
        = (n-1)! / ((k-1)! * (n-k)!) + (n-1)! / (k! * (n-k-1)!)
        = C(n-1, k-1) + C(n-1, k) 

This has made the idea clear.

Note :
C(n, 0) = 1
C(n, n) = 1

The idea to implement the above recursive relation using a recursion function with base conditions. Following is the pseudocode:

int recursiveBinomialCoefficientMethod(int n,int k)
{
    if(k == n or k == 0)
        return 1;
    return (recursiveBinomialCoefficientMethod(n-1,k-1)+recursiveBinomialCoefficientMethod(n-1,k));
}

Implementation of Naive approach:

#include <iostream>
class BinomialCoefficient
{
public:
    BinomialCoefficient(unsigned int n, unsigned int k) : n(n), k(k) { }
    unsigned int recursiveBinomialCoefficientMethod(int n, int k);
private:
    unsigned int n, k;
};
unsigned int BinomialCoefficient :: recursiveBinomialCoefficientMethod(int n, int k)
{
    if(k == n or k == 0)
        return 1;
    return (recursiveBinomialCoefficientMethod(n - 1, k - 1) + recursiveBinomialCoefficientMethod(n - 1, k));
}
int main()
{
    unsigned int valueOfN, valueOfK;
    std::cout << "\nEnter the value of n : ";
    std::cin >> valueOfN;
    std::cout << "\nEnter the value of k : ";
    std::cin >> valueOfK;
    BinomialCoefficient aBinoCoeff(valueOfN, valueOfK);
    std::cout << "Value of C(" << valueOfN << ", " << valueOfK << ") : " << aBinoCoeff.recursiveBinomialCoefficientMethod(valueOfN, valueOfK);
}

Input

Enter the value of n : 4
Enter the value of k : 2

Output

Value of C(4, 2) : 6

Complexity

The Time and Space Complexities of code by using Naive Approach are :

• Time complexity: O(2n)
• Space complexity: k

In space complexity, k means, k frames will loaded in RAM containing the local varialbles declared in function with respective data-type which will depend directly on architecture of Operating System of Local Host Machine*

Approach Using Dynamic Programming

Basic Idea in using Dynamic Programming is implementing Pascal's Triangle.
Pascal's Triangle is the triangular arrangement of the binomial coefficients.

Algorithm

• Step 1 : Get the two inputs, the positive value of n and the non-positive value of k which denotes the k-th binomial coefficient in the Binomial Expansion.
• Step 2 : Allocate the array of size k + 1 with the value of 1 at 0-th index and rest with value 0.
• Step 3 : Next, generating the sequence of pascal's triangle, with the first row containing single element valued 1 which was already created in step 2.
• Step 4 : Further next consecutive rows of pascal's triangle are computed from the previous row by adding the two consecutive elements, but step 4 is to be carried out upto k-times, for enclosing n-value times.
• Step 5 : Stop.

Implementation

#include <iostream>
class BinomialCoefficient
{
public:
    BinomialCoefficient(unsigned int n, unsigned int k) : n(n), k(k) { }
    unsigned int DPBinomialCoefficientMethod(int n, int k);
private:
    unsigned int n, k;
};
unsigned int BinomialCoefficient :: DPBinomialCoefficientMethod(int n, int k)
{
    unsigned int nCr[k + 1];
    for (int l = 0; l < k + 1; ++l)
        nCr[l] = 0;
    nCr[0] = 1;
    for (int p = 1; p <= n; p++)
    {
        for (int q = std::min(p, k); q > 0; q--)
            nCr[q] = nCr[q] + nCr[q - 1];
    }
    return nCr[k];
}
int main()
{
    unsigned int valueOfN, valueOfK;
    std::cout << "\nEnter the value of n : ";
    std::cin >> valueOfN;
    std::cout << "\nEnter the value of k : ";
    std::cin >> valueOfK;
    BinomialCoefficient aBinoCoeff(valueOfN, valueOfK);
    std::cout << "Value of C(" << valueOfN << ", " << valueOfK << ") : " << aBinoCoeff.DPBinomialCoefficientMethod(valueOfN, valueOfK);
}

Input

Enter the value of n : 3
Enter the value of k : 2

Output

Value of C(4, 2) : 3

Complexity

The Time and Space Complexities of code by using Dynamic Programming Approach are :

• Time complexity: O(n*k)
• Space complexity: k