Control flow in Intermediate Code Generation

During the construction of the front end of a compiler, we implement statements using control flow. We translate the statements by inheriting a label next that marks the first instruction after the code for this statement.

In this article, we learn about control flow during the intermediate code generation phase of the compiler.

Table of contents.

1. Introduction.
2. Boolean expressions.
3. Short-circuit code.
4. Flow control statements.
5. Translating boolean expressions.
6. How to avoid redundant gotos.
7. Jumping code.
8. Summary.
9. References.

Introduction.

Translating if-else and while statements involves translating boolean expressions.While programming, we use boolean expressions to compute logical values and alter the flow of control.

The use of boolean expressions is determined by the syntactic context, e.g, an expression that follows the keyword if alters the flow of control, while an expression on the right side is used to denote a logical value.

Such syntactic contexts are specified in several ways, we can use two different non-terminals, use inherited attributes, or set a flag during parsing.
We can also build a syntax tree then invoke different procedures for the two different uses of boolean expressions.

Boolean expressions

Boolean expressions comprise of boolean operators denoted by && - (AND), || - (OR), ! - (NOT).
Relational expressions are in the form of ${\mathrm{E}}_1$ rel ${\mathrm{E}}_2$ where ${\mathrm{E}}_1$ and ${\mathrm{E}}_1$ are arithmetic expressions.
We will consider boolean expressions generated using the following grammar.
B $\to$ B || B | B && B | !B | (B) | E rel E | true | false

The attribute rel.op is used to indicate the operator represented by rel among the 6 comparison operators <, <=, =, !=, > or >=.
It is conventional to assume that || and && are left-associative and || has the lowest precedence, then && and finally !.

Given an expression ${\mathrm{B}}_1$ || ${\mathrm{B}}_2$, if we determine that ${\mathrm{B}}_1$ is true then we can conclude the entire expression if true without evaluating ${\mathrm{B}}_2$. Similarly, given ${\mathrm{B}}_1$ && ${\mathrm{B}}_{\mathrm{s}}$, if ${\mathrm{B}}_1$ is false, the entire expression is false.

Short-circuit code

In a short-circuit code, boolean operators such as &&, ||, and ! translate into jumps. Instead, if the operators themselves appear in the code, the value of the boolean expression is represented by a position in the code sequence. An example is shown below;

We have the statement:
if(x < 100 || x > 200 && x != y) x = 0;

The statement is translated into the following code segment;

    if x < 100 goto L2
    ifFalse x > 200 goto L1
    ifFalse x != y goto L1
L2: x = 0
L1:

In the above translation, the boolean expression is true if the control reaches label 2. If the expression is false, control goes to L1 skipping L2 and the assignment x = 0.

Flow-of-control statements

In this section, we consider the translation of boolean expressions into three-address code in the context of statements generated by the following grammar;

S → if(B) ${\mathrm{S}}_1$
S → if(B) ${\mathrm{S}}_1$ else ${\mathrm{S}}_2$
S → while(B) ${\mathrm{S}}_1$

In the productions, non-terminal B represents a boolean expression while non-terminal S represents a statement.

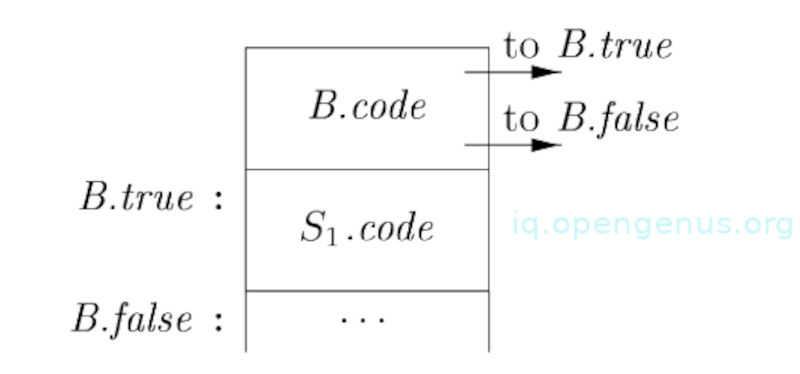
The translation of if(B) ${\mathrm{S}}_1$ consists of B.code followed by ${\mathrm{S}}_1$.code as can be seen in the image below;
(1).

(2).
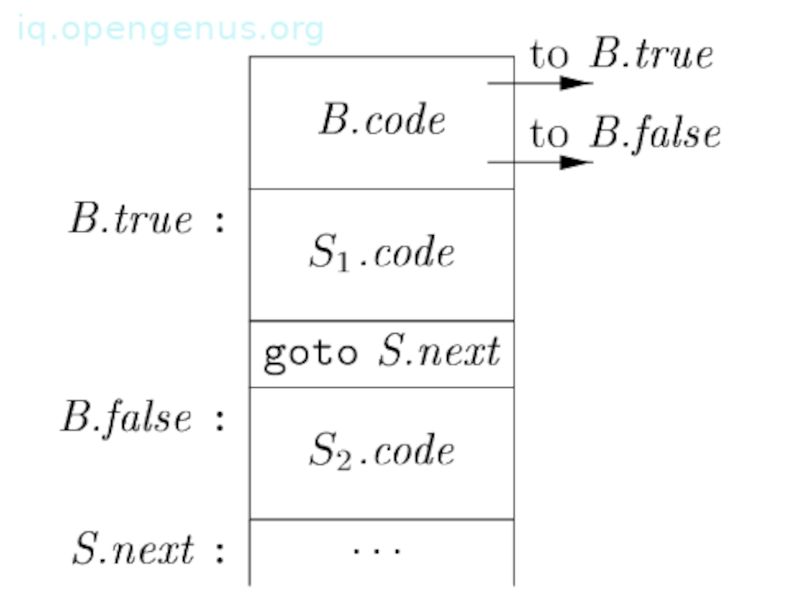
The if-else translation

(3).
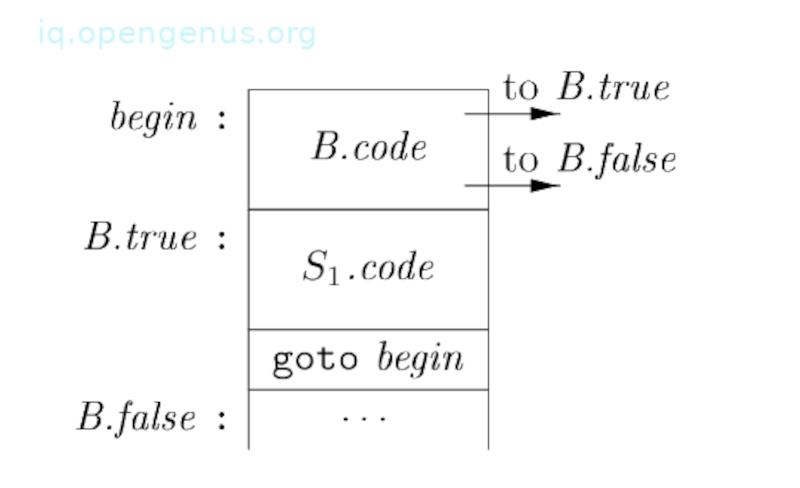
The while translation

Inside B.code we have jumps based on the value of B. If the value is true, control flows to the first instruction of ${\mathrm{S}}_1$.code otherwise B is false, therefore control flows to the instruction that follows ${\mathrm{S}}_1$.code.

Inherited attributes are used to manage labels for B.code and S.code. With a boolean expression B, two labels B.true and B.false are associated with each other if B is false.
We use statement S to associate the inherited attribute S.next that denotes a label for the instruction immediately following the code for S.
In other cases, the instruction that follows S.code is a jump to another label L.
A jump to L from S.code is avoided using S.next.

We have the following Syntax-directed definition that produces a three-address code for boolean expressions in the context of if, if-else and while statements.
(4).

Generating three-address code for booleans;
(5).

We have a program that consists of a statement that is generated by P → S. Semantic rules associated with this production initialize S.next to a new label.
P.code will consist of S.code which is followed by a new label S.next. assign in the production S → assign. This acts as a placeholder for the assignment statement.

In translating S → if(B) ${\mathrm{S}}_1$, semantic rules as shown in image (4) create a new label B.true then attach it to the first three-address instruction that is generated for ${\mathrm{S}}_1$.

By setting B.false to S.next, we make sure that control skips code for ${\mathrm{S}}_1$ if B results in a false.

Translating if-else statement that is S → if(B) ${\mathrm{S}}_1$ else ${\mathrm{S}}_2$, the code for the boolean expression B has jumps out of it to the first instruction of the code for ${\mathrm{S}}_1$ if B is true and to the first instruction of the code for ${\mathrm{S}}_2$, if B is false as can be seen from image (2).
Furthermore, control flows from ${\mathrm{S}}_1$ and ${\mathrm{S}}_2$ to the three-address instruction that immediately follows code for S. S.next is its label which is also an inherited attribute.
S.next is an explicit goto that appears after code for ${\mathrm{S}}_1$ to skip code for ${\mathrm{S}}_2$
After ${\mathrm{S}}_2$, we don't need any goto since ${\mathrm{S}}_2$.next will be similar to S.next.

For translating S → while(B) ${\mathrm{S}}_1$, we form its code from B.code and ${\mathrm{S}}_1$.code. This is seen from image (3).
The local variable begin holds a new label that is attached to the first instruction for this while statement, which is also the first instruction for B.
A variable is preferred to an attribute since begin is local to the semantic rules for this production.
Inherited label S.next marks the instruction where control must flow to, that is, when B is false, therefore, B.false is set to S.next. B.true which is a new label is attached to the first instruction for ${\mathrm{S}}_1$. Code for B generates a jump to this label, that is, if B is true.
Following the code for ${\mathrm{S}}_1$, we place the instruction goto begin. This causes a jump back to the start of the code for boolean expressions. Keep in mind that ${\mathrm{S}}_1$.next is currently set to the label begin, therefore, jumps within ${\mathrm{S}}_1$.code can go directly to begin.

Code for S → ${\mathrm{S}}_1$ ${\mathrm{S}}_2$ consists of code for ${\mathrm{S}}_1$ that is followed by code for ${\mathrm{S}}_2$. Semantic rules manage labels, the first instruction after ${\mathrm{S}}_1$ is the beginning of the code for ${\mathrm{S}}_2$, and the instruction after code ${\mathrm{S}}_2$ code, is the instruction after code for S.

Control-flow translation of boolean expressions.

Semantic rules for boolean expressions in image (5) complement semantic rules for image (4). As we can see from the code layout in images (1-3), a boolean B is translated into three-address instructions that evaluate B using conditional and unconditional jumps to one of two labels, these are B.true and B.false, the former is B is true and the latter otherwise.

Now, we have the following 4th production for B → ${\mathrm{E}}_1$ rel ${\mathrm{E}}_2$, is translated into a comparison three-address instruction with jumps to appropriate locations.
For example, if we have B with the form of a < b. It translates to;

if a < b goto B.true
goto B.false

For the other productions, we translate them as follows;

1. If B is in the form of ${\mathrm{B}}_1$ || ${\mathrm{B}}_2$, if B is true, we know that B is true, therefore ${\mathrm{B}}_1$.true is similar to B.true. If ${\mathrm{B}}_1$ is false, B2 must be evaluated. Therefore we make, ${\mathrm{B}}_1$.false the label of the first instruction in the code for ${\mathrm{B}}_2$. True and false exits for ${\mathrm{B}}_2$ are similar to true and false exits of B.
2. Translations of ${\mathrm{B}}_1$ && ${\mathrm{B}}_2$ are similar.
3. No code is needed for expression B in the form of !${\mathrm{B}}_1$. Here we just interchange true and false exits of B to get those for ${\mathrm{B}}_1$.
4. The constants true and false translate into jumps to B.true and B.false.

How to avoid redundant gotos.

From the if statement from section 3 (Short-Circuit code), the comparison x > 200 translates into the following;

    if x > 200 goto L4
    goto L1
L4: ...

Consider the following instruction;

    ifFalse x > 200 goto L1
L4: ...

The above ifFalse instruction takes advantage of the natural flow of instructions from one to the next in sequence and therefore control simply falls through to L4 if x > 200 and thus a jump is avoided.

From the code layouts from images 1, 2 and 3, the statement ${\mathrm{S}}_1$ follows code for the boolean expression B. Using a special label fall which states, 'don't generate any jump', we adapt semantic rules from images 4 and 5 so as to allow control to fall through from the code for B to the code for ${\mathrm{S}}_1$.
The new rules for S → if(B) ${\mathrm{S}}_1$ from image 4 set B.true to the label fall;

B.true = fall
B.false = ${\mathrm{S}}_1$.next = S.next
S.code = B.code || ${\mathrm{S}}_1$.code

In a similar way, rules for if-else and while statements set B.true to fall.

Now, we adapt semantic rules for boolean expressions which allows control to fall through when possible. Given the following rules for B → ${\mathrm{E}}_1$ rel ${\mathrm{E}}_2$;
(6).

We generate two instructions as shown in image 5, if both B.true and B.false are explicit labels, meaning neither equals fall., Otherwise, if B.true is explicit then B.false must be fall and thus they generate an if instruction that lets control fall through if the condition is false.
Conversely, if B.false is explicit, then they generate an ifFalse instruction. In the last case, both B.true and B.false are fall, here no jump is generated.

We have the following semantic rules for B → B1 || B2;
(7).

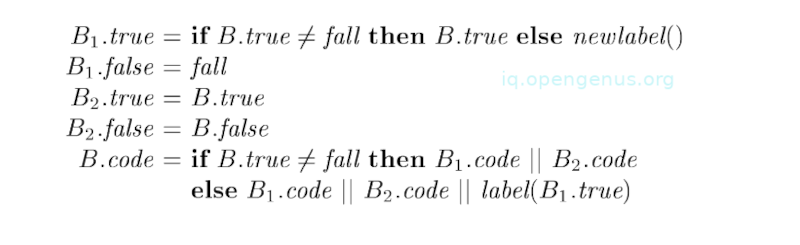
Here the meaning of the label fall for B is different from the meaning for ${\mathrm{B}}_1$. If B.true is fall, that is, control falls through B, if B evaluates to true. Although B evaluates to true if ${\mathrm{B}}_1$ also evaluates to true, ${\mathrm{B}}_1$.true must make sure that control jumps over the code for ${\mathrm{B}}_2$ to get to the next instruction after B.

Also, if ${\mathrm{B}}_1$ evaluates to false, B's truth-value is determined by the value of ${\mathrm{B}}_2$ and therefore rules from image 7 make sure that ${\mathrm{B}}_1$.false corresponds to control falling through from ${\mathrm{B}}_1$ to the code for ${\mathrm{B}}_2$.

Also note that the semantic rules for B → ${\mathrm{B}}_1$ && ${\mathrm{B}}_2$ will be similar to those of image 7.

Boolean values and jumping code.

Apart from using boolean expressions to change the flow of control in statements, boolean expressions can also be evaluated for their values.

For example, x = true or x = a > b.

An effective way of handling both these roles of boolean expressions is to construct a syntax tree for expressions using one of the following approaches.

1. Use two passes. Here we build a complete syntax tree for the input the traverse the tree using depth-first, computing translations specified by semantic rules.
2. Use a single pass for statements and two passes for expressions. Here we translate E in while (E) ${\mathrm{S}}_1$ before ${\mathrm{S}}_1$ is examined. The translation of ${\mathrm{S}}_1$ would then be done by constructing the tree and traversing it.

We have the following grammar that has a single nonterminal E for expressions;

S → id = E; | if(E) S | while(E)S | S S
E → E || E | E && E | E rel E | E + E | (E) | id | true | false

The non-terminal E governs the flow of control in S → while(E) ${\mathrm{S}}_1$, it also denotes a value S → id = E; and E → E + E.

We handle the two roles of expressions by using separate code generation functions. We assume that an attribute E.n denotes the syntax tree node for an expression E and that nodes are objects.
We have the method jump that generates the jumping code at an expression node and the method rvalue that generates code for computing the value of the node into a temporary.

When E appears in S → while(E) ${\mathrm{S}}_1$, the method jump is called at the node E.n. jump is implemented based on the rules for boolean expressions as can be seen from image 5.
By calling E.n.jump(t, f), jumping code is generated, here t represents a label for for the first instruction of ${\mathrm{S}}_1$.code and f represents the label for S.next.

When E appears in S → id = E;, the method rvalue is called at E.n node. If E is of the form ${\mathrm{E}}_1$ + ${\mathrm{E}}_2$, E.n.rvalue generates code. If E is of the form ${\mathrm{E}}_1$ && ${\mathrm{E}}_2$, we will first generate the jumping code for E then assign true or false to a new temporary t at the true and false exits from the jumping code.

Summary.

While programming, we use boolean expressions for two reasons, to alter the flow of control or to compute logical values. The use of boolean expressions is determined by the syntactic context used.

In short-circuit code, boolean operators such as &&, ||, and ! are translated into jumps.

References.

Compilers Principles, Techniques, & Tools - Alfred V. Aho Monica S. Lam