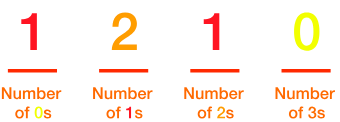Autobiographical Numbers

In this article, we have explored the idea of Autobiographical Numbers along with the algorithm to find Autobiographical Numbers, implementation and Time Complexity analysis.

Introduction

In this article, we will learn about Autobiographical Numbers.

• As we all know that an Autobiography means a self written biography, hence Autobiographical Numbers are those numbers who tell everything about themselves.

• An Autobiographical Number is a number N such that the first digit counts how many zeroes are there in N, the second digit counts how many ones are there in N, the third digit counts how many twos are there in N so on.

• Lets understand it with the help of this example.
  
  
  

• Explanation: In the above example, In the number integer 0 has occured one time, integer 1 has occured two times, integer 2 has occured one times and finally integer 3 has occured zero times. Hence 1210 clearly tells everything about its structure hence, it is an Autobiographical Number.

Some Interesting Facts

We all have known the definition of Autobiographical Numbers. Now let us learn some of the interesting facts and properties of all such numbers.

• The First Autobiographical number 1210.

• The total number of digits in the number and the sum of the digits in the number are equal.

• Let us find all autobiographical numbers using the “zoom-in” method.

  1. By definition, the autobiographical numbers can’t have more than 10 digits ie. they can't be too huge.
  2. The number of zeroes is not a zero since The first digit is the number of zeroes in the number itself and self-respecting integers do not start with a zero.
  3. The sum of the digits will not be more than 10 since the sum of the digits in an autobiographical number equals the number of the digits.
  4. Hence we get a resulting statement that the sum of all the digits, except for the first one, is equal to the number of non-zero digits plus 1.
  5. Simply, other than the first digit, the set of all other non-zero digits consists of several ones and 1 two.
  6. Here is the full set of autobiographical numbers: 1210, 2020, 21200, 3211000, 42101000, 521001000, 6210001000.

Program to find all Autobiographical Numbers of a given length

• The problem is simple you just need to find all the Autobiographical Numbers whose length is equal to N where N is total number of digits in the number.
• Naive Approach :
  1. The approach implemented below is quiet easy. We just traverse through all numbers in given range
  2. For every number, we count the total number of occurances of the index values as per the definition of Autobiographical Numbers.
• Example
  1. If the index is 0 then count the total occurances of 0 in the number.
  2. If the count is equal to the index then we proceed for the next index and so on.
  3. If count is not equal to the index then we stop iterating for that number and proceed to check next number.

bool isAutoBiographyNum(int number)
{
    Checks whether number is Autobiographical or not by two nested loops.
    First loop takes the index and second loop tracks the count for every value equal to index.
}
void check(int n)
{
    Provides every number within the range formed by n digits
}

Implementation

• This program finds all Autobiographical Numbers of a given length :

#include <bits/stdc++.h>
using namespace std;

bool isAutoBiographyNum(int number)
{
     int count, position ,size, digit;
     count=0;
     string NUM;

     //convert to string to check every integer for index and value easily 
     NUM = to_string(number);
     size=NUM.length();

     //iterate for every digit to check for their total count
     for (int i = 0;i < size;i++)
     {
         //convert digit in character format to integer format since we can 
         //only check equality for same data type.
         position = NUM[i]- '0';

         count = 0;
         //check occurance of every number and count them
         for (int j = 0; j < size; j++)
          {
             digit = NUM[j] - '0';
             if (digit == i)
               count++;
         }
         //if any position mismatches with total count then return with false
         //else continue with loop and check for next position
         if (position != count)
             return false;
     }
     return true;
}
//function to iterate in range to find numbers
void check(int n)
{
      int left, right, found = 0;

      cout<<"For N = "<<n<<" :\n";
      left = pow(10, n - 1);

      // Right boundary of interval
      right = pow(10, n) - 1;

      //iterate from left boundary to right boundary and check for all
      //the numbers in the range
      while(left<=right)
      {
         if (isAutoBiographyNum(left)!=0) {
             found = 1;
             cout << left << "  ";
         }
       left++;
      }
      if (found==0)
         cout << "There is no number for N="<<n;
      cout<<"\n";
}

int main()
{
      int n;
      n=3;
      check(n);
      n=4;
      check(n);
      n=5;
      check(n);
return 0;
}

OUTPUT :

For N = 3 :
There is no number for N=3
For N = 4 :
1210  2020  
For N = 5 :
21200

Time Complexity

• Time complexity of isAutoBiographyNum function : Θ(n^2)
• Time complexity of check function : Θ(10^n)
• Time complexity of complete program : Θ(n^2.10^n)

With this article at OpenGenus IQ, you must have got a complete idea about interesting Autobiography Numbers. Enjoy.