Euclidean vs Manhattan vs Chebyshev Distance

Euclidean distance, Manhattan distance and Chebyshev distance are all distance metrics which compute a number based on two data points. All the three metrics are useful in various use cases and differ in some important aspects which we bring out in this article.

Visual difference

This image summarizes the difference in the three distance metrics:

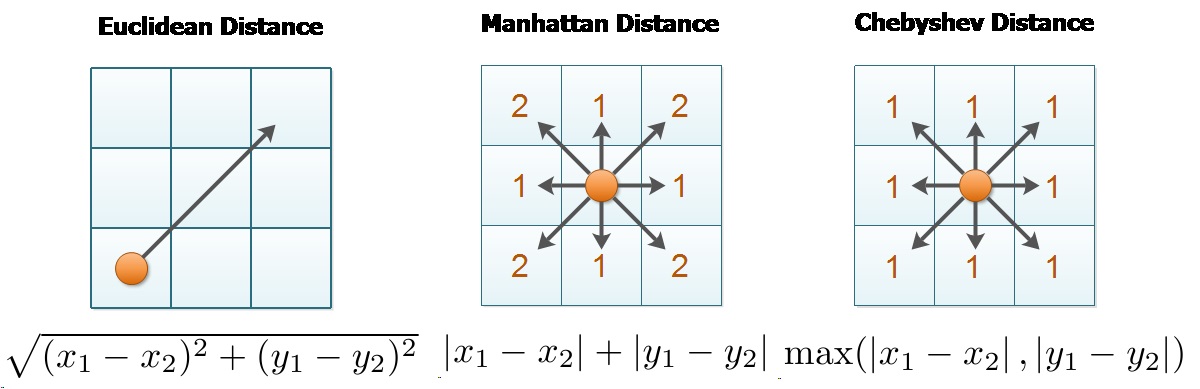
Computation

In a N dimensional space, a point is represented as (x1, x2, ..., xN).

Consider two points P1 and P2:

P1: (X1, X2, ..., XN)
P2: (Y1, Y2, ..., YN)

Then, the euclidean distance between P1 and P2 is given as:

$$ \sqrt{{(x1-y1)}^2\ +\ {(x2-y2)}^2\ +\ ...\ +\ {(xN-yN)}^2}
$$

The manhattan distance between P1 and P2 is given as:

$$ |x1-y1|\ +\ |x2-y2|\ +\ ...\ +\ |xN-yN|}
$$

The chebyshev distance between the two points P1 and P2 is:

Chebyshev distance = MAXIMUM (|xi - yi|) where i is 1 to N

Usage in Chess

In chess, all the three distances are used as follows:

• the distance between squares on the chessboard for rooks is measured in Manhattan distance
• kings and queens use Chebyshev distance
• bishops use the Manhattan distance (between squares of the same color) on the chessboard rotated 45 degrees, i.e., with its diagonals as coordinate axes.
• To reach from one square to another, only kings require the number of moves equal to the distance (euclidean distance) rooks, queens and bishops require one or two moves