Reading time: 15 minutes

Manhattan distance is a distance metric between two points in a N dimensional vector space. It is the sum of the lengths of the projections of the line segment between the points onto the coordinate axes. In simple terms, it is the sum of absolute difference between the measures in all dimensions of two points.

Table of contents:

1. Basics of Manhattan distance
2. Properties of Manhattan distance
3. Manhattan distance in 2D space
4. Manhattan distance in N-D space
5. Manhattan distance & Minkowski distance
6. Applications of Manhattan distance

Basics of Manhattan distance

It is, also, known as L1 norm and L1 metric.

It is used extensively in a vast area of field from regression analysis to frquency distribution. It was introduced by Hermann Minkowski.

The concept of Manhattan distance is captured by this image:

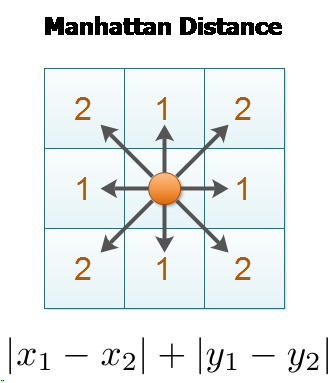
Properties of Manhattan distance

Properties of Manhattan distance are:

• There are several paths (finite) between two points whose length is equal to Manhattan distance

• A straight path with length equal to Manhattan distance has two permitted moves:

  • Vertical (one direction)
  • Horizontal (one direction)

• For a given point, the other point at a given Manhattan distance lies in a square:

Manhattan distance in 2D space

In a 2 dimensional space, a point is represented as (x, y).

Consider two points P1 and P2:

P1: (X1, Y1)
P2: (X2, Y2)

Then, the manhattan distance between P1 and P2 is given as:

$$ {{|x1-x2|\ +\ |y1-y2|}$$

Manhattan distance in N-D space

In a N dimensional space, a point is represented as (x1, x2, ..., xN).

Consider two points P1 and P2:

P1: (X1, X2, ..., XN)
P2: (Y1, Y2, ..., YN)

Then, the manhattan distance between P1 and P2 is given as:

$$ |x1-y1|\ +\ |x2-y2|\ +\ ...\ +\ |xN-yN|}
$$

Manhattan distance & Minkowski distance

Manhattan distance is a special case of Minkowski distance.

When P=1 for Minkowski distance, we get Manhattan distance.

Applications of Manhattan distance

Manhattan distance is frequently used in:

1. Regression analysis: It is used in linear regression to find a straight line that fits a given set of points

2. Compressed sensing: In solving an underdetermined system of linear equations, the regularisation term for the parameter vector is expressed in terms of Manhattan distance. This approach appears in the signal recovery framework called compressed sensing

3. Frequency distribution: It is used to assess the differences in discrete frequency distributions