
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes
Chebyshev distance is a distance metric which is the maximum absolute distance in one dimension of two N dimensional points. It has real world applications in Chess, Warehouse logistics and many other fields.
It is, also, known as Tchebychev distance, maximum metric, chessboard distance and L∞ metric.
It is named after Pafnuty Chebyshev, a Russian mathematician who is the recipient of the Demidov Prize and is known for his work on probability, statistics, mechanics, analytical geometry and number theory.
The concept of Chebyshev distance is captured by this image:
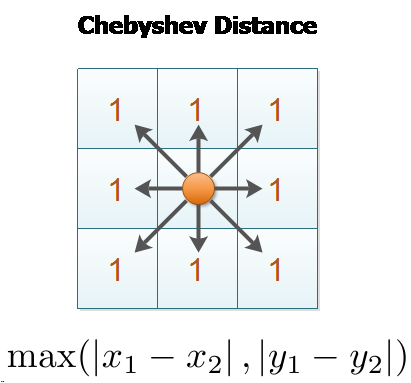
Properties
Properties of Chebyshev distance are:
-
The two dimensional Manhattan distance also has circles in the form of squares, with sides of length √2r, oriented at an angle of π/4 (45°) to the coordinate axes, so the planar Chebyshev distance can be viewed as equivalent by rotation and scaling to the planar Manhattan distance
-
A sphere formed using the Chebyshev distance as a metric is a cube with each face perpendicular to one of the coordinate axes, but a sphere formed using Manhattan distance is an octahedron: these are dual polyhedra, but among cubes, only the square (and 1-dimensional line segment) are self-dual polytopes
Example
Consider two points P1 and P2 with co-ordinates as follows:
P1 = (p1, p2, ..., pN)
P2 = (q1, q2, ..., qN)
The chebyshev distance between the two points P1 and P2 is:
Chebyshev distance = MAXIMUM (|pi - qi|) where i is 1 to N
Applications
Applications of Chebyshev distance are:
-
Chess: The minimum number of moves needed by a king to go from one square on a chessboard to another equals the Chebyshev distance between the centers of the squares
-
Warehouse logistics: The Chebyshev distance is sometimes used in warehouse logistics as it effectively measures the time an overhead crane takes to move an object
