
Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
Reading time: 15 minutes
Euclidean distance is the shortest distance between two points in an N dimensional space also known as Euclidean space. It is used as a common metric to measure the similarity between two data points and used in various fields such as geometry, data mining, deep learning and others.
It is, also, known as Euclidean norm, Euclidean metric, L2 norm, L2 metric and Pythagorean metric.
The concept of Euclidean distance is captured by this image:
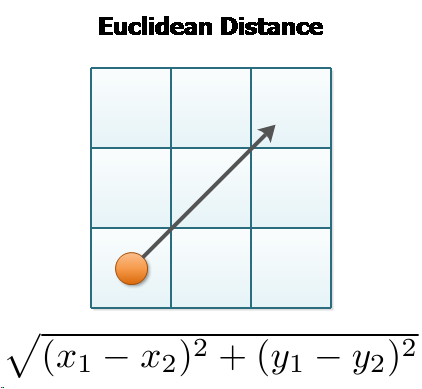
Properties
Properties of Euclidean distance are:
-
There is an unique path between two points whose length is equal to Euclidean distance
-
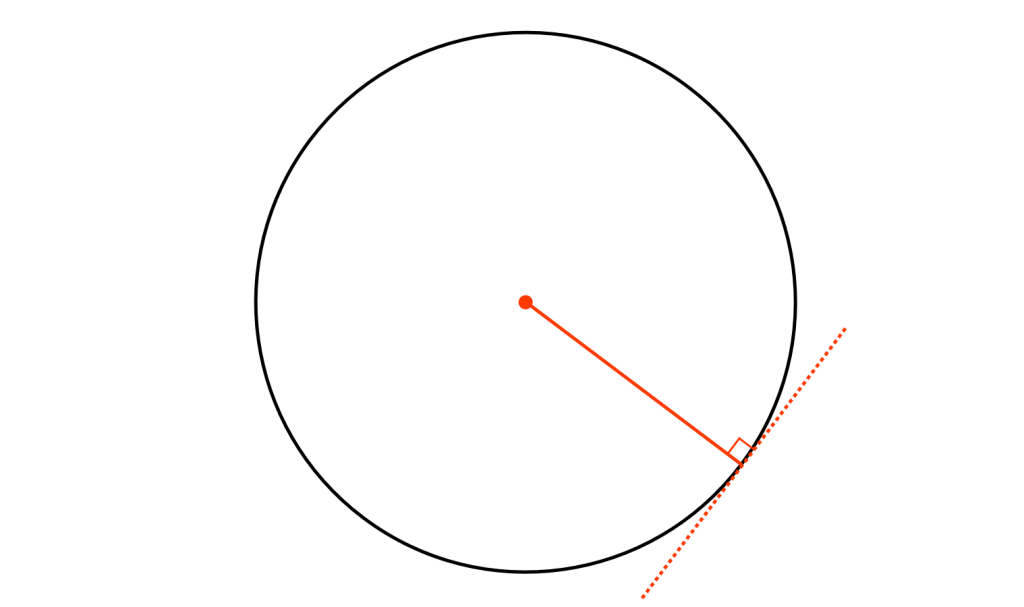
For a given point, the other point lies in a circle such that the euclidean distance is fixed. The radius of the circle is the fixed euclidean distance.
Euclidean distance in 2D space
In a 2 dimensional space, a point is represented as (x, y).
Consider two points P1 and P2:
P1: (X1, Y1)
P2: (X2, Y2)
Then, the euclidean distance between P1 and P2 is given as:
$$ \sqrt{{(x1-x2)}^2\ +\ {(y1-y2)}^2}
$$
Euclidean distance in N-D space
In a N dimensional space, a point is represented as (x1, x2, ..., xN).
Consider two points P1 and P2:
P1: (X1, X2, ..., XN)
P2: (Y1, Y2, ..., YN)
Then, the euclidean distance between P1 and P2 is given as:
$$ \sqrt{{(x1-y1)}^2\ +\ {(x2-y2)}^2\ +\ ...\ +\ {(xN-yN)}^2}
$$
Applications
Euclidean distance is frequently used in:
-
Euclidean Geometry: To find the shortest distance between two points in an Euclidean space and the ;ength of a straight line between two points
-
Cluster Analysis: This metric is commonly used in clustering algorithms such as K-means
-
Data Science: It is used as a simple metric to measure the similarity between two data points
