Fractional Cascading in Binary search

In this article, fractional cascading in binary search will be covered. We will go through the reason, implementation and time complexity of the binary cascade.

Fractional Cascading is an optimization over Binary Search to perform Binary Search on K sorted lists to improve the time complexity from O(K logN) to O(logN + K).

As we know that the binary search is the algorithm which is used to find the position or existance of the target value in a sorted array by repeatedly dividing the search interval in half. First, it starts by taking the whole array. If the target value is less than the middle element of the interval, consider the interval to the lower half (high key = middle-1), else consider the interval to the upper half (low key = middle+1). Its complexity will be O(log(n)).

It is also called as Logarithmic search or half-interval search. This algorithm could find the exact target value as well as just greater element than target value.

What if we want to search the target value or just smaller value than target value in given "k" sorted arrays each of size "n" ?

We could do it by iterative binary search approach, as Iterative binary search approach is just using k times binary search for finding target value/just smaller value than target value in k lists. So, as it does'nt uses any extra space, its space complexity is O(1),and the time complexity is O(k log(n)).

But, can we do it more better in time complexity? The answer is yes!
For the sake of better complexity, we can optimise this approach by also using extra space, and the method to do so is called as Unified Binary Search. In this method,
we may merge all the k lists into a single big list L, and associate with each item x of L a list of the results of searching for x in each of the smaller lists L[i].
We use preprocessing in which basically all the positions of elements in k arrays are precomputed and then in one go of a binary search, the target value/just greater element than target value in k arrays is found. However, this solution pays a high penalty in space complexity: it uses space O(kn) as each of the n items in L must store a list of k search results.

But, if we want it's more optimised solution with less or space complexity of O(n), that method is called as "FRACTIONAL CASCADING".

Fractional cascading:

Fractional cascading is just one smart method to do the same work of finding target in k sorted lists in perfect complexity to save compilation time a lot, as only one time binary search will work for it, which is absolutely better than above discribed methods. It allows this same searching problem to be solved with time and space bounds meeting the best of both worlds: query time O(log n + k), and space O(n).

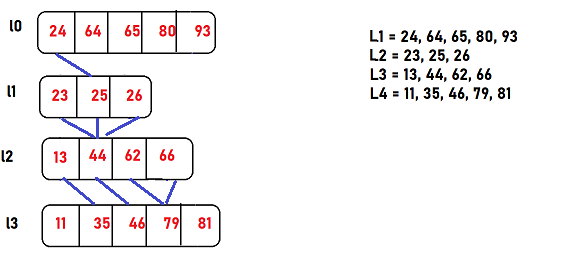
If we plan to make this method in such a way that, if once we apply the binary search, we could be able to find a range or exact item in i+1'th list, this is possible with the creation of connections/bridges between two continous lists.

Conecpt of making of connections:

So, the main point is making bridges/connections between the lists and the process of making connections between two consecutive lists may be imagined as following, for raw idea:

1. If we have k sorted lists, then we just have to connect each item of i'th list with the same item in i+1'th list, and this is only possible if same item exists in next list.
2. If same element doesnot exists in next element, just connect the current item of i'th list with the item in i+1'th list that will be just greater than the current item in upper list.
3. But, by chance if there's no just greater or the exact item in next list, continue with the same procedure for making connections of other items with every i'th list with items of i+1'th list, and condition will be i<k-1 , initialising from i=0.
4. These connections/bridges can be implemented using pointers, array indexes or graphs. This is also called as preprocessing.

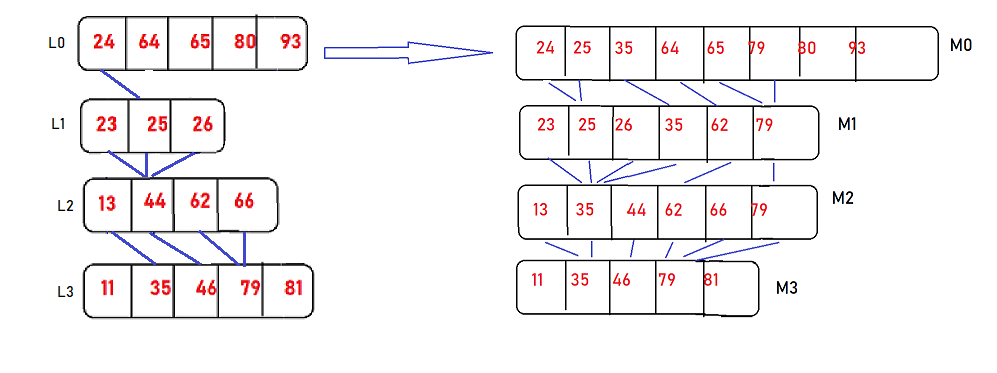
The fractional cascading solution is to store a new sequence of lists Mi. The final list in this sequence, Mk, is equal to Lk; each earlier list Mi is formed by merging Li with every second item from Mi+1. With each item x in this merged list, we store two numbers: the position resulting from searching for x in Li and the position resulting from searching for x in Mi+1. For the data above, this would give us the following lists:

Working of the Fractional Cascading :

Basically, what happens in this is, for any data structure of this type, we do a test case by applying binary search for target q in M1,and get from the resulting value the position of q in L1. Then , to find its position in Mi+1, we use the known position of q in Mi. The value associated with the position of q in Mi points to a position in Mi+1 that is either the correct result of the binary search for q in Mi+1 or is a single step away from that correct result, so stepping from i to i + 1 requires only a single comparison.

Lets consider the above case, and take the target value equal to 50. Remind that this time, we just need to consider the range of Mi by applying one time binary search, as after that the range in Mi will help finding the existance of target value in k sorted lists.
By applying binary search on M1, we got 64[1,5].The "1" in 64[1,5], tells us that the search for q in L1 should return L1[1] = 64. The "5" in 64[1,5] tells us that the approximate location of q in M2 is position 5.
More precisely, binary searching for q in M2 would return either the value 79[3,5] at position 5, or the value 62[3,3] one place earlier
By comparing q to 62, and observing that it is smaller, we determine that the correct search result in M2 is 62[3,3]. The first "3" in 62[3,3] tells us that the search for q in L2 should return L2[3], a flag value meaning that q is past the end of list L2.
The second "3" in 62[3,3] tells us that the approximate location of q in M3 is position 3. More precisely, binary searching for q in M3 would return either the value 62[2,3] at position 3, or the value 44[1,2] one place earlier.
A comparison of q with the smaller value 44 shows us that the correct search result in M3 is 62[2,3].
The "2" in 62[2,3] tells us that the search for q in L3 should return L3[2] = 62, and the "3" in 62[2,3] tells us that the result of searching for q in M4 is either M4[3] = 79[3,0] or M4[2] = 46[2,0]; comparing q with 46 shows that the correct result is 79[3,0] and that the result of searching for q in L4 is L4[3] = 79.
**Thus, we have found q in each of our four lists, by doing a binary search in the single list M1 followed by a single comparison in each of the successive lists.
**

import bisect
# This is the 2D array, having each list sorted
array_2d = [
    [24, 64, 65, 80, 93],
    [23, 25, 26],
    [13, 44, 62, 66],
    [11, 35, 46, 79, 81],
]
# this is the target to find in 2D array
X = 50


Min, Max = -1000000000, 1000000000
array_M1 = []
array_M1.insert(0, [x for x in array_2d[-1]])
for i in range(len(array_2d) - 2, -1, -1):
    array_M1.insert(0, sorted([x for k, x in enumerate(array_M1[0]) if k % 2] + array_2d[i]))

for l in array_M1:
    l.insert(0, Min)
    l.append(Max)

array_M1


# For each of the element in `array_2d` positions will hold
# the location where the element `array_2d[i][j]` will be inserted.
locations = []
for i in range(len(array_M1)):
    locations.append([])
    for j in range(len(array_M1[i])):
        locations[i].append([[]] * len(array_2d[i]))
        locations[i][j] = [-1] * 2


for i, l in enumerate(m_arr):
    for j, m in enumerate(m_arr[i]):
        locations[i][j] = [
            bisect.bisect_left(array_2d[i], array_M1[i][j]),
            0 if i == len(array_M1) - 1 else bisect.bisect_left(array_M1[i+1], array_M1[i][j]),
        ]

locations[:3]

def fractional_cascading_start(x): 
    locations_2 = []
    pos, next_pos = locations[0][bisect.bisect_left(array_M1[0], x)]
    locations_2.append(pos)
    for i in range(1, len(array_M1)):
        if x <= array_M1[i][next_pos-1]:
            pos, next_pos = locations[i][next_pos-1]
        else:
            pos, next_pos = locations[i][next_pos]
        locations_2.append(pos)
    return locations_2


#calling of the main function
fractional_cascading_start(X)

Time Complexity: O(k + log(n)).

Space Complexity: O(n)

Application of Fractional Cascading in Binary search :

1. Typical applications of fractional cascading involve range search data structures in computational geometry.
2. Fractional cascading in geometric data structures concerns point location in a monotone subdivision, that is, a partition of the plane into polygons such that any vertical line intersects any polygon in at most two points.
3. In the design of data structures for fast packet filtering in internet routers
4. As a model for data distribution and retrieval in sensor networks.

**This article covered almost all points about the reason to use and implementation of fractional cascading. I hope you all liked this article, and if you want to have look into related articles, do have a look below. Happy coding, learn to Grow. **