Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
In this problem, we are given a binary tree and a key k. We need to find out all the ancestors of k.
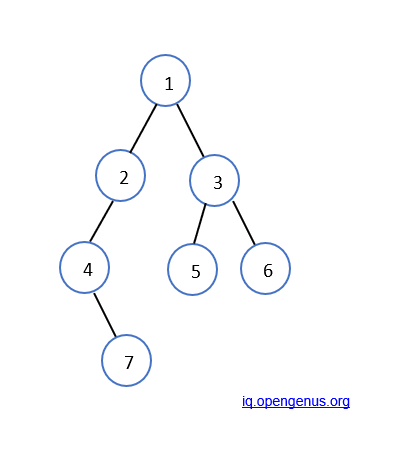
For example, if k = 7 and the given tree is -
Then, the ancestors of 7 will be 4,2 and 1.
You can simply solve this problem using standard traversal techniques like:
- Breadth First Search
- Depth First Search
- Level order traversal
The idea is to do that traversal recursively and return 1 when you reach the given node K and return 0 for all other cases. What this does is that: All nodes coming before the given node K get the return value of 1 and if we get 1, it means the current node is an ancestor.
This is a simple approach which you can take to use existing knowledge of BFS or DFS.
We will easily solve this problem using recusion:
- Let the recursive function be printAncestor(node, k), which will return a boolean (true/false).
- We will start from the root node with k=7. The function printAncestor(root, k) will be executed and it will recursively call its left and right nodes until k i.e 7 is found in that node, or till node = NULL.
- We will return true if k will be found in the node.
- We will print a node whenever true is returned from its left or right nodes. (That means the current node is the key's ancestor).
Code -
The following is the code to the above problem in C++
#include<bits/stdc++.h>
using namespace std;
/* A binary tree node having data,
pointer to left child and
a pointer to right child */
class node
{
public:
int data;
node* left;
node* right;
/* Constructor that allocates a new node with the
given data and NULL left and right pointers. */
node(int data)
{
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
/* If target is present in any node, print its ancestor and return true. Else, return false*/
bool printAncestors(struct node *root, int target)
{
/* base cases */
if (root == NULL)
return false;
if (root->data == target)
return true;
/* If target is present in either left or right subtree of this node, then print this node */
if ( printAncestors(root->left, target) ||
printAncestors(root->right, target) )
{
cout << root->data << " ";
return true;
}
/* Else return false */
return false;
}
/* Driver code*/
int main()
{
/* Construct the following binary tree
1
/ \
2 3
/ / \
4 5 6
/
7
*/
node *root = new node(1);
root->left = new node(2);
root->right = new node(3);
root->left->left = new node(4);
root->right->left = new node(5);
root->right->right = new node(6);
root->left->left->left = new node(7);
printAncestors(root, 7);
return 0;
}
Workflow
Let us walkthrough the problem with our given example, where k = 7 and the following binary tree is given -
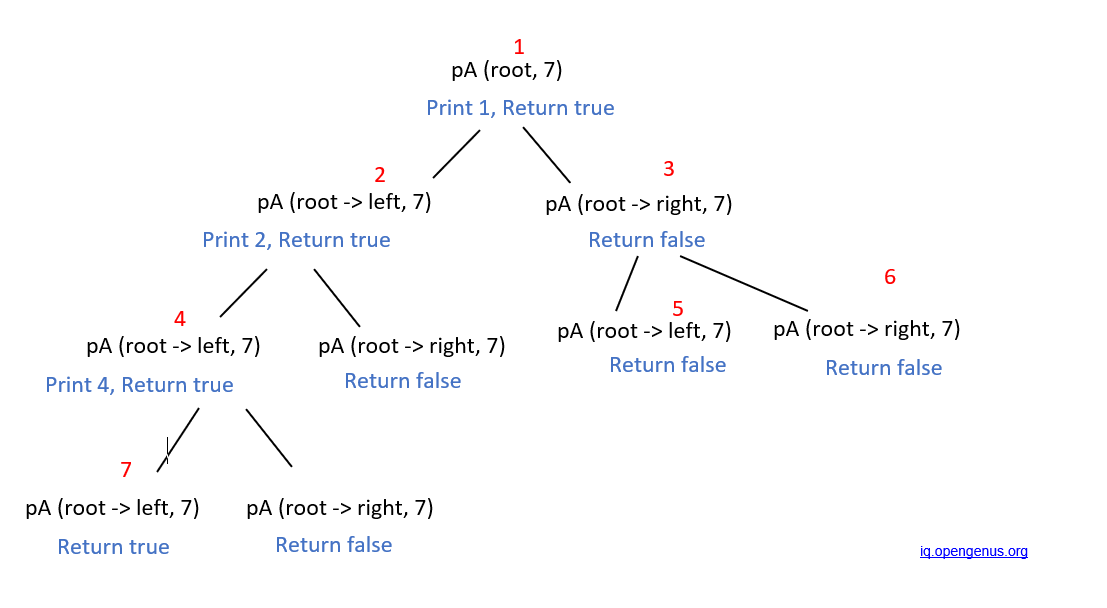
- The function printAncestor(root (1), 7) (the number in the bracket denotes the data stored at that particular node) will be called initially, which will recusrsively call its left and right subtrees until we get the function printAncestor(node (7), 7).
- printAncestor(node (7), 7) will return true in its parent node (4), hence the value 4 will be printed, and again we will return true.
- node (2) will receive true from its child, so it will print 2 and return true. This process is continued till the root node. Therefore, 4 2 1 is printed as the final answer.
The following graph depicts the recursion route for this problem -
Complexity
Time complexity: O(n)
Space complexity: O(n), where n is the number of nodes.
Hence, we have figured out how to find the ancestors of any given node.