Open-Source Internship opportunity by OpenGenus for programmers. Apply now.
We are given the root of a tree, and an integer k. We need to print all the nodes which are a distance k from the root.
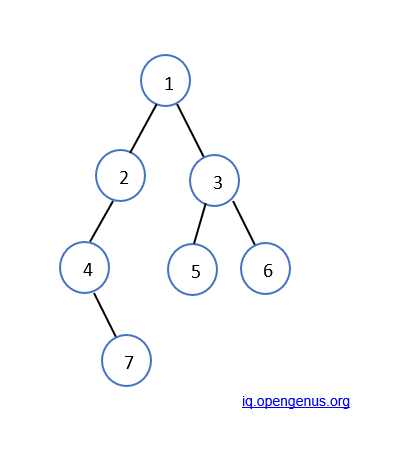
For example, if the given tree is:
Here, the root is 1. If k is 2, then the output should be 4, 5 and 6 as they are at a distance of 2 from the root.
This problem can be solved using a general traversal technique like:
- Breadth First Search
- Depth First Search
- Level Order Traversal
In Depth First Search (DFS) and Breadth First Search (BFS), we can keep track of the level of each node by adding 1 to each level of traversal. When the level is K, the current node is at a distance of K from the root node.
In Level Order traversal, we shall get all nodes at level K.
This problem can be easily solved using general recursion:
- We will make a recursion function, let's say printNodes(node * root, int k) .
- This function will recursively call itself in its left and right children, with a distance of k-1.
- Finally, when k=0 is encountered, we will print the value in the current node. This node will be at a distance of k from the root.
Walkthrough
Let us walk through the procedure with our given example.
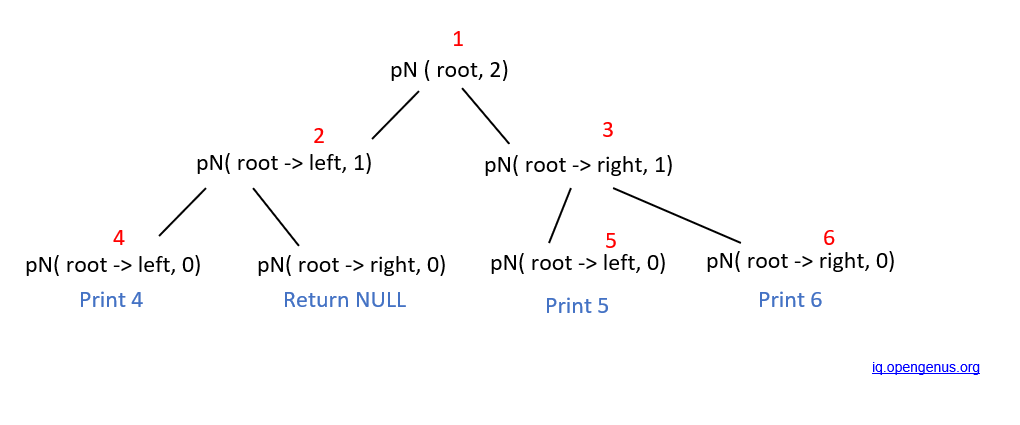
- Initially, the root of the tree is 1 and k = 2. Since k is not equal to 0, we will recursively call the tree with its left child as the root and k-1. Hence, the function printNodes( root->left, 1 ) will be called.
- Our new root will then be 2 and k =1. Again, k is not 0, hence we will call the function printNodes( root->left, 0 ).
- Now, our root is 4 and this time, k=0. So we will print the data in the given root, as this node will be at a distance of k=2 from the original root.
- Similarly, the recursive function will be called in the right subtrees until we get a NULL value, or until k=0.
The following graph depicts the recursion route. (The function name printNodes is abbreviated to pN)
Code
The following is the code to the above problem in C++
#include<bits/stdc++.h>
using namespace std;
/* A binary tree node has data,
pointer to left child and
a pointer to right child */
class node
{
public:
int data;
node* left;
node* right;
/* Constructor that allocates a new node with the
given data and NULL left and right pointers. */
node(int data)
{
this->data = data;
this->left = NULL;
this->right = NULL;
}
};
void printNodes(node *root , int k)
{
if(root == NULL)
return;
if( k == 0 )
{
cout << root->data << " ";
return ;
}
else
{
printNodes( root->left, k - 1 ) ;
printNodes( root->right, k - 1 ) ;
}
}
/* Driver code*/
int main()
{
/* Constructed binary tree is
1
/ \
2 3
/ / \
4 5 6
/
7
*/
node *root = new node(1);
root->left = new node(2);
root->right = new node(3);
root->left->left = new node(4);
root->right->left = new node(5);
root->right->right = new node(6);
root->left->left->left = new node(7);
printNodes(root, 2);
return 0;
}
Output -
4 5 6
Complexity -
Time complexity: O(n)
Space complexity: O(n) , where n is the no. of nodes.
Hence, we have found out how to find nodes at a distance of k from the root node, using recursion.