Find ancestors of a given node in a binary tree (Recursive + Iterative)

Given a binary tree, we are supposed to find the ancestors of a particular node. An ancestor is a node that is present in the upper layer of a given node. Since the problem revolves around binary trees, a particular node can have atmost 2 children so the ancestor of any given node will be its parent node and the ancestor of the parent node will be its parent node (grandparent node for the particular node in question). We will be printing the ancestors of a particular node until we reach the root of the binary tree.

Let us understand this using a figure.

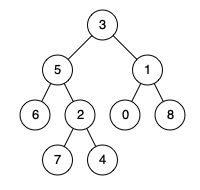
Ancestors of node 3: None (since the root node)
Ancestors of node 5: 3
Ancestors of node 1: 3
Ancestors of node 6: 5, 3
Ancestors of node 2: 5, 3
Ancestors of node 0: 1, 3
Ancestors of node 8: 1, 3
Ancestors of node 7: 2, 5, 3
Ancestors of node 4: 2, 5, 3

We will solve this using both:

• Recursive solution
• Iterative solution

Idea behind solving this problem

1. Recursive solution

To solve this problem using recursion, first traverse the binary tree in a postorder fashion. A postorder traversal is one where the left subtree is traversed first, followed by the right subtree and the root is traversed at the end. If the given node is found at either the left subtree of the right subtree for any node, the the current node in the traversal would be the ancestor of the node.

The algorithm for this approach is as follows:

1. Input the binary tree and the key_node whose ancestors are to be printed.
2. Traverse all the nodes of the tree and perform recursive post order traversal.
3. Until the key_node is found, traverse the left and right sub trees recursively.
4. Once the key_node is reached, return the data of the nodes in the path.

2. Iterative solution

To solve this problem using recursion, we need to store the parent node of all the nodes in the tree explicitly (using a map in C++ or a dictionary in Python). Then we would traverse the binary tree in an iterative preorder fashion. An iterative preorder traversal is similar to the regular preorder traversal: start at the root node and traverse the left subtree followed by traversing the right subtree. Set the parent pointer of each node and print the ancestors of the given node using the explicit map that is used to store all the nodes in the binary tree.

The algorithm for this approach is as follows:

1. Input the binary tree and the key_node whose ancestors are to be printed.
2. Traverse all the nodes of the tree and perform iterative post order traversal.
3. Stop the traversal when the desired key_node is reached.
4. Store the ancestors of the nodes while traversing in a stack.
5. Once we reach the key_node,print the stack.

Code implementation

Below is the code implementation of both the recursive as well as the iterative solution. The language of preference is C++. I have also created a Github repository that has the presented solution here as well as a solution in Python. You can visit this link if you wish to see the repository.

1. Recursive solution

#include <iostream>
using namespace std;
 
// Data structure to store a binary tree node
struct Node
{
    int data;
    Node *left, *right;
 
    Node(int data)
    {
        this->data = data;
        this->left = this->right = nullptr;
    }
};
 
// Recursive function to print all ancestors of a given node in a binary tree.
// The function returns true if the node is found in the subtree rooted at the
// given root node.
bool printAncestors(Node *root, int node)
{
    // if tree is empty
    if (root == nullptr) {
        return false;
    }
 
    // TRUE if given node found
    if (root->data == node) {
        return true;
    }
 
    // search node in left subtree
    bool left = printAncestors(root->left, node);
 
    // search node in right subtree
    bool right = false;
    if (!left) {
        right = printAncestors(root->right, node);
    }
 
    // if given node found in either left or right subtree,
    // then current node is ancestor of a given node
    if (left || right) {
        cout << root->data << " ";
    }
 
    // if a node is found, return TRUE
    return left || right;
}
 
int main()
{
    Node* root = nullptr;
 
    /* map of the binary tree in question
         3
       /   \
      /     \
     5       1
    / \     / \
   6   2   0   8
      / \
     7   4
    */
 
    root = new Node(3);
    root->left = new Node(5);
    root->right = new Node(1);
    root->left->left = new Node(6);
    root->left->right = new Node(2);
    root->right->left = new Node(0);
    root->right->right = new Node(8);
    root->left->right->left = new Node(7);
    root->left->right->right = new Node(4);
 
    int node = 8;
    printAncestors(root, node); // prints 1 3 as output
 
    return 0;
}

2. Iterative solution

#include <iostream>
#include <stack>
#include <unordered_map>
using namespace std;
 
// Data structure to store a binary tree node
struct Node
{
    int data;
    Node *left, *right;
 
    Node(int data)
    {
        this->data = data;
        this->left = this->right = nullptr;
    }
};
 
// Function to print root-to-leaf paths without using recursion
void rootToLeaf(unordered_map<int, int> parent, int key)
{
    while (key = parent[key]) {
        cout << key << " ";
    }
 
    cout << endl;
}
 
// Iterative function to set parent nodes for all nodes of the binary tree
// in a given map. The function is similar to the iterative preorder traversal
void setParent(Node* root, unordered_map<int, int> &parent)
{
    // create an empty stack and push the root node
    stack<Node*> stack;
    stack.push(root);
 
    // loop till stack is empty
    while (!stack.empty())
    {
        // Pop the top item from the stack
        Node* curr = stack.top();
        stack.pop();
 
        // push its right child into the stack and set its parent on the map
        if (curr->right)
        {
            parent[curr->right->data] = curr->data;
            stack.push(curr->right);
        }
 
        // push its left child into the stack and set its parent on the map
        if (curr->left)
        {
            parent[curr->left->data] = curr->data;
            stack.push(curr->left);
        }
    }
}
 
// Iterative function to print all ancestors of a given node in a binary tree
void printAncestors(Node* root, int node)
{
    // base case
    if (root == nullptr) {
        return;
    }
 
    // create an empty map to store parent pointers of binary tree nodes
    unordered_map<int, int> parent;
 
    // set the parent of the root node as 0
    parent[root->data] = 0;
 
    // set parent nodes for all nodes of the binary tree
    setParent(root, parent);
 
    // print ancestors of a given node using the parent map
    rootToLeaf(parent, node);
}

int main()
{
    Node* root = nullptr;
 
    /* map of the binary tree in question
         3
       /   \
      /     \
     5       1
    / \     / \
   6   2   0   8
      / \
     7   4
    */
 
    root = new Node(3);
    root->left = new Node(5);
    root->right = new Node(1);
    root->left->left = new Node(6);
    root->left->right = new Node(2);
    root->right->left = new Node(0);
    root->right->right = new Node(8);
    root->left->right->left = new Node(7);
    root->left->right->right = new Node(4);
 
    int node = 8;
    printAncestors(root, node); // prints 1 3 as output
 
    return 0;
}

Space and Time complexity analysis

The time complexity of both recursive and iterative solution is O(n) where n represents the number of nodes in the binary tree.

For space complexity, the recursive solution does not require any extra space to store the nodes but requires space in the call stack (since recursion uses up the call stack). This extra space is equal to the height of the binary tree. Thus the space complexity of the recursive solution is O(h) where h is the height of binary tree.

In the iterative solution, we use an explicit map to store all the nodes in the binary tree. Since there are n nodes in the binary tree, the space complexity of the iterative solution is O(n).